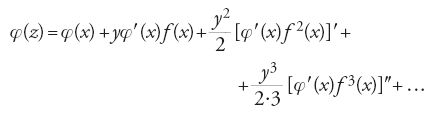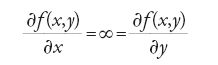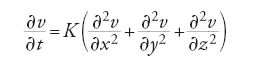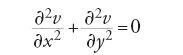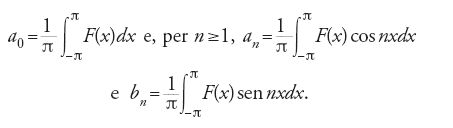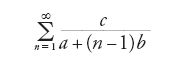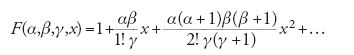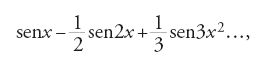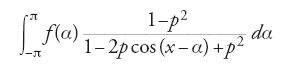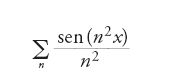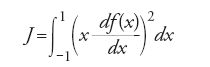L'Ottocento: matematica. Il rigore in analisi

L'Ottocento: matematica. Il rigore in analisi

Il rigore in analisi

L'eredità di Lagrange

All'epoca della Rivoluzione francese, l'esigenza di formare una classe di ingegneri civili e militari aveva convinto il Comité de Salut Public a decretare nel 1794 la creazione di una école Centrale des Travaux Publics, che l'anno seguente prese il nome di école Polytechnique e ben presto divenne la più prestigiosa istituzione scolastica francese. Se il matematico Lazare Carnot (1753-1823), l'organizzatore della vittoria, ne era stato l'ispiratore politico all'interno del Comité, Gaspard Monge (1746-1818), l'inventore della geometria descrittiva, ne era l'animatore dal punto di vista didattico e organizzativo. Non è sorprendente, quindi, che nel programma di studi dell'école la matematica, e inizialmente soprattutto la geometria descrittiva di Monge, avesse un ruolo preponderante. Oltre a Monge, vennero chiamati a insegnarvi matematici quali Joseph-Louis Lagrange (1736-1813) e Sylvestre-François Lacroix (1765-1843), mentre Pierre-Simon de Laplace (1749-1827) faceva parte del Conseil de Perfectionnement che era incaricato della direzione scientifica dell'école. L'importanza di questa scuola per lo sviluppo della matematica fu enorme; la maggior parte dei matematici che assicurarono alla Francia l'egemonia in questo campo fin verso la metà del secolo si formò infatti all'école Polytechnique.

L'insegnamento all'École offrì a Lagrange l'occasione per ripensare i fondamenti del calcolo infinitesimale. Già in un articolo del 1772, pubblicato nelle memorie della Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino, egli aveva indicato nelle linee essenziali un fondamento 'rigorosamente algebrico' del calcolo inventato da Leibniz e Newton. Anche se quell'articolo non aveva avuto seguito nella sua produzione scientifica, certamente l'argomento doveva stargli a cuore se nel 1784 ‒ nel centenario dell'articolo di Leibniz che aveva segnato la nascita del calcolo differenziale ‒ egli aveva convinto l'Accademia di Berlino a bandire un premio per 'una teoria chiara e precisa' dell'infinito in matematica. Tuttavia, il premio non aveva avuto un esito molto soddisfacente. A giudizio dell'Accademia (e, dunque, dello stesso Lagrange in primo luogo) i lavori presentati, compresa la memoria di Simon-Antoine-Jean L'Huillier (1750-1840) che venne alla fine premiata, mancavano tutti della necessaria chiarezza e semplicità, e soprattutto del rigore desiderato. La questione della definizione rigorosa del calcolo rimaneva aperta.

Ricevuta dalla direzione dell'École la richiesta di fornire agli studenti un testo delle sue lezioni, Lagrange pubblicò la Théorie des fonctions analytiques (1797) nella quale riprendeva lo stesso punto di vista anticipato nel 1772. Fin dal sottotitolo della Théorie l'autore dichiarava di non far ricorso a considerazioni su infinitesimi e quantità evanescenti, limiti e flussioni: il calcolo infinitesimale era ridotto all'"analisi algebrica di quantità finite". Sulla base degli sviluppi in serie di potenze delle funzioni note, Lagrange assumeva che una funzione qualunque fosse in generale, ossia salvo al più per valori particolari della x, sviluppabile in serie di potenze

[1] f(x+i)=f(x)+pi+qi²+ri³+…

essendo i una quantità qualunque indeterminata e p,q,r,… funzioni 'derivate' dalla funzione primitiva f(x), indipendenti da i. Dopo qualche ingegnosa manipolazione algebrica (assumendo tacitamente che i fosse abbastanza piccolo) Lagrange mostrava che i coefficienti della [1], cioè le funzioni 'derivate' p,q,r,… erano proprio i coefficienti dello sviluppo in serie di Taylor di f(x), p=f′(x), q=f″(x)/2, r=f‴(x)/2∙3,… e così via. Lo sviluppo

[2] f(x+i)=f(x)+if'(x)+i²f"(x)/2+i³f"'(x)/2∙3…

aveva agli occhi di Lagrange il vantaggio di mostrare come i termini della serie dipendano l'uno dall'altro e "soprattutto, una volta che si sappia ottenere la derivata prima di una funzione qualunque", come si possano ottenere tutti i termini della serie. Il punto delicato però risiede precisamente nel supporre che una funzione qualunque sia sviluppabile nella serie [2], poiché tale sviluppo presuppone l'esistenza delle derivate, che è invece quanto Lagrange cercava di dimostrare. D'altra parte, fin dalle origini del calcolo, il punto cruciale era stato proprio ottenere la derivata prima della funzione. Lagrange doveva essersi reso conto della debolezza dei suoi argomenti se, nella seconda edizione della Théorie (1813), a questo punto aveva aggiunto che, per quanto poco si conoscesse il calcolo differenziale, chiunque poteva vedere che le funzioni derivate p,q,r,… coincidevano con le espressioni df/dx, d²f/dx², d³f/dx³, e così via. Rivelando il circolo vizioso in cui si aggirava il suo ragionamento, Lagrange era costretto ad ammettere che il suo metodo si poteva applicare, in generale, solo a funzioni sviluppabili in serie di potenze di i, perché lo sviluppo [1] potrebbe non aver luogo per una funzione qualsiasi.

La Théorie è un'opera di vasto respiro, la presentazione sistematica dei risultati ottenuti nel corso del secolo, compresi quelli dello stesso Lagrange. Tra i più notevoli vi figurano due risultati che oggi portano il suo nome: la forma del resto della serie di Taylor e lo sviluppo di una funzione in 'serie di Lagrange'. Entrambi i risultati erano di grande interesse per le applicazioni. Lagrange sottolineava infatti che la 'perfezione dei metodi' di approssimazione nei quali si faceva ricorso a serie infinite dipendeva non solo dalla convergenza della serie impiegata, ma anche dalla possibilità di valutare l'errore che si commette trascurando i termini della serie da un certo punto in poi. Quanto alla 'serie di Lagrange', un intero capitolo della Théorie era dedicato alla discussione della 'formula notevole'

che permetteva di sviluppare in serie una funzione 'qualunque' φ(z) dell'incognita z nell'equazione z=x+yf(x), di cui un caso particolare (per f(x)=senx) era la celebre 'equazione di Kepler' di importanza fondamentale in astronomia nello studio del problema dei due corpi.

Dopo la pubblicazione della Théorie Lagrange non perse occasione per sottolineare la radicale originalità della sua concezione 'algebrica' del calcolo, che evitava il 'circuito metafisico degli infinitesimi o dei limiti', come ebbe a dire nel 1799 presentando la teoria delle funzioni analitiche nella seduta inaugurale dei corsi dell'école Polytechnique. Nella sua teoria, affermava Lagrange, regole 'semplici e uniformi' consentivano di passare da una data funzione alle sue funzioni derivate e viceversa. Tali trasformazioni, che dipendevano da operazioni puramente algebriche, corrispondevano alle ordinarie operazioni di derivazione e integrazione. La concezione 'algebrica' di Lagrange permetteva di trattare dallo stesso punto di vista non soltanto i fondamenti del calcolo, ma anche le sue applicazioni alla geometria, alla meccanica e alla teoria delle equazioni differenziali. Quest'ultima era esposta da Lagrange nelle Leçons sur le calcul des fonctions (1801), che rappresentavano un naturale complemento alla Théorie. In particolare egli mostrava che

era una condizione necessaria affinché y=X(x) fosse una soluzione singolare di un'equazione differenziale del primo ordine che, senza perdita di generalità, si poteva sempre scrivere come y′+f(x,y)=0. Lagrange sottolineava con particolare enfasi tale risultato, poiché stabiliva un'intima connessione tra valori 'eccezionali' di una funzione analitica e soluzioni singolari di un'equazione differenziale, permettendo di trattare queste due questioni da un punto di vista unitario, coerente "con la natura stessa delle funzioni derivate".

All'epoca della sua pubblicazione la teoria delle funzioni derivate fu in generale considerata la presentazione più rigorosa del calcolo. Alla teoria di Lagrange si ispirarono opere come il Calcul des derivations (1800) di Louis-François-Antoine Arbogast (1759-1803) e l'Analisi derivata (1802) di Vincenzo Brunacci (1768-1818), professore di calcolo sublime presso l'Università di Pavia. Alle lezioni di Brunacci, raccolte nei quattro volumi del Corso di matematica sublime (1804-1808), si formarono giovani destinati ad avere un ruolo di primo piano nella ricerca matematica italiana della prima metà dell'Ottocento, come Antonio Bordoni (1788-1860), Fabrizio Ottaviano Mossotti (1791-1863) e Gabrio Piola (1791-1850). Mentre Piola era un nobiluomo che coltivava λα μatematica per 'puro spirito filosofico' e Mossotti era stato attratto da ricerche di astronomia teorica prima di essere costretto all'esilio per le sue idee liberali, Bordoni si dedicò soprattutto all'insegnamento, succedendo nel 1816 a Brunacci, del quale condivideva le radicate concezioni lagrangiane.

In Francia, giovani matematici che si erano formati all'école Polytechnique quali Jacques-Frédéric Français e François-Joseph Servois svilupparono le idee di Lagrange in direzione puramente formale, elaborando un originale calcolo degli operatori. In Inghilterra, Charles Babbage, John Herschel e George Peacock, i 'giovani infedeli' che diedero vita all'Analytical Society, trovarono nella teoria di Lagrange un formidabile argomento per la loro critica alla tradizione newtoniana ancora dominante a Cambridge, e al tempo stesso la fonte d'ispirazione per elaborare un originale calcolo degli operatori e tecniche di manipolazione formale di serie infinite.

Tuttavia, la pubblicazione di un certo numero di dimostrazioni 'rigorose' del 'teorema di Taylor' da parte di seguaci o studenti di Lagrange come André-Marie Ampère (1775-1836), répetiteur all'école Polytechnique, o Siméon-Denis Poisson (1781-1840) stava a indicare che affioravano dubbi sul rigore dell'intera costruzione lagrangiana. Nonostante l'autorità del 'primo geometra dell'Impero', come Lagrange era chiamato in epoca napoleonica, a poco a poco divenne chiaro che il suo tentativo di dare una sistemazione rigorosa e definitiva ai fondamenti del calcolo era lontano dall'aver ottenuto successo. Nei primi anni dell'Ottocento la teoria lagrangiana si affiancava alla perdurante pratica leibniziana ed euleriana di ricorrere all'uso di differenziali e infinitesimi, e al metodo dei limiti nel quale, come aveva scritto Jean Le Rond d'Alembert nell'Encyclopédie, risiedeva la 'vera metafisica' del calcolo. Non ragioni metafisiche, ma l'esperienza di insegnamento all'école Polytechnique aveva convinto Lacroix che non c'era via migliore del metodo dei limiti per "conciliare la rapidità di esposizione con l'esattezza del linguaggio", come egli scriveva nel 1810 nella prefazione alla seconda edizione del suo monumentale Traité du calcul différentiel et du calcul intégral, nel quale, aderendo a un sostanziale pluralismo, presentava anche il metodo dei differenziali di Leibniz ed Euler e la teoria lagrangiana. Al Traité, vera e propria summa dell'analisi matematica dell'epoca, era ispirato il manuale che egli adottava a lezione, il Traité élémentaire du calcul différentiel et du calcul intégral (1802) che fu ristampato numerose volte fin oltre la metà dell'Ottocento.

Ben più decisa e radicale era la Réfutation de la théorie des fonctions analytiques de Lagrange di Józef Maria Wroński (1778-1853), singolare figura di matematico estraneo agli ambienti accademici e fondatore del 'messianismo', un movimento filosofico che assunse i caratteri di una vera e propria setta religiosa basata sulla rivelazione di un 'Assoluto' universale e razionale. Pur rivestite da motivazioni filosofiche scarsamente convincenti, le critiche di Wroński erano tuttavia acute e penetranti e rivelavano il circolo vizioso che stava alla base della teoria di Lagrange, tanto da provocare un'immediata risposta di Poisson, che pubblicava una nuova "rigorosa dimostrazione della serie e del teorema di Taylor", giudicata a sua volta da Wroński solo una petitio principii. Ormai il favore con cui era stata accolta la teoria lagrangiana stava venendo meno rapidamente. Ben più significativo delle critiche di Wroński, era il fatto che Laplace, in un articolo sulle funzioni generatrici letto all'Institut de France nel 1811, passando in rassegna i più recenti progressi nel calcolo, non aveva speso una parola per la teoria del suo illustre collega che, all'epoca, non era più neppure insegnata all'école Polytechnique.

Le serie di Fourier

All'inizio dell'Ottocento era diffusa l'opinione che la miniera della matematica fosse ormai prossima a esaurirsi e che, se non si fossero trovati nuovi filoni di ricerca, sarebbe stato necessario prima o poi abbandonarla. Questa convinzione, che Lagrange aveva confidato in una lettera a d'Alembert fin dal 1781, era espressa con ben diversa ufficialità nel Rapport historique sur le progrès des sciences mathématiques depuis 1799 et leur état actuel (1810) che Jean-Baptiste-Joseph Delambre (1749-1822), segretario perpetuo dell'Institut de France, aveva scritto su richiesta di Napoleone. Dopo aver esaltato i grandi successi ottenuti da Monge, Lagrange e Laplace nei vari campi della matematica, Delambre concludeva affermando che sarebbe stato avventato cercare di prevedere quali chances di sviluppo riservava il futuro. Le teorie che erano maggiormente progredite nel corso del secolo precedente si erano imbattute in 'difficoltà insormontabili', e sembrava che la 'potenza dell'analisi' fosse ormai 'praticamente esaurita'. La perfezione nei 'dettagli' sembrava la sola cosa che si potesse affrontare con successo. Nondimeno, Delambre auspicava che "lo spettacolo dell'analisi e della meccanica del nostro tempo" esortasse le generazioni future a non vedere "niente di impossibile in ciò che resta da fare".

Tra i 'dettagli', che secondo Delambre restavano da perfezionare, c'erano i fondamenti del calcolo infinitesimale, questione che la Théorie aveva lasciata aperta e che si intrecciava con l'analoga questione dei fondamenti della meccanica. Nella Méchanique analitique (1788) Lagrange si era largamente servito del linguaggio degli infinitesimi, a cominciare dalla formulazione del principio delle velocità virtuali, una 'specie di assioma' di tutta la meccanica. Tra la fine del Settecento e i primi anni del nuovo secolo diverse dimostrazioni di quel 'principio' erano state proposte dallo stesso Lagrange, da Gaspard-François-Clair-Marie Riche de Prony, professore di meccanica all'école e da Jean-Baptiste-Joseph Fourier, répétiteur all'école. Quel principio era oggetto di lavori di Louis Poinsot e di Lazare Carnot, che ne discuteva nei suoi Principes fondamentaux de l'équilibre et du mouvement (1803), mentre Ampère ne dava una 'nuova dimostrazione' in termini di funzioni derivate. Lo stesso Lagrange, tuttavia, non aveva ritenuto necessario riscrivere la Méchanique analytique nel linguaggio delle funzioni derivate, e pubblicando la seconda edizione del suo trattato nel 1811 manteneva invece la notazione differenziale, adottata nel 1788.

Più che le discussioni sui fondamenti della meccanica, furono problemi di carattere fisico-matematico a offrire le motivazioni per inaspettati sviluppi dell'analisi. Nel 1807 Fourier presentò all'Institut una memoria, che inaugurava un campo di ricerche completamente nuovo, lo studio matematico della propagazione del calore nei corpi. L'opera di Newton, osservava Fourier, aveva consentito di trovare le leggi che regolano l'intero 'sistema del mondo', come aveva mostrato Laplace, e tuttavia non permettono di spiegare i fenomeni che si osservano come 'effetti del calore'. L'argomento, di grande interesse dal punto di vista pratico e teorico, era stato oggetto di ricerche da parte di Laplace e di Antoine-Laurent Lavoisier (1743-1794) che nel 1784 avevano determinato il calore specifico di varie sostanze. In seguito Jean-Baptiste Biot (1774-1862), allievo di Laplace, aveva pubblicato nel 1804 un lavoro sulla propagazione del calore e attirato l'attenzione di Fourier sull'argomento. Nel suo lavoro Fourier forniva l'equazione differenziale alle derivate parziali che descrive la propagazione del calore nei corpi

(dove v, la temperatura, è una funzione delle coordinate x, y, z e del tempo t e K è una costante che dipende da caratteristiche fisiche del corpo come conducibilità e densità), e la integrava in alcuni casi particolari, ricorrendo allo sviluppo delle soluzioni in serie trigonometriche. L'uso di tali serie, già presente, nel 1752, nel lavoro con cui Daniel Bernoulli era intervenuto nella polemica sulle corde vibranti, incontrò tuttavia obiezioni dal punto di vista del rigore soprattutto da parte di Lagrange. A suo parere, infatti, funzioni 'qualunque' come quelle che provenivano dalla soluzione di equazioni differenziali erano rappresentabili in serie di potenze, e non in serie di seni e coseni di archi multipli, come pretendeva invece Fourier. L'importanza della questione convinse l'Institut a fare della propagazione del calore argomento di un premio per il 1811, che fu attribuito a una nuova memoria presentata da Fourier. Anche questa volta, tuttavia, la commissione giudicatrice (di cui faceva parte Lagrange) avanzò riserve "per quanto riguarda la generalità e il rigore" dei metodi usati da Fourier nell'integrazione delle equazioni differenziali alle derivate parziali. Così, contrariamente all'uso, la memoria vincitrice non fu pubblicata, e apparve a stampa solo nel 1824, quando Fourier era ormai divenuto segretario perpetuo dell'Académie des Sciences, ripristinata dopo la Restaurazione del 1815.

I risultati e i metodi di Fourier erano comunque ben noti negli ambienti matematici parigini. Poisson aveva pubblicato un ampio resoconto della sua prima memoria del 1807 e aveva egli stesso trattato il tema della propagazione del calore in numerose note apparse a partire dal 1809. Per integrare le equazioni differenziali ottenute egli si serviva dei metodi 'classici': sviluppi in serie di potenze, soluzioni funzionali, funzioni speciali, e anche serie trigonometriche secondo l'uso che ne aveva fatto Lagrange in una lontana memoria sulle corde vibranti. Queste ricerche di Poisson, all'origine del suo volume Théorie mathématique de la chaleur (1835), si intrecciavano con i contemporanei lavori di Fourier rimasti perlopiù inediti, sollevando tra i due accese rivalità e discussioni, cui prese parte anche Augustin-Louis Cauchy (1789-1857), un giovane ingegnere uscito dall'école Polytechnique, che aveva trascorso qualche tempo lavorando alla costruzione del porto di Cherbourg prima di tornare a Parigi e dedicarsi interamente alla carriera accademica. Cauchy si era ben presto segnalato negli ambienti matematici parigini, vincendo il premio bandito dall'Institut per il 1815 con una memoria sulla teoria della propagazione delle onde sulla superficie di un fluido in cui si ritrovavano molte delle formule di cui si era servito anche Fourier. Questi, eletto segretario perpetuo dell'Académie nel 1822, diede allora alle stampe la Théorie analytique de la chaleur (1822), una vera e propria miniera di scoperte matematiche e un testo paradigmatico per la ricerca scientifica, come dirà nel 1829 Auguste Comte.

Il Discours préliminaire, premesso alla Théorie, aveva un aperto carattere programmatico. "'Le cause prime' dei fenomeni naturali ci sono sconosciute" ‒ affermava Fourier ‒ "ma sono soggette a leggi semplici e costanti che possono essere scoperte dall'osservazione" (1822, p. XV) e sono espresse sotto forma di equazioni differenziali. Anche gli effetti del calore sono soggetti a leggi costanti che soltanto il ricorso all'analisi matematica consente di scoprire. Così, le questioni fisiche relative alla propagazione del calore si riducono a "problemi di analisi pura, che costituisce l'oggetto vero e proprio della teoria". Secondo Fourier, "lo studio profondo della Natura è la fonte più feconda di scoperte matematiche. Offrendo un oggetto di ricerca ben determinato, questo studio ha non solo il vantaggio di escludere questioni vaghe e calcoli senza scopo, ma è anche un metodo sicuro per sviluppare la stessa analisi" il cui dominio, ai suoi occhi, era "tanto ampio quanto la stessa Natura".

Le serie trigonometriche si affacciavano già nella soluzione del semplice caso di una lamina rettangolare di lunghezza infinita a temperatura stazionaria. In questo caso l'equazione [5] si riduce alla più semplice equazione

soggetta a opportune condizioni iniziali. Dopo un vero e proprio tour de force analitico, che includeva la risoluzione di un sistema di infinite equazioni lineari in infinite incognite con una specie di induzione e la felice divinazione del risultato di un ardito procedimento di limite, Fourier era in grado di determinare i coefficienti della serie. Da qui egli concludeva che una qualunque funzione, anche discontinua, poteva essere rappresentata con la serie trigonometrica (che oggi porta il suo nome)

dove

Studiando la propagazione del calore lungo un filo rettilineo di lunghezza infinita, egli mostrava poi che una funzione poteva essere rappresentata anche sotto forma di integrale (di Fourier)

e spiegava in quale modo si poteva passare da una rappresentazione all'altra.

Agli occhi di Fourier, i propri risultati sulle serie trigonometriche liberavano da ogni difficoltà l'analisi del problema delle corde vibranti realizzata precedentemente da Daniel Bernoulli e ne giustificavano le conclusioni, che il 'celebre Euler' (e con lui Lagrange) aveva sempre rifiutato.

Ci si chiede cosa intendesse Fourier parlando di discontinuità di una curva o di una funzione. In generale egli sembra condividere la definizione euleriana secondo cui una curva è continua quando è rappresentata da un'unica espressione analitica, ed è discontinua quando le sue diverse parti sono rappresentate da differenti funzioni. In alcuni passi tuttavia egli sembra avere in mente una concezione che corrisponde a quella 'moderna', e altrettanto moderna è la sua insistenza sul fatto che una funzione può essere definita 'a tratti' e rappresentata da una serie trigonometrica convergente in un certo intervallo e divergente, oppure convergente a un'altra funzione, fuori dall'intervallo. Quanto alla convergenza delle sue serie, Fourier cerca in generale di stabilirla calcolando la somma di un certo numero di termini della serie. Tale somma mostra quale debba essere il limite quando il numero dei termini cresce indefinitamente, e Fourier confida che la natura fisica dei problemi assicuri la convergenza delle serie e gli eviti di avventurarsi in 'questioni vaghe e calcoli senza scopo'. Nonostante le perentorie affermazioni di Fourier, il problema della convergenza delle serie che portano il suo nome e, più in generale, l'analisi delle questioni analitiche che a esse sono legate, costituirà uno dei temi di ricerca più fecondi e, per oltre un secolo, una specie di filo rosso che collega alcuni tra i capitoli più difficili e più delicati dell'analisi matematica.

Negli anni Venti dell'Ottocento intorno alla figura di Fourier si raccolse un gruppo di giovani intellettuali e matematici come Joseph Liouville (1809-1882), studente dell'école Polytechnique e poi, dal 1838, professore alla stessa École; Charles-François Sturm (1803-1855), uno svizzero che dal 1825 si era stabilito a Parigi divenendo grande amico di Liouville e poi suo collega di insegnamento all'École Polytechnique; Peter Gustav Lejeune Dirichlet (1805-1859), un prussiano allora a Parigi per un periodo di studio; infine, Comte, il filosofo del positivismo, che dedicherà a Fourier il suo Cours de philosophie positive, condividendo il 'programma' delineato nelle pagine iniziali della Théorie. Alle concezioni di Fourier, largamente condivise tra i matematici francesi formatisi all'École Polytechnique, si opponeva agli inizi degli anni Trenta l'opinione di Carl Gustav Jacob Jacobi (1804-1851), un giovane matematico destinato a diventare uno dei protagonisti della ricerca matematica in Germania. Sensibile alle correnti neoumanistiche dominanti fra i matematici tedeschi, che concepivano la loro scienza come ricerca di verità astratte e formali, condotta per il puro piacere dello spirito, in un celebre passo di una lettera ad Adrien-Marie Legendre (1752-1833) Jacobi scriveva: "È vero che il signor Fourier era dell'opinione che lo scopo principale delle matematiche fosse l'utilità pubblica e la spiegazione dei fenomeni naturali; ma un filosofo come lui avrebbe dovuto sapere che lo scopo della scienza è l'onore dello spirito umano e che, da questo punto di vista, una questione di teoria dei numeri vale tanto quanto una relativa al sistema del mondo" (Jacobi 1881-91, I, p. 454). Una contrapposizione di concezioni che nella sostanza si ripresenterà irrisolta nello sviluppo dell'analisi dell'Ottocento.

Nuovi criteri di rigore

Quando Cauchy entrò all'École Polytechnique, nel novembre 1805, il programma del corso di analisi non menzionava neppure la teoria lagrangiana delle funzioni derivate, ma richiedeva invece che la nozione di differenziale si fondasse sulla teoria dei limiti. Questa stessa teoria occupa un posto centrale nel Cours d'analyse, il testo che Cauchy diede alle stampe nel 1821 quando era a sua volta diventato professore all'École. Il Cours divenne ben presto una sorta di manifesto della 'moderna analisi', come la chiamava lo stesso Cauchy; "un libro che deve essere letto da ogni analista che ama il rigore nelle ricerche matematiche", scrisse nel 1826 il giovane norvegese Niels Henrik Abel (1802-1829), che ne fece la propria bibbia matematica.

Fin dall'introduzione al Cours Cauchy esprimeva con grande chiarezza le proprie concezioni sul rigore da adottare in analisi: "Quanto ai metodi ‒ scriveva in un passo diventato celebre ‒ ho cercato di conferir loro tutto il rigore che si esige in geometria in modo da non ricorrere mai ad argomenti tratti dalla generalità dell'algebra" (Cauchy 1821a, p. 2) tanto cara a Lagrange. La Théorie des fonctions analytiques era stata una delle opere più studiate dal giovane Cauchy. Con Lagrange egli concordava sulla necessità di fondare il calcolo infinitesimale, senza limitarsi a giustificarne i metodi con il successo nelle applicazioni, dissentiva però apertamente dai suoi argomenti di natura algebrica, che venivano liquidati come "induzioni" capaci occasionalmente di "far presentire la verità", ma poco in accordo "con l'esattezza tanto vantata delle scienze matematiche". Cauchy vi contrapponeva l'esigenza di rigore 'euclideo', anche a costo di limitare "l'estensione indefinita" attribuita alle formule algebriche, e di dover "ammettere diverse proposizioni che sembreranno forse un po' dure a prima vista", come il fatto che "una serie divergente non ha somma". Quando si considerava una serie, bisognava anzitutto accertarsi della sua convergenza.

Nonostante l'enfasi postavi da Cauchy, la sua affermazione non era nuova. In più luoghi Euler aveva apertamente dichiarato che "le serie divergenti non hanno somma propriamente detta". Egli stesso aveva dimostrato nel 1734 che la serie armonica generalizzata

è divergente, anche se il termine generico tende a zero. Tuttavia egli non aveva esitato a manipolare serie divergenti per ottenere nuovi risultati, come la formula

dove C=0,57721… è la costante di Eulero-Mascheroni. Quando si tratta di serie infinite, egli aveva affermato nelle Institutiones calculi differentialis (1755), "tutta la difficoltà sta nel termine 'somma'". Per aggirare difficoltà e apparenti contraddizioni Euler aveva proposto una nuova definizione, chiamare cioè somma di una serie "l'espressione finita dal cui sviluppo origina la serie". Una definizione in accordo con quella usuale per le serie convergenti, e che non reca alcun incomodo per le serie divergenti perché esse non hanno somma. Questo punto di vista divenne a poco a poco dominante nella seconda metà del Settecento. Secondo Lagrange, per esempio, si doveva poter 'sempre' sostituire alla serie geometrica l'espressione 1/1−x anche se quest'ultima era "realmente uguale" alla somma della serie solo per x minore di 1. A suo parere, "contestare l'esattezza di una tale sostituzione", come farà Abel, significava "stravolgere i più comuni principî dell'analisi". Quegli stessi principî che egli porrà alla base della Théorie des fonctions analytiques. Come spiegava Bernoulli nel 1771 parlando di serie ricorrenti divergenti, attribuire una somma a una tale serie era "manifestamente falso in concreto, e tuttavia non assurdo in abstracto". Se dunque l'affermazione di Cauchy non era in sé nuova, del tutto nuove erano invece le conseguenze che egli traeva: di rifiutare la distinzione tra l'aspetto formale e quello numerico conferendo legittimità solo a quest'ultimo, e quindi bandire dall'analisi le serie divergenti. Alle stesse conclusioni era giunto Carl Friedrich Gauss (1777-1855) quando, giovanissimo, aveva cominciato a occuparsi di serie infinite, annotando i risultati ottenuti nel suo diario. Nel 1805 egli aveva affrontato il problema della convergenza della serie ipergeometrica

ottenuta da Euler come integrale di un'equazione differenziale lineare del secondo ordine e nel 1813 aveva pubblicato i risultati ottenuti. La [12] era una serie di grande generalità. Gauss aveva osservato che al variare dei parametri α,β,γ essa poteva rappresentare funzioni algebriche, come la somma della serie del binomio, o funzioni trascendenti, come le funzioni trigonometriche o quella logaritmica e trascendente di ordine superiore. Tuttavia, "per sua natura" la ricerca doveva essere limitata "ai casi in cui la serie effettivamente converge", ossia per ∣x∣⟨1, come Gauss stabiliva facilmente mediante il criterio di d'Alembert, mentre è divergente per ∣x∣>1 e "la sua somma non può essere espressa". Quando ∣x∣=1 egli stabiliva "con rigore geometrico" che la serie era convergente se e solo se γ−α−β>0. Una serie non sempre convergente come questa, scriveva all'amico Friedrich Wilhelm Bessel (1784-1846), "può essere presa come una definizione solo entro i limiti in cui converge" (Gauss 1863-1933, X, 1, p. 363). In conclusione del suo lavoro, sottolineando "la cura necessaria nel trattare quantità infinite", Gauss affermava che queste ultime potevano essere ammesse in matematica "solo in quanto potevano esser ridotte alla teoria dei limiti".

Anche per Cauchy lo strumento essenziale per introdurre le nozioni fondamentali dell'analisi era il concetto di limite, che così definiva: "allorché i valori successivamente assunti da una stessa variabile si avvicinano indefinitamente a un valore fissato in modo da differirne alla fine tanto poco quanto si vuole, quest'ultima quantità è chiamata il limite di tutte le altre" (Cauchy 1821a, p. 4). In termini di limiti si potevano definire in maniera precisa controverse nozioni come quella di infinito (una variabile i cui "valori numerici crescono sempre di più in modo da superare ogni numero dato") e quella di infinitesimo (una variabile "che ha zero come limite"), per mezzo della quale Cauchy precisava poi il fondamentale concetto di continuità di una funzione in un intervallo (quando "un incremento infinitesimo della variabile produce un incremento infinitesimo della funzione stessa").

Lontano da Parigi e con ogni evidenza all'insaputa di Cauchy, una definizione del tutto simile di continuità di una funzione era stata pubblicata nel 1817 negli atti della Società delle Scienze di Praga dal monaco boemo Bernhard Bolzano (1781-1848). Contrariamente a Cauchy, Bolzano aveva intrapreso nel 1810 una rigorosa analisi critica dei concetti fondamentali della matematica animato da esigenze filosofiche. Il suo lavoro del 1817 aveva per oggetto la dimostrazione di un teorema di immediata evidenza geometrica: una funzione continua su un intervallo, che assume valori di segno opposto agli estremi, deve annullarsi almeno in un punto dell'intervallo. In termini geometrici, una curva continua non può passare da una parte all'altra dell'asse x senza tagliarlo almeno in un punto. Un fatto che era stato assunto come del tutto evidente da Gauss nella sua dimostrazione del teorema fondamentale dell'algebra (1799), ma che, per essere accettato, necessitava secondo Bolzano di una dimostrazione puramente analitica. A tale scopo egli si serviva non soltanto di considerazioni sulle serie infinite, che aveva già anticipato in un opuscolo sul teorema del binomio, ma anche della distinzione tra elemento massimo e estremo superiore di un insieme di numeri reali ‒ concetto questo del tutto nuovo da lui introdotto, la cui importanza fondamentale in analisi si rivelerà qualche decennio più tardi con l'opera di Karl Theodor Wilhelm Weierstrass.

Come la definizione di continuità, anche la condizione necessaria e sufficiente per la convergenza delle serie stabilita da Bolzano era del tutto simile a quella che sarà enunciata da Cauchy nel Cours. Dopo aver definito la somma di una serie come il limite cui "si avvicina indefinitamente" la somma dei primi n termini al crescere indefinitamente di n, Cauchy mostrava che una condizione necessaria e sufficiente (oggi detta 'di Cauchy') per stabilire la convergenza di una data serie è che per valori crescenti di n, le somme parziali dei primi n, n+1, n+2,… termini della serie differiscano tra loro per quantità infinitesime. Un'immediata applicazione di tale criterio era il seguente teorema: data una serie di funzioni di una variabile, continue nell'intorno di un particolare valore della variabile per il quale la serie è convergente, la somma della serie è anch'essa una funzione continua nell'intorno di quel valore particolare. Questo teorema, su cui appunterà le sue critiche Abel, giocava un ruolo decisivo nella dimostrazione dello sviluppo in serie del binomio, con cui si conclude la prima parte del Cours d'analyse. La seconda parte era dedicata alle variabili complesse e alle funzioni di quelle variabili, e culminava nella dimostrazione del teorema fondamentale dell'algebra. Come quella di Gauss, anche la dimostrazione di Cauchy si basava su un argomento di continuità da lui ritenuto del tutto evidente.

L'analisi algebrica costituiva la premessa alle lezioni sul calcolo infinitesimale vero e proprio, che Cauchy pubblicò nel 1823 nel Résumé des leçons […] sur le calcul infinitesimal. "Il mio scopo ‒ affermava Cauchy ‒ è stato quello di conciliare il rigore, che mi ero posto come norma irrinunciabile nel Cours d'analyse, con la semplicità che proviene dalla considerazione diretta degli infinitesimi". Denunciando ancora una volta l'insufficienza del 'metodo delle serie' adottato da Lagrange per fondare il calcolo, Cauchy obiettava che "malgrado tutto il rispetto che si deve a una grande autorità, la maggior parte dei geometri oggi concorda nel riconoscere l'incertezza dei risultati ai quali si può essere portati usando le serie divergenti". In particolare, Cauchy aveva scoperto casi in cui la serie di Taylor "sembra fornire lo sviluppo di una funzione in serie convergente, sebbene la somma della serie differisca in maniera essenziale dalla funzione proposta" (Cauchy 1823b, p. 2). Questo era il sorprendente risultato cui era giunto nel 1821 considerando la funzione f(x)=e^-1/x2, le cui derivate sono tutte nulle per x=0, e che si era affrettato a presentare all'Académie e a pubblicare in una nota apparsa nel "Bulletin de la Société Philomatique". Per studiare le proprietà di una funzione, osservava Cauchy, era pratica diffusa, anche tra chi non condivideva il punto di vista fondazionale di Lagrange, quella di servirsi del suo sviluppo in serie, nella tacita ipotesi che la funzione fosse completamente caratterizzata da tale sviluppo. Il caso tipico era la serie di Maclaurin (che si ottiene dalla [2] ponendo x=0); l'esempio di Cauchy mostrava che le cose non stavano in questo modo. Alla successione infinita di valori f(0), f′(0), f″(0),… potevano corrispondere funzioni differenti, come f(x)=e^-1/x2, g(x)=e^−1/x,… e viceversa, differenti funzioni potevano avere lo stesso sviluppo in serie come accadeva con f(x)=e^-x2, e g(x)=e^−x2, il cui sviluppo coincideva con quello della sola e^−x2. In definitiva, lo sviluppo in serie di potenze di una funzione f(x) poteva considerarsi equivalente alla funzione se e soltanto se la serie era convergente, e la sua somma era proprio f(x).

Nella stessa occasione, con l'esempio dy=[1+(y−x)log(y−x)]dx Cauchy 'falsificava', come si direbbe oggi, la condizione necessaria stabilita da Lagrange per determinare una soluzione singolare di un'equazione differenziale del prim'ordine. La funzione y=x, osservava Cauchy, soddisfa la condizione di Lagrange, eppure non è una soluzione singolare, ma una soluzione particolare compresa nell'integrale generale log(y−x)=ce^x. Tali considerazioni avevano convinto Cauchy a presentare i principî del calcolo differenziale senza ricorrere alle serie. Come spiegava nell'avvertenza al Résumé, egli si era "visto costretto a rinviare al calcolo integrale la formula di Taylor" che poteva essere ammessa "solo finché la serie che vi è contenuta sia limitata a un numero finito di termini e completata con un integrale definito".

Nelle pagine del Résumé Cauchy introduceva la nozione di derivata di una funzione come il limite del rapporto incrementale f(x+α)−f(x)/α, dove α è un infinitesimo. Anche il concetto di differenziale dy di una funzione y=f(x) era definito mediante un opportuno limite. Nella concezione di Lagrange, che riprendeva una pratica consolidata fin dalle origini del calcolo, l'integrazione di una funzione f(x) era la ricerca di una funzione "primitiva" F(x) tale che la sua "funzione derivata" F′(x) fosse la funzione f(x) di partenza. Il teorema fondamentale del calcolo consentiva poi di introdurre il concetto di integrale definito ∫^b_a f (x)dx mediante la formula ∫^b_a f (x)dx=F(b)-F(a) dove F′(x)=f(x).

Al contrario, secondo il parere di Cauchy, era "necessario dimostrare generalmente l'esistenza degli integrali o funzioni primitive" prima di mostrare le loro proprietà, e allo scopo "era indispensabile" anzitutto "stabilire la nozione di integrale preso entro limiti dati, o integrale definito" (Cauchy 1823b, p. 4). Data una funzione f(x) continua su un intervallo [x₀, X] Cauchy considerava una suddivisione arbitraria dell'intervallo in n parti e la somma S dei prodotti

[13] S=(x₁-x₀)f (x₀)+(x₂-x₁)f(x₁)+…+(X-x_n-1)f(x_n-1)

che dipendeva dal numero n e dal modo di suddivisione dell'intervallo. Cauchy mostrava che se il numero n degli intervalli della suddivisione diventa "molto grande", in modo che l'ampiezza di ciascuno di essi sia arbitrariamente piccola, il valore di S, al crescere indefinitamente di n, "finirà per essere sensibilmente costante", ossia "finirà per raggiungere un certo limite, che dipenderà unicamente dalla forma della funzione f(x) e dai valori degli estremi x₀, X" (ibidem, 125). Tale limite era l'integrale definito; queste erano le conclusioni cui perveniva Cauchy.

Egli non aveva difficoltà a mostrare che S(x), con x variabile, era, a meno di una costante, l'integrale indefinito della funzione, e a estendere poi la sua definizione al caso di funzioni discontinue in un numero finito di punti. In questo rovesciamento di prospettiva, nella sua insistenza sulla necessità di "dimostrare generalmente l'esistenza" degli integrali indefiniti consisteva la grande novità teorica introdotta da Cauchy. Secondo questa stessa impostazione egli affrontava il problema dell'integrazione delle equazioni differenziali durante il corso per gli studenti del secondo anno. Egli mostrava come risolvere il cosiddetto "problema di Cauchy" nel caso di un'equazione differenziale della forma dy=f(x,y)dx con la condizione per la soluzione y(x) di soddisfare dati valori iniziali x₀, y₀ nell'intorno dei quali f(x,y) e ∂f/∂y erano supposte continue. La dimostrazione dell'esistenza e unicità della soluzione in un intorno di x₀, y₀ era condotta da Cauchy con il 'metodo di approssimazione', del tutto analogo a quello introdotto nella definizione del concetto di integrale definito. Cauchy aveva iniziato a dare alle stampe le sue lezioni, ma interruppe bruscamente la pubblicazione quando la direzione dell'École lo rimproverò di perder tempo a discutere astruse questioni di rigore ‒ un "lusso d'analisi" sconsigliabile, se non controproducente, per dei futuri ingegneri ‒ invece di dedicarsi alle applicazioni del calcolo differenziale.

Sulle orme di Cauchy

"Mi sembra che questo teorema ammetta delle eccezioni", scriveva Abel in un articolo del 1826, commentando il teorema di Cauchy sulla continuità della somma di una serie convergente di funzioni continue. Per esempio, la somma della serie di funzioni continue

è discontinua per x=(2m+1)π, con m intero. L'esempio era già noto a Euler, ed era stato oggetto di discussioni tra Fourier e Lagrange. "Ci sono, come si sa, diverse serie di questo tipo", aggiungeva Abel che, con ogni probabilità, l'aveva appreso dalla lettura della Théorie analytique de la chaleur. In quell'articolo, dedicato alla dimostrazione del teorema del binomio per esponenti complessi, Abel provava due notevoli teoremi sulle funzioni continue. Con il primo stabiliva le condizioni che rendevano rigoroso un procedimento assai diffuso per calcolare la somma delle serie numeriche, quello di trasformare la serie data in una serie di potenze di x, calcolarne la somma e poi sostituire in quest'ultima al posto della x il particolare valore che dava la serie di partenza. Procedimento legittimo, affermava Abel, soltanto se questo particolare valore apparteneva al dominio di convergenza della serie. Il secondo teorema riguardava le serie convergenti di funzioni continue. L'intento era di sostituire al teorema 'con eccezioni' di Cauchy un enunciato sicuro, ma di portata più limitata. Tuttavia, come era accaduto nel caso della dimostrazione di Cauchy, anche quella di Abel sarebbe stata oggetto di analoghe critiche dal punto di vista del rigore.

La serie [14] era solo un caso particolare delle serie trigonometriche che Fourier aveva sistematicamente utilizzato nell'integrazione delle equazioni differenziali. I suoi metodi tuttavia erano lontani dal soddisfare i criteri di rigore stabiliti da Cauchy. Il compito di provare "in maniera precisa e rigorosa" i suoi risultati era reso ancor più urgente dal fatto che, come aveva osservato Poisson fin dal 1820, ci si imbatteva a ogni passo in tali serie quando si applicava l'analisi a questioni di fisica o di meccanica. Poisson aveva proposto una dimostrazione basata sulla considerazione dell'integrale (che oggi porta il suo nome)

quando p tende a 1 e x tende a α. Con disinvolte manipolazioni, ricorrendo tra l'altro al procedimento di sostituzione che sarà criticato da Abel, egli riusciva infine a mostrare che, dopo opportune trasformazioni, dalla [15] si otteneva la rappresentazione in serie di Fourier completa della f(x). I ragionamenti di Poisson erano giudicati poco rigorosi da Cauchy, che nel 1827 propose a sua volta due diverse dimostrazioni della convergenza delle serie di Fourier. La prima si basava su un 'criterio di convergenza' che due anni più tardi sarà confutato da Dirichlet con un semplice esempio; la seconda ‒ ottenuta come applicazione di metodi di analisi complessa (la teoria dei residui dello stesso Cauchy) ‒ passò del tutto inosservata.

La delicata questione della convergenza delle serie di Fourier fu affrontata con il necessario rigore da Dirichlet nel 1829. Memore di quanto aveva spiegato Cauchy con il celebre esempio della funzione f(x)=e-^1/x2, Dirichlet sosteneva che la via seguita nel suo lavoro avrebbe portato a stabilire la convergenza di queste serie e a determinare nello stesso tempo il loro valore. La memoria di Dirichlet è un gioiello di letteratura matematica, un esempio paradigmatico dei nuovi standard di rigore che, sull'esempio di Cauchy, si stavano imponendo in analisi nei primi decenni dell'Ottocento. Dopo un accurato esame dei casi che si possono presentare, Dirichlet riuscì a individuare condizioni sufficienti per la rappresentabilità di una funzione f(x) in serie di Fourier convergente all'interno dell'intervallo [−π, π]. Nell'ipotesi che la funzione sia continua, o al più discontinua in un numero finito di punti, e presenti un numero finito di massimi e minimi, lo sviluppo in serie di Fourier di f(x) converge a (1/2) [f(x+ε)+f(x−ε)], dove ε è un infinitesimo.

Nel tentativo di indebolire ulteriormente le ipotesi del teorema, Dirichlet considerava la funzione, che oggi porta il suo nome, con un'infinità di punti di discontinuità

dove c e d sono costanti diverse tra loro. Si tratta di una funzione che ha "valori finiti e determinati" per ogni valore di x, osservava Dirichlet, eppure "non sarebbe possibile sostituirla nella serie". Infatti, gli integrali che esprimono i coefficienti della serie [8] "perderebbero in questo caso ogni significato".

La seconda condizione sul numero di massimi e minimi della funzione si era imposta nel corso della dimostrazione, e Dirichlet riteneva che fosse più che altro legata alla particolare procedura dimostrativa seguita. Così, quando Gauss gli scrisse nel 1853 ipotizzando la possibilità di estendere la dimostrazione al caso di funzioni con un numero infinito di oscillazioni, Dirichlet rispose che tale supposizione gli pareva "completamente confermata" se si voleva "in qualche modo prescindere da certi casi del tutto singolari". Uno di questi casi "singolari" sarà reso noto nel 1876 da Paul Du Bois-Reymond (1831-1889) con l'esempio di una funzione continua, la cui serie di Fourier non converge in punti isolati.

Il lavoro di Dirichlet confermava quello che Abel aveva intuito: le serie di Fourier potevano rappresentare funzioni discontinue, contraddicendo il teorema che Cauchy aveva enunciato nel suo Cours d'analyse e ripetuto nei Résumés analytiques delle lezioni tenute a Torino. Dal 1830, dopo la Rivoluzione di Luglio e la cacciata di Carlo X di Borbone, anche Cauchy, realista convinto, aveva lasciato la Francia e si era stabilito per qualche tempo in Italia, accettando la cattedra che gli era stata offerta da Carlo Alberto. Il soggiorno di Cauchy suscitò vivaci reazioni negli ambienti matematici del nostro paese, largamente influenzati dalle idee di Lagrange. Non senza contrasti, a Torino Cauchy presentò all'Accademia delle Scienze una memoria su un suo nuovo "calcolo dei limiti", con il quale era riuscito non solo a stabilire "principî generali e di facile applicazione" sullo sviluppo in serie delle funzioni, ma anche a "dimostrare con rigore le formule indicando le condizioni della loro esistenza, e fissare inoltre i limiti degli errori che si commettono trascurando i resti che devono completare le serie". Da qui il nome del suo 'calcolo'. In tale memoria, tradotta e pubblicata in italiano nel 1832 a cura di Piola, Cauchy discuteva quando una funzione f(x) può essere sviluppata in serie di potenze di x, convergente per tutti i valori il cui modulo è minore di quelli per cui la funzione o la sua derivata cessano di essere finite e continue. Il 'calcolo dei limiti' (o metodo dei maggioranti, come si dice oggi) consentiva di maggiorare il resto della serie, valutando così l'errore che si commetteva nei calcoli (quelli astronomici in particolare) quando ci si arrestava a un dato termine della serie. Si trattava di un metodo che rivelerà tutta la sua potenza e fecondità nei lavori di analisi complessa, ai quali Cauchy si dedicò soprattutto dopo il suo ritorno a Parigi nel 1838.

Proprio commentando un lavoro di Charles-Auguste Briot (1817-1882) e Jean-Claude Bouquet (1819-1885) sulle serie a termini complessi, Cauchy trovò nel 1853 l'occasione per ritornare sul suo controverso teorema relativo alla somma di una serie convergente di funzioni continue. Dopo aver osservato che il teorema valeva per le serie di potenze, Cauchy riconosceva che l'enunciato richiedeva delle restrizioni 'per altre serie'. Senza citare Abel, egli considerava l'esempio [14] e affermava che "è facile vedere come deve essere modificato l'enunciato del teorema, perché non si presenti più alcuna eccezione". Modifiche analoghe erano state proposte da qualche anno. In un articolo del 1848 Philipp Seidel (1821-1896), che aveva seguito i corsi di Dirichlet a Berlino, aveva osservato che nella dimostrazione di Cauchy si celava l'"ipotesi nascosta" che in corrispondenza di un incremento infinitesimo della variabile x, anche la variazione del resto r_n(x) della serie fosse 'trascurabile' per n sufficientemente grande e per ogni x. Da parte sua, Seidel mostrava che se una serie di funzioni continue rappresenta una funzione discontinua, allora per valori di x "nell'intorno immediato dei punti dove la funzione fa un salto" la convergenza della serie deve essere "arbitrariamente lenta". Indipendentemente da Seidel, ad analoghe conclusioni era giunto anche George G. Stokes (1819-1903), che parlava di convergenza "infinitamente lenta" della serie. Entrambe le formule saranno abbandonate in favore di quella di convergenza 'uniforme', che dal 1841 Weierstrass utilizzava

in un contesto e con motivazioni del tutto diverse. Dalle lezioni sulla teoria delle funzioni ellittiche che Christoph Gudermann (1798-1852) teneva a Münster, Weierstrass aveva appreso dell'esistenza di sviluppi in serie che avevano la proprietà di essere convergenti "in ugual grado" (o uniformemente, come si dice oggi) su un intervallo. Questo significava che per ogni numero ε>0 arbitrariamente piccolo si poteva trovare un numero n, dipendente da ε, tale che il resto della serie a partire dal termine n-esimo fosse, in valore assoluto, minore di ε, per ogni x appartenente all'intervallo. La richiesta della convergenza 'uniforme' metteva il teorema di Cauchy al riparo da ogni obiezione. Di questa nozione Weierstrass si servì sistematicamente in alcuni lavori sulle serie di potenze, rimasti inediti per oltre mezzo secolo, nei quali si trovano gli elementi essenziali della concezione 'aritmetica' del rigore in analisi, che egli presenterà nelle lezioni berlinesi a partire dal 1863-1864.

Di fatto, dopo oltre vent'anni, i matematici cominciavano a far luce nell'intricata matassa dei modi di convergenza di una serie di funzioni che si nascondevano dietro il teorema di Cauchy. D'altra parte, le ricerche inaugurate da Dirichlet avevano lasciato intravedere le delicate questioni di analisi legate al comportamento delle serie di Fourier, che richiedevano un deciso raffinamento di concetti e di metodi per essere affrontate con successo.

Tra Gottinga e Berlino

Nel 1854 Georg Friedrich Bernhard Riemann (1826-1866), che aveva seguito i corsi di Dirichlet a Berlino e si era laureato a Gottinga con una tesi sui fondamenti dell'analisi complessa sostenne la sua prova di abilitazione a Privatdozent (libero docente). Argomento dello scritto era la rappresentabilità delle funzioni in serie trigonometriche. Dopo una introduzione di carattere storico, largamente basata sui ricordi del periodo parigino con Dirichlet e delle conversazioni avute con Fourier, Riemann prendeva le mosse dalle conclusioni enunciate dallo stesso Dirichlet nel 1829. "In effetti, per tutti i casi che si presentano in natura la questione era completamente risolta", affermava Riemann. Particolarmente interessanti erano tuttavia i casi non discussi da Dirichlet, che erano intimamente legati ai concetti fondamentali del calcolo infinitesimale, a cominciare dal concetto di integrale. "Che cosa si deve intendere con ∫^b_af(x)dx?" si chiedeva Riemann. La risposta consisteva nella definizione di integrale che porta il suo nome, una generalizzazione di quella data a suo tempo da Cauchy. La condizione necessaria e sufficiente per stabilire se una funzione fosse o meno integrabile secondo la sua nuova definizione era che la funzione fosse limitata e "l'ampiezza totale dell'intervallo in cui le oscillazioni della funzione sono maggiori di σ, qualunque sia σ, possa essere resa arbitrariamente piccola". Naturalmente, funzioni integrabili secondo Cauchy erano ancora integrabili secondo Riemann e il valore dell'integrale era lo stesso. Tuttavia si trattava di un'effettiva estensione della definizione di Cauchy, come Riemann mostrava mediante l'esempio dell'integrale di una funzione discontinua in ogni punto razionale; non integrabile secondo Cauchy, ma integrabile secondo la nuova definizione. Quanto alla questione centrale del suo lavoro, la rappresentabilità delle funzioni in serie trigonometriche, Riemann rovesciava lo schema seguito fino ad allora. Invece di provare che se la funzione aveva proprietà opportune (da specificare, come aveva fatto Dirichlet), allora poteva essere rappresentata in serie di Fourier, Riemann si poneva la domanda inversa: se una funzione era rappresentabile in serie trigonometrica, quali erano le conseguenze sul suo comportamento? Come variava il valore della funzione al variare di x? Pur non riuscendo a trattare in tutta generalità i casi esclusi dalle condizioni di Dirichlet, Riemann arrivava tuttavia a dimostrare una condizione necessaria e sufficiente che, sotto opportune ipotesi, assicurava l'esistenza di una serie trigonometrica rappresentante la funzione data. Nella parte conclusiva del suo scritto Riemann forniva numerosi esempi di funzioni dal comportamento 'patologico', funzioni integrabili ma non rappresentabili in serie di Fourier e viceversa, serie trigonometriche che rappresentano funzioni non integrabili, e così via.

Sarà proprio lo studio di questi casi 'eccezionali' ad attirare l'attenzione dei matematici dopo il 1867, quando lo scritto di abilitazione di Riemann fu pubblicato postumo. Di analoghe funzioni 'patologiche' il matematico di Gottinga doveva aver discusso anche nei suoi corsi, se in una comunicazione all'Accademia delle Scienze di Berlino del 1872 Weierstrass affermava di aver saputo da uno studente che Riemann sosteneva a lezione che la funzione rappresentata dalla serie

contraddiceva il cosiddetto 'teorema di Ampère', secondo cui una funzione continua è sempre derivabile (tranne al più in punti isolati). Invece di tentare di darne una dimostrazione (solo nel 1970 è stato dimostrato che la funzione di Riemann ha derivata uguale a −1/2 in un'infinità di punti irrazionali), Weierstrass preferiva proporre un proprio esempio, che gli era stato suggerito dalle sue ricerche sulla possibilità di 'prolungare analiticamente' in ogni parte del piano una funzione di variabile complessa definita da una serie di potenze. Mettendo a frutto la nozione di convergenza uniforme di una serie di funzioni, egli dimostrava che la funzione

è continua ma non possiede in nessun punto derivata se a è intero dispari, 0⟨b⟨1 e ab>1+3π/2. Non era la prima volta che Weierstrass criticava pubblicamente affermazioni e risultati di Riemann. Né era un mistero che "a Berlino le cose del Riemann fecero difficoltà", come aveva annotato Felice Casorati (1835-1890) nel 1864 durante un soggiorno nella capitale prussiana. Quello che veniva messo in discussione dai matematici berlinesi, proprio dal punto di vista del rigore, era il ruolo attribuito da Riemann all'intuizione geometrica, il punto di vista geometrico da lui adottato nella teoria delle funzioni di variabile complessa, anche nei passi più delicati e decisivi. La stessa cosa era avvenuta con il suo uso del cosiddetto 'principio di Dirichlet' per stabilire teoremi fondamentali, quali il teorema di esistenza di una funzione di variabile complessa o il teorema di rappresentazione di Riemann. "Se una funzione cresce e poi diminuisce o viceversa ‒ diceva Leopold Kronecker (1823-1891) a Casorati ‒ Riemann dice dovervi essere un massimo o un minimo (vedi la dimostrazione del cosiddetto Dirichlet'sche Prinzip) mentre si dovrebbe restringere la conclusione alla sfera delle funzioni per così dire ragionevoli" (in Bottazzini 1986, p. 262). Qui Kronecker implicitamente alludeva alla distinzione tra estremo superiore (o inferiore) e massimo (rispettivamente minimo) che, stabilita da Bolzano e ben presto dimenticata, era stata indipendentemente riscoperta da Weierstrass e dai matematici berlinesi.

D'altra parte, proprio la considerazione di funzioni 'irragionevoli' aveva permesso a Riemann di estendere il concetto di integrale e consentiva in quegli anni di precisare rigorosamente concetti apparentemente consolidati come quello di continuità ‒ ancora "un'idea confusa" a parere di Kronecker ‒ così come il rapporto tra continuità e derivabilità di una funzione. Mediante un'analisi rigorosa dei teoremi di Cauchy e Abel sulle serie di funzioni continue, Kronecker aveva, per esempio, scoperto che "Abel, nella memoria sulla serie binomiale (dove non definisce abbastanza nettamente la continuità) correggendo l'errore di Cauchy, dà una dimostrazione che non vale". L'argomento di Abel si basava sull'esistenza di un massimo per una certa funzione limitata ma, osservava Kronecker, egli "non considerava che se quel limite superiore dipende dall'x, non si può asserire l'esistenza del massimo". Altrettanto cruciale era la distinzione tra "puntuale" e "uniforme" per la continuità delle funzioni e la convergenza delle serie o quella tra estremo superiore (inferiore) e massimo (minimo) di un insieme di numeri reali.

Critiche di questo tipo diventarono di pubblico dominio nel 1870, quando Weierstrass comunicò all'Accademia delle Scienze di Berlino una breve nota in cui, mettendo a frutto la distinzione tra estremo inferiore e minimo, mostrava come fossero 'assolutamente fondati' i dubbi che erano stati avanzati sull'ammissibilità del 'principio di Dirichlet'. Egli cominciava con il considerare una qualunque funzione continua e derivabile sull'intervallo [−1,1] tale che f(−1)=a, f(1)=b, e a≠b. Se il ragionamento di Dirichlet fosse ammissibile, continuava Weierstrass, allora tra tutte le funzioni che soddisfano le condizioni richieste se ne dovrebbe "trovare una particolare, per la quale il valore dell'integrale

è uguale all'estremo inferiore di tutti i valori che questo integrale può assumere per le diverse funzioni f(x) che appartengono all'insieme considerato" (Weierstrass, 1894-1927, I, p. 52). Si dimostra facilmente che quell'estremo è uguale a zero, e tuttavia, comunque si scelga la f(x) sotto le ipotesi date, non può essere raggiunto da J, perché in tal caso df(x)/dx=0, e dunque f(x)=costante, che contraddice la condizione a≠b. Il principio di Dirichlet portava "manifestamente a un risultato falso" concludeva Weierstrass, minando con ciò le basi dell'intera teoria riemanniana delle funzioni di variabile complessa.

Da quando era stato chiamato a insegnare a Berlino nel 1856, Weierstrass aveva rivolto la sua attenzione soprattutto alla creazione di una rigorosa teoria di quelle funzioni, le 'funzioni analitiche' nella terminologia che Weierstrass riprendeva da Lagrange, su cui costruire l'edificio delle funzioni ellittiche e abeliane, che erano al centro dei suoi interessi. Secondo Weierstrass, il raggiungimento di un rigore assoluto costituiva un obiettivo essenziale del programma che aveva delineato e andava svolgendo nei suoi corsi. A suo parere, il rigore auspicato si poteva ottenere abbandonando il terreno intuitivo dell'evidenza geometrica e ponendo invece l'aritmetica dei numeri naturali a fondamento dei concetti e delle strutture dell'analisi, come egli mostrava nei suoi corsi di introduzione agli elementi della teoria delle funzioni analitiche mediante la costruzione rigorosa del campo dei numeri reali e dei numeri complessi, preliminare per ogni ulteriore considerazione sulle funzioni.

Continuità e insiemi infiniti di punti

Il punto di vista di Weierstrass, inizialmente noto solo ai suoi studenti e colleghi dell'Università di Berlino, cominciò a diffondersi nella comunità dei matematici all'inizio degli anni Settanta. Eduard Heine (1821-1881), un allievo di Gauss divenuto professore a Halle, ne dava una presentazione sistematica nell'articolo Die Elemente der Funktionenlehre (1872). Nello stesso anno Richard Dedekind (1831-1916) e Georg Cantor (1845-1918) pubblicavano le loro teorie dei numeri reali, che si affiancavano a quella di Weierstrass nel dare una sistemazione rigorosa al concetto di continuità. Come Riemann, anche Dedekind era stato allievo di Gauss ed era stato profondamente influenzato da Dirichlet, che si era trasferito a Gottinga nel 1855 dopo la morte di Gauss. Tre anni più tardi Dedekind era stato chiamato a insegnare al Politecnico di Zurigo; a quel periodo risalivano le prime idee che egli presentava nell'opuscolo Stetigkeit und irrazionale Zahlen (Continuità e numeri irrazionali). Era stato proprio l'insegnamento a convincerlo infatti della necessità di trovare un fondamento "scientifico" al calcolo infinitesimale. Secondo Dedekind, la "vera origine" di quel calcolo andava ricercata negli elementi dell'aritmetica, che consentivano, al tempo stesso, "una definizione effettiva della continuità". Egli prendeva le mosse dal campo dei numeri razionali e dalla corrispondenza tra questi e i punti della retta. Tuttavia, come già sapevano gli antichi Greci, esistono grandezze come la diagonale e il lato di un quadrato che sono incommensurabili tra loro, e dunque segmenti che sono incommensurabili rispetto a una data unità di misura. "La retta è infinitamente più ricca di punti che non il campo razionale di numeri", affermava Dedekind, e i numeri razionali non consentono di descrivere aritmeticamente le sue proprietà. Si rendeva indispensabile l'ampliamento del campo dei razionali "creando nuovi numeri" per ottenere un campo numerico "altrettanto continuo come lo è la retta". Quale era, però, la proprietà caratteristica della continuità, la sua essenza come diceva Dedekind? La risposta era affidata a un assioma: se si ripartiscono tutti i punti della retta in due classi in modo che ogni punto di una delle due classi stia a sinistra di ogni punto dell'altra, allora esiste uno e un solo punto che produce tale ripartizione. Questo assioma indicava a Dedekind la via per giungere a una caratterizzazione aritmetica della continuità. Ogni numero razionale produceva infatti una 'sezione' (A₁, A₂) di quei numeri in due classi, tali che ogni numero in A₁ è minore di ogni numero in A₂ e inoltre o A₁ aveva un massimo o A₂ aveva un minimo. E viceversa, ciò caratterizzava le sezioni prodotte da numeri razionali. Non era difficile, però, accorgersi che esistevano infinite sezioni che non erano prodotte da alcun numero razionale. "Orbene ‒ concludeva Dedekind ‒ ogni volta che è data una sezione (A₁,A₂) che non sia prodotta da alcun numero razionale, noi creiamo un nuovo numero irrazionale α, che consideriamo completamente definito da questa sezione" (1872 [1926, p. 132]). Il nuovo campo numerico dei numeri reali, così ottenuto, soddisfaceva all'assioma della continuità, come Dedekind mostrava provando il teorema secondo cui, per una qualunque sezione (A₁,A₂) di numeri reali, esiste uno e un solo numero reale α, dal quale la sezione è prodotta.

Mentre ultimava la redazione del suo scritto Dedekind venne a conoscenza di un articolo di Cantor sulle serie trigonometriche, in cui si trovava formulato un assioma sostanzialmente equivalente al suo assioma di continuità. Cantor aveva studiato a Berlino dove aveva ottenuto l'abilitazione a Privatdozent con una tesi di teoria dei numeri sotto la guida di Kronecker. Chiamato poi a insegnare a Halle nel 1869, su suggerimento di Heine aveva cominciato a dedicarsi a ricerche sulle serie trigonometriche, che la pubblicazione dello scritto di Riemann aveva reso argomento di grande attualità. "Un capolavoro è la definizione di integrale definito" scriveva entusiasta Jean-Gaston Darboux (1842-1917) che nel lavoro di Riemann trovò fonte d'ispirazione per una grande memoria sulle singolarità e le discontinuità delle funzioni apparsa nel 1875. Anche Hermann Hankel (1839-1873) si era ispirato a Riemann nel suo studio di funzioni 'patologiche', come le funzioni 'discontinue e infinitamente oscillanti' oggetto di un suo lavoro pubblicato postumo nel 1882.

Il problema che Heine sottopose al suo giovane collega riguardava l''unicità' della rappresentazione di una funzione in serie trigonometrica. L'interesse di tale problema risiedeva nella tacita convinzione di ottenere sempre la stessa serie, qualunque fosse la strada seguita per sviluppare la funzione in serie trigonometrica. Nei loro lavori Dirichlet, Riemann, e successivamente Rudolf Otto Sigismund Lipschitz (1823-1903), avevano dimostrato che sotto ipotesi molto generali una funzione era rappresentabile in quel modo. Si erano tuttavia serviti di un procedimento di integrazione di una serie termine a termine che, come aveva mostrato Weierstrass, era legittima solo se la serie era uniformemente convergente e "a tutt'oggi ‒ scriveva Heine nel 1870 ‒ non si sa neppure se sia possibile rappresentare una funzione continua data, mediante una serie trigonometrica uniformemente convergente". La questione, che Heine lasciava aperta, riceverà una risposta negativa nel 1876 da parte di Du Bois-Reymond, mentre Heine riuscì a dimostrare che se una serie trigonometrica uniformemente convergente nell'intervallo [−π,π] vi rappresentava lo zero dappertutto tranne che in un numero finito di punti, allora si dovevano annullare tutti i suoi coefficienti e la serie rappresentava lo zero in ogni punto dell'intervallo. Da questo teorema prendeva le mosse Cantor, in quello stesso anno, per dimostrare che "una rappresentazione dello zero in serie trigonometrica convergente per ogni valore reale di x è possibile solo se i coefficienti della serie sono tutti uguali a zero", da cui discendeva il teorema di unicità cercato. Qualche tempo dopo Cantor indeboliva le ipotesi del suo teorema dimostrando che esso continuava a valere se per certi valori di x "viene meno o la rappresentazione dello zero mediante la serie oppure la convergenza" di quest'ultima. Questi punti 'eccezionali' potevano essere in numero finito oppure, come mostrava in un articolo del 1872, anche in numero infinito, purché distribuiti in maniera opportuna. Era questo l'articolo cui si riferiva Dedekind. Alla dimostrazione del suo teorema Cantor premetteva una teoria aritmetica dei numeri reali, che egli definiva per mezzo di successioni a₁,a₂,…,a_n,… di numeri razionali caratterizzate dalla proprietà che "per ogni valore razionale positivo ε esiste un intero n₁, tale che ∣a_n+m−a_n∣⟨ε per n>n₁ e per ogni m intero positivo". A ognuna di queste successioni 'fondamentali' (oggi dette 'di Cauchy') Cantor associava un numero b, definito a meno di una relazione di equivalenza per le successioni e il campo dei numeri reali era l'insieme di tali numeri.

Il procedimento si poteva reiterare, generando così numeri reali 'di tipo superiore' considerando successioni 'fondamentali' di numeri b i nuovi numeri c a esse associati e così via. Enti inutili, secondo Dedekind, dotati invece di significato preciso secondo Cantor. Gli oggetti ottenuti con questa costruzione puramente astratta si lasciavano infatti interpretare in termini di insiemi 'derivati' di punti, che Cantor definiva a partire dal concetto di punto-limite (o punto di accumulazione) di un insieme infinito di punti. Un punto-limite di un insieme P era "un punto della retta ‒ spiegava Cantor ‒ tale che in ogni suo intorno si trovino infiniti punti dell'insieme P, con il che può capitare che egli stesso non appartenga all'insieme". Egli dimostrava il cosiddetto teorema di Bolzano-Weierstrass (un insieme limitato e infinito di punti ha sempre almeno un punto di accumulazione) e considerava poi l'insieme P′ costituito dai punti di accumulazione di P e la successione P′,P″,… ottenuta reiterando il procedimento di 'derivazione', che a Cantor appariva concettualmente analogo alla costruzione di numeri reali 'di tipo superiore'. Cantor chiamava di 'prima specie' gli insiemi infiniti di punti per cui il processo di derivazione si arrestava dopo n passi, giungendo a un insieme costituito di un numero finito di punti, e nell'ultima parte del suo articolo mostrava che il teorema di unicità della rappresentazione in serie trigonometrica sussisteva se l'insieme dei punti eccezionali della funzione era di prima specie. Un grande e sorprendente risultato, che suscitò l'ammirazione dei matematici. A quell'epoca Cantor era però più interessato ai preliminari che alle conseguenze del suo teorema, e immaginava la possibilità di reiterare infinite volte il procedimento di derivazione, creando una "generazione dialettica di concetti che conduce sempre più lontano e, libera da ogni arbitrarietà, resta in sé necessaria e conseguente". Quando Cantor scriveva queste righe, all'inizio degli anni Ottanta, la teoria degli insiemi transfiniti, nel 1872 solo intravista, dominava ormai completamente i suoi interessi.

La necessità di caratterizzare in maniera più precisa l'infinità dei punti 'eccezionali' ammessa per il suo teorema portò Cantor e Dedekind, con il quale era entrato in corrispondenza, a classificare gli insiemi infiniti secondo la loro 'potenza' ‒ insiemi numerabili come i numeri razionali e i numeri algebrici, che si potevano mettere in corrispondenza biunivoca con l'insieme dei numeri naturali; insiemi più che numerabili, con la 'potenza del continuo' come l'insieme dei numeri reali. D'altra parte, i risultati di Cantor sugli insiemi infiniti di punti della retta si rivelavano di grande fecondità per l'analisi, come ben presto mostrò Ulisse Dini (1845-1918). Nei suoi volumi, Fondamenti per la teorica delle funzioni delle variabili reali (1878) e Serie di Fourier e altre rappresentazioni analitiche (1880), Dini rendeva noti i risultati della sua rigorosa e sofisticata analisi dell'argomento.

All'inizio degli anni Ottanta del XIX sec., con i lavori di Dedekind e Cantor, e il prevalere della 'scuola' di Weierstrass a Berlino, si stava ormai definitivamente affermando la tendenza all'aritmetizzazione dell'analisi, come la chiamò Christian Felix Klein (1849-1925) nel 1895. Il rigore logico era un elemento essenziale del pensiero matematico, affermava allora Klein, ma certo "la matematica non è per nulla esauribile con la deduzione logica". Rivendicando all'intuizione "la sua piena e specifica efficacia" Klein lasciava intravedere i termini del dibattito sui fondamenti, che doveva caratterizzare la matematica nei decenni a venire.

Bibliografia

Belhoste 1991: Belhoste, Bruno, Augustin-Louis Cauchy. A biography, translated by Frank Ragland, New York-Berlin, Springer, 1991 (ed. orig.: Cauchy 1789-1857. Un mathématicien légitimiste au XIXème siècle, Paris, Belin, 1988).

Bottazzini 1986: Bottazzini, Umberto, The higher calculus. A history of real and complex analysis from Euler to Weierstrass, translated by W. von Egmond, Berlin-New York, Springer, 1986 (ed. orig.: Il calcolo sublime. Storia dell'analisi matematica da Euler a Weierstrass, Torino, Boringhieri, 1981).

‒ 1990: Bottazzini, Umberto, 'Geometrical rigour' and 'modern analysis'. An introduction to Cauchy's 'Cours d'analyse', in: Cauchy, Augustin-Louis, Cours d'analyse de l'École Royale Polytechnique. Analyse algebrique, rist. facs. dell'ed. 1821, a cura di Umberto Bottazzini, Bologna, Clueb, 1990-1992, 2 v.; v. I, 1990, pp. XI-CLXVII.

‒ 2001: Changing images in mathematics. From the French Revolution to the new millennium, edited by Umberto Bottazzini and Amy Dahan-Dalmédico, London, Routledge, 2001.

Dahan-Dalmédico 1992: Dahan-Dalmédico, Amy, Mathématisations. Augustin-Louis Cauchy et l'École française, Paris, Blanchard, 1992.

Dauben 1979: Dauben, Joseph Warren, Georg Cantor: his mathematics and philosophy of the infinite, Cambridge (Mass.), Harvard University Press, 1979 (2. ed.: Princeton, Princeton University Press, 1990).

Dhombres 1998: Dhombres, Jean - Robert, Jean-Bernard, Joseph Fourier (1768-1830), créateur de la physique-mathématique, Paris, Belin, 1998.

Dugac 1973: Dugac, Pierre, Éléments d'analyse de Karl Weierstrass, "Archive for history of exact sciences", 10, 1973, pp. 41-176.

‒ 1976: Dugac, Pierre, Richard Dedekind et les fondements des mathématiques, Paris, Vrin, 1976.

Gilain 1989: Gilain, Christian, Cauchy et le cours d'analyse de l'École Polytechnique, "Bulletin de la Société des Amis de la Bibliothèque de l'École Polytechnique", 5, 1989, pp. 3-145.

Grabiner 1981: Grabiner, Judith V., The origins of Cauchy's rigorous calculus, Cambridge (Mass.)-London, MIT Press, 1981.

Grattan-Guinness 1972: Grattan-Guinness, Ivor - Ravetz, Jerome R., Joseph Fourier 1768-1830, a survey of his life and work, based on a critical edition of his monograph on the propagation of heat, presented to the Institut de France in 1807, Cambridge (Mass.), MIT Press, 1972.

‒ 1990: Grattan-Guinness, Ivor, Convolutions in French mathematics, 1800-1840, Basel, Birkhäuser, 1990, 3 v.

Jahnke 1999: Geschichte der Analysis, hrsg. von Hans Niels Jahnke, Heidelberg-Berlin, Spektrum Akademischer Verlag, 1999.

Laugwitz 1996: Laugwitz, Detlef, Bernhard Riemann, 1826-1866. Wendepunkte in der Auffassung der Mathematik, Basel, Birkhäuser, 1996.

Smithies 1986: Smithies, Frank, Cauchy's conception of rigour in analysis, "Archive for history of exact sciences", 36, 1986, pp. 41-62.

Stubhaug 2000: Stubhaug, Arild, Niels Henrik Abel and his times, translated by Richard H. Daly, Berlin-London, Springer, 2000.