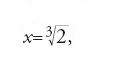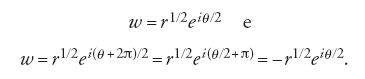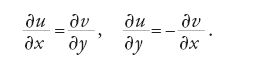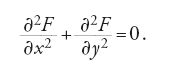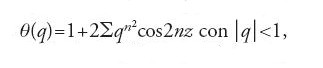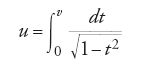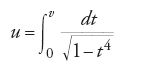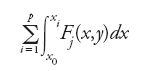L'Ottocento: matematica. Analisi complessa

di Jeremy Gray - Storia della Scienza (2003)

Jeremy Gray

Analisi complessa

Lo sviluppo dell'analisi complessa è una delle caratteristiche salienti della matematica del XIX secolo. Lo studio di funzioni complesse di una variabile complessa era stato affrontato sporadicamente nel corso del secolo precedente e i numeri complessi erano stati introdotti nello studio delle funzioni trigonometriche, nell'integrazione delle funzioni razionali, nella risoluzione di equazioni polinomiali, nella teoria dei numeri (in relazione all'ultimo teorema di Fermat), nello studio delle applicazioni conformi e nella cartografia teorica. Molto spesso, però, il loro uso aveva un carattere più formale che sostanziale, in accordo con l'orientamento in materia di algebra predominante nel XVIII secolo. Nel XIX sec. fu invece elaborata una ricca teoria delle funzioni di variabili complesse e l'analisi complessa acquisì una dignità pari a quella dell'analisi reale. Ciò fu dovuto sia alla possibilità di passare dal dominio reale a quello complesso in modo agevole e matematicamente naturale, sia agli aspetti particolarmente proficui di tale passaggio (riguardanti, per es., lo studio delle equazioni polinomiali dal punto di vista geometrico e l'intimo legame con le funzioni armoniche).

Il cammino tortuoso che ha portato alla definizione dei numeri complessi percorre un arco di tempo che va dal XVI alla metà del XIX sec., ma lo studio delle funzioni complesse si è svolto per molti aspetti in maniera indipendente in quanto, secondo la maggior parte dei matematici, i problemi con i numeri complessi emergevano dal loro impiego nella teoria delle funzioni, non in algebra. Jean Baptiste Le Rond d'Alembert (1717-1783) e Leonhard Euler (1707-1783), per esempio, discussero a lungo sul significato da attribuire al logaritmo di un numero complesso. D'Alembert pensava che ogni numero complesso dovesse avere un unico logaritmo; Euler aveva invece assunto la posizione ‒ che alla fine sarebbe prevalsa ‒ secondo la quale il logaritmo di un numero complesso dovesse avere infiniti valori. Ancora nel 1843, Carl Friedrich Gauss (1777-1855) insisteva sulla differenza fra definizione dei numeri complessi e loro rappresentazione come punti del piano, tuttavia questa sottile distinzione non gli impedì di elaborare una teoria delle funzioni di variabile complessa fondata su considerazioni geometriche. In verità l'annullamento di tale distinzione, senza eccessive preoccupazioni per le sue implicazioni filosofiche, fu la strada seguita da molti matematici; mentre Gauss, come risulta dalla corrispondenza del 1811 con l'astronomo Friedrich Wilhelm Bessel (1784-1846), richiedeva a chiunque intendesse introdurre una nuova funzione in analisi, di spiegare

se intende calcolarla solo per quantità reali, considerando i valori immaginari dell'argomento come elementi, per così dire, secondari, o se è d'accordo con il mio principio che gli immaginari debbano godere degli stessi diritti dei reali nel dominio delle quantità. Non si tratta di una questione di utilità pratica: secondo me, l'analisi è una scienza indipendente che perde molto in bellezza e armonia se si trascura qualsiasi quantità fittizia; e in un momento tutte le verità, che altrimenti varrebbero in generale, devono essere necessariamente gravate dalle più pesanti restrizioni. (Gauss 1863-1933, X, 1, p. 366)

Il fatto che Gauss potesse includere in una sua affermazione sia 'quantità fittizie' sia 'verità generali' costituisce un sorprendente indizio della tensione esistente tra matematica e filosofia della matematica. Occorre spiegare in quale modo quantità fittizie possano condurre a verità generali. Innanzi tutto, come indicazione delle verità che aveva in mente, Gauss proseguiva la sua lettera a Bessel con una riflessione sugli integrali nel campo complesso. Dopo aver osservato che il valore di un tale integrale può dipendere talvolta dal cammino che congiunge estremi di integrazione, scriveva:

L'integrale ∫φ(x)dx lungo due diversi cammini ha sempre lo stesso valore se non accade mai che φ(x)=∞ nella regione compresa tra le curve che costituiscono i cammini. Questo è un bellissimo teorema di cui intendo fornire dimostrazione, non troppo difficile, al momento opportuno. […] In ogni caso, questo fatto chiarisce immediatamente perché una funzione definita a partire da un integrale ∫φ(x)dx possa assumere più valori in corrispondenza di un singolo valore di x: è possibile girare attorno a un punto in cui φ(x)=∞ una, nessuna, o più volte. Per esempio, definendo logx come ∫dx/x e partendo da x=1, si può arrivare a logx senza girare intorno al punto x=0, oppure girandoci intorno una sola volta o girandoci intorno più volte; ogni volta bisogna sommare la costante 2πi o −2πi. Risulta pertanto chiaro perché un numero complesso abbia molti logaritmi. (ibidem)

In questo caso la verità non riguarda tanto il fatto che il logaritmo sia una funzione a più valori di una variabile complessa, quanto la ragione di tale fenomeno, da ricercarsi negli aspetti geometrici del problema. La rappresentazione delle quantità fittizie è all'origine della verità e Gauss era sempre attento a porre in rilievo l'importanza di trovare congrue ragioni soggiacenti. Si è già accennato alla natura fittizia dei numeri complessi, ma si deve di nuovo osservare l'inadeguatezza della filosofia, o meglio notare che il contrasto tra la nuova teoria delle funzioni di variabili complesse e la vecchia filosofia della matematica, adeguata per la geometria classica e per l'aritmetica, non era più conciliabile. Come in molti altri dibattiti filosofici, non ci fu mai un confronto decisivo: lo stile di tali dibattiti non è quello della pubblica abiura. Vi fu invece un nuovo orientamento, segnato nel modo più evidente dai lavori di Georg Friedrich Bernhard Riemann (1826-1866) e del suo precursore, il filosofo Johann Friedrich Herbart (1776-1841), verso la semplice accettazione delle grandezze bidimensionali, e più in generale n-dimensionali, come grandezze fondamentali. A favorire questo cambiamento non furono solo i numeri complessi: nella prima metà del XIX sec. vi contribuì anche la 'preistoria' del calcolo vettoriale.

Restano due osservazioni conclusive. La filosofia algebrica formale della matematica non sparì completamente: resta infatti viva ancor oggi in varie forme. Per quanto riguarda la storia della teoria delle funzioni di variabili complesse, l'interessante distinzione pratica che occorre tener presente riguarda la teoria algebrica e la teoria geometrica di tali funzioni. Infine, ci si può domandare perché la comprensione della natura di √−1 fosse diventata un problema così urgente negli anni immediatamente successivi al 1800.

La quasi totale assenza dal dibattito dei matematici più importanti dell'epoca induce a pensare che l'attenzione sui fondamenti teorici non sia scaturita dalle ricerche più avanzate sull'argomento e che, verosimilmente, la lenta crescita di interesse per i numeri complessi durante il XVIII sec. abbia semplicemente reso attuale il problema. La singolare prevalenza di nomi francesi, però, suggerisce un'altra ipotesi. Sull'onda dei grandi sconvolgimenti seguiti alla Rivoluzione francese, può darsi che molti vecchi luoghi comuni siano stati finalmente ritenuti criticabili. Ipotesi, questa, che sembra non sussistere, dato che si deve ammettere che matematici innovativi abbiano sostenuto posizioni politiche reazionarie, come fece Cauchy per tutto il corso della sua vita. Anche non volendo attribuire una causa così importante a un dibattito tanto oscuro, si può ancora notare che a partire dal 1795 il nuovo governo francese assegnò alla matematica un rango elevato e produsse un gran numero di matematici con una preparazione di alto livello, ai quali furono riservati impieghi nel campo dell'istruzione superiore e tra il personale più qualificato del Genio civile e militare; furono inoltre fondate nuove riviste per pubblicare le loro idee e non è molto sorprendente che alcuni, constatando che dopo tutto la filosofia dei numeri complessi non era stata adeguatamente compresa, abbiano voluto offrire le loro spiegazioni.

Il teorema fondamentale dell'algebra

Il teorema fondamentale dell'algebra afferma che ogni equazione algebrica a coefficienti reali o complessi ha almeno una radice complessa (Tav. Ia e Ib).

Ne deriva che ogni equazione algebrica di grado n ha esattamente n radici (non necessariamente distinte). Tralasciando le sue applicazioni all'algebra, durante il XVIII sec. ne era stata riconosciuta l'utilità per il calcolo degli integrali. Precisamente, per integrare una funzione razionale della forma p(x)/q(x) è sufficiente scomporre il denominatore q(x) nel prodotto di fattori (lineari e non lineari, l'esistenza dei quali è conseguenza diretta del teorema fondamentale dell'algebra), e poi utilizzare il metodo dei 'fratti semplici' per esprimere la funzione come somma di termini agevolmente integrabili. In definitiva, fattorizzato il denominatore, il processo di integrazione di una funzione razionale non presenta alcuna difficoltà.

La dimostrazione del teorema per un polinomio di grado dispari, a coefficienti reali, si basa su una proprietà dei numeri reali. Dopo aver ridotto, senza perdere di generalità, il polinomio alla forma xⁿ+a₁xⁿ⁻¹+…+a_n, osserviamo che il valore del polinomio è grande e negativo quando x è grande e negativa; è invece grande e positivo quando x è grande e positiva. Essendo il suo grafico continuo, esso deve intersecare l'asse delle ascisse almeno una volta. In un punto dove il grafico interseca l'asse delle ascisse il polinomio si annulla, e questo dimostra l'asserto. Il polinomio x³−2, che non ha zeri razionali e il cui grafico interseca l'asse delle ascisse nel punto in cui

è un semplice esempio che chiarisce alcuni aspetti importanti del teorema fondamentale dell'algebra; esso riguarda la natura dei numeri reali e della nozione di continuità, ma non ha nulla a che fare con l'algebra stessa. Molti matematici iniziarono ad accorgersene durante il XIX sec., e il primo di questi fu presumibilmente Bernhard Bolzano (1781-1848). Una conferma della natura analitica del problema è data dalla circostanza che ancora oggi una dimostrazione del fatto che il grafico di una funzione continua, negativa in un punto del suo insieme di definizione e positiva in un altro, debba necessariamente attraversare l'asse delle ascisse non risulta, per i polinomi, più semplice di quanto non sia nel caso generale.

La prima delle quattro dimostrazioni di Gauss del teorema fondamentale dell'algebra è uno dei documenti più importanti della matematica del XIX secolo. In essa Gauss avanza pesanti critiche nei confronti dei precedenti tentativi, operati, tra gli altri, da d'Alembert; ma anche questa sua prima dimostrazione si basa su assunzioni (non provate) riguardanti la natura delle curve algebriche. Gauss osserva che ci sono quattro possibilità per le radici di un'equazione algebrica: possono non esistere; possono esistere, ma non obbedire alle usuali regole dell'aritmetica; possono obbedire alle usuali regole dell'aritmetica, ma non essere numeri complessi; possono, infine, essere numeri complessi. Egli riteneva che la maggior parte delle dimostrazioni dell'epoca provava solo che la terza possibilità non può presentarsi: se le radici obbediscono alle usuali regole dell'aritmetica allora, necessariamente, sono numeri complessi. Questa conclusione lasciava irrisolto il problema dell'esistenza delle radici di un polinomio (e del fatto che le stesse obbediscano o meno alle leggi dell'aritmetica).

In effetti, il problema dell'esistenza delle radici venne riaperto intorno al 1800 e la natura dei numeri complessi divenne oggetto di molti approfondimenti. Si può pensare che la definizione di numero complesso sia stata definitivamente chiarita, se non da Rafael Bombelli nel XVI sec., almeno nel corso dei due secoli successivi. D'altra parte, è all'inizio del XIX sec. che il dibattito sui numeri complessi si fa più acceso. Si potrebbe supporre che tale dibattito sia scaturito dalle menti più acute e abbia impegnato i più grandi matematici dell'epoca. Tale supposizione non è affatto corretta, e non è difficile rendersi conto del motivo.

I matematici del XVIII sec. consideravano generalmente il simbolo √−1 come un simbolo formale, il cui unico scopo sarebbe quello di separare i due termini di una somma del tipo x+y√−1, e che obbedisce a regole ovvie, tra le quali: (√−1)²=−1. Questa teoria formale è molto simile a quella moderna, e offre una base sufficiente per sviluppare l'intera teoria delle funzioni di variabile complessa. Tuttavia, essa differisce dalla teoria moderna per quanto riguarda le assunzioni filosofiche su cui si basa, e questo è il punto fondamentale da tenere presente se si vuole cogliere il significato e l'importanza dei dibattiti del XIX sec.: ogni questione sulla natura di √−1 è da considerarsi strettamente filosofica.

In ogni periodo storico, matematica e filosofia della matematica dominante convivono in uno stato di perenne tensione. Sono pochi coloro che hanno competenze specifiche in entrambe le materie, e la matematica si sviluppa secondo linee che i filosofi possono non condividere. Un matematico, impegnato per esempio a scrivere una prefazione a un libro o a stimolare l'interesse di qualche studente, può delineare una filosofia della matematica che non regge a un'analisi critica, alla luce della sua stessa pratica. Viceversa, un filosofo può sostenere una posizione secondo la quale la matematica esistente, quella 'fatta dai matematici', non è valida. Questo è quanto è accaduto nel dibattito sui numeri complessi.

Vale la pena di osservare che lo stesso può dirsi dei numeri negativi. Nonostante la loro introduzione fosse accompagnata da alcune perplessità, come indica il nome che fu loro attribuito (numeri ficti), essi vennero rapidamente accettati in algebra. Da quel momento in poi i matematici, e anche i mercanti e i contabili, non incontrarono alcuna difficoltà con i numeri negativi anche se vi furono alcuni problemi relativi all'introduzione delle coordinate geometriche. Tuttavia, filosoficamente non potevano trovar posto in un sistema di grandezze geometriche e di numeri pensati per contare. Due pecore in un campo hanno attributi determinati (possono essere bagnate, arruffate, scalpitanti) ma la pecora che io devo a te, la 'pecora negativa' che io posseggo, non ha alcun attributo: il negativo di uno non è un numero per contare. Perfino un matematico del calibro di d'Alembert ripudiò i numeri negativi nel suo articolo per l'Encyclopédie sulla base di considerazioni analoghe, proponendo di pensarli come quantità positive, ma in un certo senso opposte. Alcuni filosofi della matematica inglesi, di una generazione successiva, tra i quali Frend, insistevano ancora su tale argomento, sostenendo che i numeri negativi non esistono, e che utilizzarli è una sciocchezza. George Peacock nel suo Treatise on algebra (1830) espose in modo contorto l'idea secondo la quale parlare di numeri negativi è un modo improprio di parlare di numeri positivi.

Il dibattito è istruttivo, anche se le posizioni di Frend sembrano eccessive. Una filosofia dei numeri, che li consideri come attributi di grandezze discrete o continue, non è in grado di dar conto dei numeri negativi; essi vanno considerati come costruzioni del pensiero ma non, a loro volta, come grandezze. Nonostante la palude filosofica in cui si erano apparentemente impantanati, i matematici procedevano bene, ma il problema doveva essere affrontato da chiunque ritenesse che la matematica fosse vera, in quanto sistema di deduzioni logiche (che preservano la verità) costruite a partire da affermazioni su oggetti percepiti con sufficiente chiarezza, come i numeri. Si può osservare anche che, ragionevolmente, ogni partito in tale dibattito prestava fede a ciò che conosceva meglio, anche quando partiti diversi erano riuniti nella stessa persona.

Accadde lo stesso con i numeri complessi e con il problematico numero √−1. Vari autori (Caspar Wessel in Danimarca, Carnot, l'abate Adrien-Quentin Buée e Jacques-Frédéric Français in Francia) suggerirono che il concetto appropriato fosse quello di segmento orientato nel piano. Secondo loro, il segno −1 denota un segmento di lunghezza 1 orientato da destra a sinistra e √−1 un segmento di lunghezza 1 diretto verso l'alto. Nell'Essai sur une manière de représenter les quantités imaginaires dans les constructions géométriques del 1806, Jean-Robert Argand aveva assunto una posizione più sottile, argomentando che √−1 si potrebbe ottenere ruotando il segmento unitario di un angolo retto in direzione antioraria. Questi punti di vista costituirono l'argomento di un dibattito sviluppato nelle pagine delle Annales di Joseph-Diez Gergonne nel 1813-1814: Gergonne, matematico a sua volta, sosteneva che non basta adornare con aggettivi il concetto di grandezza, e che tali tentativi sono incoerenti.

Questi dibattiti procedevano senza il contributo dei matematici più importanti (a parte d'Alembert), a meno che non si tenga conto di un'influenza indiretta quale fu quella di Adrien-Marie Legendre su Français. Bisogna svolgere indagini specifiche per comprendere cosa essi pensassero, e spesso non si scopre nulla. Il caso più eclatante, per l'impegno profuso allo scopo di definire la teoria delle funzioni di una variabile complessa, è quello di Cauchy. Per quasi tutta la vita egli condivise la vecchia interpretazione formale dei numeri complessi. Talvolta esponeva la teoria di Buée, ma professava di ignorare quella di Argand. Soltanto nel 1847 egli tentò di chiarire, per sua personale soddisfazione, l'argomento. Questa è una chiara prova del fatto che il dibattito sui fondamenti della matematica e i problemi di ricerca nella teoria delle funzioni fossero argomenti ben distinti.

L'altro caso da considerare è quello di Gauss, ed è il più istruttivo. Fin dalle Disquisitiones arithmeticae (1801), egli aveva illustrato i risultati cui era pervenuto nella teoria dei numeri con la rappresentazione dei numeri complessi come punti del piano. Per esempio, nella sua teoria sulla costruibilità con riga e compasso del poligono regolare di 17 lati, aveva scritto esplicitamente le coordinate dei 17 vertici in questa forma. Nel 1805, mentre studiava dal punto di vista della teoria dei numeri le equazioni algebriche di terzo e quarto grado, Gauss scriveva che "quei teoremi raggiungono la loro vera semplicità e naturale bellezza quando il campo dell'aritmetica viene ampliato in modo da comprendere gli interi immaginari". Quando, molto più tardi (nel 1832), pubblicò i suoi risultati, egli fu costretto a esporre la propria teoria dei numeri complessi secondo la vecchia concezione algebrica che essi fossero simboli della forma a+ib, rappresentabili come punti del piano.

Mentre l'utilità dei numeri complessi continuava a crescere, i matematici oscillavano tra la loro rappresentazione geometrica e la loro descrizione come coppie ordinate di numeri reali. Come succede quasi sempre con le dispute filosofiche, essi dimenticavano il ruolo centrale delle grandezze nella definizione di ciò di cui si occupa la matematica. In effetti, a partire dal 1843, con la pubblicazione dei quaternioni di William R. Hamilton (il risultato di non pochi anni di lavoro suo e di molti altri matematici) cominciarono a fiorire numerose proposte di nuove 'algebre': i quaternioni di Amatus Lusitanus (Juan Manuel) Rodrigues, e così via fino a George W. Peirce e oltre.

Origini della teoria delle funzioni complesse

Il primo lavoro di Augustin-Louis Cauchy (1789-1857) sull'analisi complessa è una memoria, presentata all'Institut de France nel 1814, sul calcolo di integrali reali impropri, con uno o entrambi gli estremi di integrazione infiniti. Tali integrali erano stati considerati da Euler, Pierre-Simon de Laplace (1749-1827) e Siméon-Denis Poisson (1781-1840) e, negli Exercises de calcul intégral (1811), da Adrien-Marie Legendre (1752-1833). Cauchy osservò che in molti casi gli integrali venivano calcolati "per mezzo di una sorta di induzione" basata sul "passaggio dal reale all'immaginario"; pensando, come Laplace, che a questo metodo mancasse una dimostrazione rigorosa, si impegnò nel tentativo di fornirne una, compiendo un'analisi formale delle funzioni di due variabili reali, e in particolare di quelle che soddisfano le equazioni oggi dette di Cauchy-Riemann (espresse da Cauchy in una oscura forma generalizzata). In quel periodo l'uso delle equazioni di Cauchy-Riemann in tale contesto era piuttosto frequente, anche se né Cauchy, né altri si rendevano conto della loro fondamentale importanza. Il modo in cui una funzione reale può essere estesa a una funzione complessa emerse più per caso che per un disegno preciso, e questa può essere la ragione per cui Legendre e Poisson, nella loro relazione sulla memoria, ritennero che la spiegazione di Cauchy e le illustrazioni del suo metodo non contenessero nulla di nuovo.

Legendre giudicò invece più originale la seconda parte della memoria, laddove Cauchy discute la possibilità di invertire l'ordine di integrazione in un integrale doppio. Cauchy focalizza l'attenzione sui punti singolari della funzione integranda, dove la stessa diventa infinita o indeterminata, mostrando come in certi casi si ottengano due valori distinti e ben determinati, a seconda dell'ordine di integrazione. Questi risultati sono alla base di due fra le più importanti teorie di Cauchy: la teoria degli integrali singolari (gli integrali reali per i quali la funzione integranda diventa infinita) e quella dei poli e dei residui delle funzioni analitiche.

Cauchy cominciò a insegnare all'École Polytechnique nel novembre del 1815; nel 1816 fu nominato professore di ruolo, e continuò a ricoprire tale carica presso quell'istituto fino al 1830. Egli era pertanto tenuto a scrivere libri di testo per i suoi studenti, e nel 1821 pubblicò il Cours d'analyse sull'analisi algebrica, seguito due anni dopo dal Résumé sul calcolo differenziale e integrale. I capitoli dal VII al XII del Cours contengono quella che Cauchy chiama "una nuova teoria degli immaginari". Nel capitolo X egli fornisce una dimostrazione del teorema fondamentale dell'algebra, già presentata in un articolo precedente, che afferma di aver derivato da un lavoro di Legendre (1808).

Come era piuttosto comune in quel periodo, Cauchy definisce i numeri immaginari quali "espressioni simboliche" della forma a+b√−1, dove a e b sono quantità reali (1821a, pp. 173-176), ma definisce i concetti matematici e le operazioni per queste espressioni in modo molto più preciso dei suoi predecessori. Una delle ragioni per cui la sua trattazione è così ampia, un totale di 55 pagine, va ricercata nella sua sensibilità nei confronti dei problemi posti dalla non univocità delle potenze razionali dei numeri immaginari, argomento che per profondità andava ben oltre le idee dei suoi contemporanei. Un problema molto dibattuto riguardava (2cosx)^m, con m razionale. Joseph-Louis Lagrange (1736-1813) aveva proposto un metodo per sviluppare questa funzione in serie di potenze, che sembrava produrre un solo valore, ma la sua opinione troppo ottimista era stata contraddetta da Poisson, che era stato suo studente, considerando il caso m=1/3 e x=π. Da 2^mcos^mx si ottiene 2^1/3(−1)^1/3 e quindi, mediante le formule di Abraham de Moivre, tre valori complessi distinti: 2^1/3(1+i√3)/2, 2^1/3(1−i√3)/2, e −2^1/3. Una diversa analisi forniva ancora un altro valore: 2^1/3/2, media aritmetica dei primi due.

Pur avendo identificato in modo convincente gli errori di Lagrange, Poisson non era stato capace di correggerli, e con il passare del tempo un numero sempre maggiore di matematici si era trovato ad affrontare problemi simili. Senza dubbio Cauchy aveva ben presente questa situazione quando cominciò a scrivere il Cours. Egli considera abbastanza semplice definire le funzioni razionali di una variabile immaginaria e dare significato a x^a (con a numero razionale), ma ritiene del tutto inadeguati i metodi convenzionali quando si debbano definire le funzioni logaritmiche e trigonometriche di una variabile complessa, per le quali propone di utilizzare le serie di potenze. In tale prospettiva egli definisce anzitutto le serie di potenze di una variabile reale a coefficienti complessi, per poi estendere la teoria al caso di una variabile complessa. Dimostra la convergenza della serie geometrica a termini immaginari

per valori reali di z tali che ∣z∣⟨1; quindi afferma, sulla base di un teorema che successivamente si dimostrerà dover essere soggetto a restrizioni, che la somma di questa serie è una funzione continua di z in quell'intervallo. Mostra poi come estendere la teoria a valori complessi di z, e infine definisce a^z, senz e cosz per valori immaginari di z.

Attraverso questo procedimento complicato, ma rigoroso, Cauchy definisce le funzioni algebriche e trascendenti elementari di una variabile complessa. Tuttavia non dice nulla sulla possibilità di fornire una definizione generale di funzione complessa di una variabile immaginaria. Questa doveva rimanere per circa venti anni una difficoltà mai sufficientemente chiarita nella sua ricerca matematica.

Negli anni immediatamente successivi, Cauchy intraprese molti studi sull'integrazione, che culminarono nel suo capolavoro del 1825, Mémoire sur les intégrales définies prises entre des limites imaginaires, sugli integrali in un dominio complesso, stranamente pubblicato solo come opuscolo e non in una rivista. In esso, riferendosi al Mémoire del 1814 (non ancora pubblicato) e ad altri suoi articoli, precisa la sua definizione degli integrali del tipo

dove x₀ e X sono limiti reali, ma f(x) può essere una funzione a valori reali o immaginari della variabile x. In un altro dei momenti di incoerenza che dovevano rendere il lavoro di Cauchy su questi argomenti così difficile da capire per i contemporanei, egli estende questa definizione al caso complesso per semplice analogia, senza preoccuparsi di cosa significhi per f essere funzione di una variabile complessa.

Cauchy fornisce però una definizione precisa dell'integrale risultante come integrale di linea e quindi, supposta la f(x+y√−1) continua e limitata in un rettangolo, dimostra con il calcolo delle variazioni che il valore del suo integrale è indipendente dal cammino di integrazione. Più precisamente, dimostra che nelle suddette ipotesi una variazione infinitesima del cammino non cambia il valore dell'integrale. È la prima volta che compare il teorema integrale di Cauchy. Vale la pena di osservare come in questo lavoro Cauchy parli di funzioni continue di una variabile 'immaginaria', un concetto che non aveva mai definito esplicitamente nei suoi lavori precedenti. Guardando al modo in cui faceva uso di tali funzioni, sembrerebbe che egli assumesse che fossero a un solo valore, prive di poli e, ipotesi fondamentale, con derivata continua. Altrove Cauchy considerò come ovvio il fatto che tali funzioni soddisfacessero le equazioni di Cauchy-Riemann. Tutte queste tacite assunzioni dovettero essere individuata ed esplicitate da autori successivi. Bisogna aggiungere, per sottolineare le possibilità di confusione, che ‒ ancora nel 1825 ‒ non era chiaro se Cauchy stesse lavorando con funzioni complesse piuttosto che con particolari coppie di funzioni reali.

D'altra parte, Cauchy continuò a produrre una grande quantità di risultati essenziali per lo sviluppo successivo della teoria delle funzioni di variabile complessa. Egli dimostrò la sua formula integrale per le funzioni con poli di ordine finito e la applicò al calcolo degli integrali reali (impropri). Successivamente, nel 1825, cominciò a pubblicare gli Exercices de mathématiques, il modo migliore per diffondere i risultati delle sue ricerche. A partire dal primo volume estese sistematicamente i metodi che aveva introdotto nel Mémoire sur les integrales e senza dare alcuna spiegazione li chiamò 'calcolo dei residui' (nome che rimase), introducendo un simbolo speciale per l'estrazione del residuo di una funzione. Verso la fine della sua esistenza dedicò qualche lavoro alle applicazioni di tali metodi e pubblicò alcuni raffinamenti della teoria dei residui, nei quali considerava il caso di un dominio circolare e di un anello. In questo modo stabilì l'importanza del nuovo calcolo, senza però fornirne una giustificazione trasparente.

La diffusione delle idee di Cauchy non fu facilitata dal suo estremismo politico, che lo condusse ad autoesiliarsi dal 1830 al 1838 in seguito alla caduta della monarchia borbonica. In quel periodo, nonostante alcune visite occasionali a Parigi, perse l'impiego all'École Polytechnique e con questo l'incentivo a presentare la teoria delle funzioni di variabile complessa con un dettaglio almeno paragonabile a quello adottato nella presentazione della teoria delle funzioni di variabili reali. Inoltre, e per ragioni che molti hanno trovato difficili da comprendere, Cauchy non sembra aver mai utilizzato, né mai citato per decenni il suo lavoro del 1825 e il suo teorema integrale. Freudenthal (1991) si chiese se Cauchy non l'avesse semplicemente dimenticato, limitandosi a considerare soltanto cammini rettangolari, circolari o sul bordo di un anello, e riferendosi al Mémoire ormai datato del 1814, invece che a quello del 1825. Non lo menzionò neppure in un lavoro presentato all'Académie il 3 agosto 1846, che è comunemente considerato lo scritto in cui apparve la prima formulazione generale del teorema integrale. Il paradosso però si ridimensiona leggendo quel lavoro, poiché in esso Cauchy non si riferisce mai alle funzioni complesse né all'integrazione complessa, ma allude invece al teorema di Green.

Tuttavia, sembra che la preparazione del lavoro abbia risvegliato molte idee che riposavano nella fertile mente di Cauchy. Una settimana dopo egli scrisse una nota in cui osservava per la prima volta che i principî enunciati nel suo Cours erano applicabili con considerevole generalità. Come osserva Morris Kline: "Cauchy deve aver pensato a lungo e intensamente per rendersi conto che alcune relazioni tra coppie di funzioni reali acquisiscono forma più semplice quando si introducono le quantità complesse" (Kline 1972, p. 638). In una serie di articoli, scritti con cadenza quasi settimanale, egli elaborò questo nuovo punto di vista. L'interpretazione geometrica di x+y√−1 fu introdotta per la prima volta, e di qui l'idea di integrale curvilineo lungo un cammino nel piano complesso. L'utilità del calcolo dei residui allontanò Cauchy dal problema delle funzioni a più valori, e fu solo per commentare la memoria di Victor Puiseux (1820-1883) del 1850 che tornò a considerare l'argomento. Sebbene fosse stato un problema relativo alla natura a più valori delle espressioni complesse a ispirare a Cauchy alcune delle sue prime intuizioni sulle funzioni di variabile complessa, egli non dominò mai completamente questo aspetto della teoria. In un lavoro sugli integrali ellittici del 1846 si avvicinò all'idea che i loro valori formassero una superficie connessa, ma dopo averla abbandonata, considerò la possibilità di dividere il dominio in parti, all'interno delle quali la funzione è a un solo valore, e di studiare il comportamento della funzione a più valori considerando i salti compiuti dalla funzione nell'attraversare i tagli. Nel frattempo, nel 1847, Cauchy cercò di definire ‒ quasi per soddisfare il suo interesse ‒ che cosa fosse un numero complesso, se non lo si voleva considerare un semplice artificio formale per fondere insieme due numeri reali. Suggerì diverse teorie. Una, ispirata ai lavori di Gauss e di Ernst Eduard Kummer (1810-1893) sulle classi di forme quadratiche, considerava equivalenti due polinomi reali nella variabile i che danno lo stesso resto nella divisione per i²+1, e definiva un numero complesso come una classe di equivalenza di polinomi. Nel 1849 Cauchy cambiò idea e ritornò alla teoria geometrica usuale, citando una selezione piuttosto curiosa di fonti per sostenere tale punto di vista. Tutto ciò suggerisce che il principale analista dell'epoca fosse sorprendentemente a disagio con i fondamenti.

Fu nel 1849 che Cauchy definì per la prima volta la nozione di continuità per una funzione complessa qualsiasi, anche se si trattava di una semplice generalizzazione del caso reale, e nel 1851 isolò come caratteristica che definisce una funzione complessa di x+iy quella di avere la derivata in ogni punto indipendente da dy/dx. Egli chiamò 'monogena' (il termine moderno è analitica od olomorfa) una funzione con tale proprietà. Nello stesso articolo enunciò un risultato simile al seguente: una funzione monogena definita su un disco aperto ammette, su esso, uno sviluppo in serie di potenze convergente. Egli aveva pubblicato la dimostrazione della proposizione inversa nel Mémoire di Torino del 1831. Insieme le due proposizioni stabiliscono l'equivalenza dei due approcci alla teoria delle funzioni complesse (quello basato sulle equazioni di Cauchy-Riemann e quello basato sulle serie di potenze convergenti). Cauchy aveva elaborato nel corso degli anni una teoria delle serie di potenze, ma spesso le sue affermazioni si sarebbero rivelate imprecise: l'enfasi era posta sulla continuità di una funzione, mentre era rilevante la sua differenziabilità, e la continuità della derivata veniva assunta tacitamente.

Cauchy rientrò definitivamente a Parigi nel 1838, dove stava emergendo una nuova generazione di matematici, alcuni dei quali avevano dato contributi nel campo dell'analisi complessa che, fino a quel momento, era stato suo quasi esclusivo appannaggio. Le interazioni non furono sempre facili: per gli altri non era semplice scoprire ciò che Cauchy aveva già pubblicato, e lui cedeva spesso alla tentazione di affermare di aver considerato da tempo le idee che essi proponevano.

La teoria di Cauchy si sviluppava intorno all'idea di considerare le funzioni analitiche in un disco. Abbastanza stranamente sembra che non gli fosse mai venuto in mente di trattare direttamente le funzioni con poli tagliando un piccolo disco contenente il polo e riducendo così il disco di partenza a un anello, o di cercare il prolungamento analitico in una regione anulare. Fu invece un ingegnere, Pierre-Alphonse Laurent (1813-1854), a concepire tale metodo in un lavoro presentato nel 1843 all'Académie sullo sviluppo in serie di potenze di una funzione definita e differenziabile in un anello. Laurent enunciò il suo teorema in completa generalità ma non ne diede una dimostrazione, limitandosi alla discussione di un caso particolare. L'articolo fu pubblicato solo nel 1863 dopo la morte dell'autore e per un certo periodo si seppe che era prossimo alla pubblicazione solo grazie alla recensione che ne aveva fatto Cauchy. Questi trovava che i risultati erano degni di considerazione, sebbene fossero già stati inclusi come "casi particolari" in alcuni dei suoi lavori precedenti. Pubblicò quindi una nota in cui diede la prima dimostrazione del teorema di Laurent (essenzialmente la dimostrazione moderna, utilizzando la formula integrale) che non aveva mai pensato di scrivere prima. Cauchy aveva considerato molte volte funzioni con poli e aveva anche calcolato il loro sviluppo in serie di Laurent, ma questo non gli aveva mai suggerito un teorema generale. L'ironia in tutto ciò si manifesta pienamente solo quando si passa a considerare il contributo di Karl Theodor Wilhelm Weierstrass (1815-1897).

Uno dei risultati principali della teoria delle funzioni di variabile complessa è un teorema che prende il nome da Joseph Liouville (1809-1882): una funzione definita su tutto il piano complesso e limitata è una costante. La storia di questo teorema segna l'avvento di una nuova generazione di matematici francesi, impegnati a superare un gigante proprio nel suo campo di ricerca. Liouville presentò il teorema in un articolo all'Académie nel 1846 in cui affermava, a proposito delle funzioni a un solo valore, che "se una tale funzione è doppiamente periodica e si riesce a provare che non diventa mai infinita, allora è possibile, solo da questo, dedurre che si riduce a una costante". Cauchy si affrettò ad affermare che il principio generale era conseguenza del suo lavoro precedente. Forse è davvero così, tuttavia il principio non era mai stato isolato né considerato da Cauchy prima che Liouville lo scoprisse indipendentemente e cominciasse a utilizzarlo. Cauchy fu anche il primo a fornire una dimostrazione del risultato in generale, utilizzando il suo teorema dei residui, arrivando a darne altre quattro nel 1847, mentre Liouville non ne pubblicò nessuna. Tutta questa attività mirava sicuramente a dare l'impressione che la scoperta di Liouville fosse già nota a Cauchy, ma Lützen ha dimostrato che Liouville aveva già isolato nel 1844 la proprietà per tutte le funzioni complesse e quindi sembra che l'attribuzione, almeno in questo caso, sia corretta.

Nel 1846 anche Liouville era un matematico all'apice delle sue capacità, responsabile di una propria rivista e con uno studente molto dotato, Charles Hermite (1822-1901), che lo spronava. Nel 1851, infastidito dalle affermazioni di Cauchy, Liouville decise di tenere un corso di pubbliche conferenze sul suo lavoro al Collège de France. Tra il pubblico erano presenti Charles-Auguste Briot (1817-1882) e Jean-Claude Bouquet (1819-1885) che, unificando ciò che avevano imparato da Cauchy sulla teoria delle funzioni di variabile complessa con l'approccio di Liouville alle funzioni doppiamente periodiche, scrissero nel 1859 la Théorie des fonctions doublement périodiques, il primo libro di testo sull'argomento. Cauchy era ormai morto, ed era cominciato un nuovo periodo di sviluppo nel campo dell'analisi complessa.

Nel loro libro, Briot e Bouquet definirono tre termini fondamentali: monodrome, che significa a un solo valore, monogène, che nella terminologia moderna si traduce con analitico, e synectique, che significa finito, continuo, monodrome e monogène in una regione del piano. I concetti sono tratti da Cauchy, insieme con la confusione tra continuo e differenziabile; il concetto di continuità viene introdotto nelle definizioni, quello di differenziabilità viene utilizzato nelle dimostrazioni. Segue poi una trattazione della teoria delle funzioni complesse ragionevolmente completa, anche secondo lo standard moderno. Il teorema integrale e la formula integrale di Cauchy sono dimostrati e utilizzati per lo sviluppo in serie di potenze delle funzioni analitiche. Viene proposta una teoria dei poli e delle serie di Laurent: un polo di ordine m, per il quale Briot e Bouquet non utilizzano alcun termine speciale, è un punto a in cui la funzione f(z) è infinita ma in cui il prodotto (z−a)^mf(z) è finito. Il comportamento di funzioni come e^1/z nell'origine o di e^z all'infinito era assai più problematico da trattare. Briot e Bouquet pensavano che le funzioni fossero ovunque definite e così arrivarono a enunciare teoremi i quali affermavano che le funzioni synectiques definite ovunque, infinito incluso, assumono ogni valore complesso. Autori successivi tentarono addirittura di difendere questo punto di vista con argomenti di passaggio al limite, ma sembra che nel 1859 Briot e Bouquet lo accettassero acriticamente, forse perché conduceva a una teoria molto nitida secondo la quale, come corollario del teorema di Liouville, una funzione definita su tutto il piano complesso assume ogni valore complesso.

La teoria delle funzioni di variabile complessa occupava circa 40 pagine, ed era seguita da materiale più difficile sulle equazioni differenziali nel dominio complesso che, d'altra parte, forniva le basi per una estesa trattazione della teoria delle funzioni ellittiche. Riunendo questi argomenti, Briot e Bouquet fornivano una chiara base concettuale per l'importante argomento delle funzioni ellittiche, che si amalgamava bene con la nuova teoria delle funzioni di variabili complesse. Questo sviluppo in parallelo sarebbe divenuto abituale per circa un secolo, fino a che la teoria delle funzioni complesse divenne troppo ampia per trovar spazio in un unico libro assieme alla più prestigiosa delle sue applicazioni.

Le funzioni a più valori costituivano uno degli argomenti familiari ai matematici del XIX sec., ma perfino Cauchy aveva difficoltà a trattarlo con precisione. La più semplice di queste funzioni è la radice quadrata: w²=z, o w=√z. Per ogni valore di z diverso da 0 (e da ∞) la funzione w assume due valori. Questo esempio poneva pochi problemi, essendo facilmente trattabile con tecniche ad hoc.

Per esempio, si può scrivere:

[3] z=re^iθ=re^i(θ+2π)

da cui

Se si prende z su un cerchio con centro nell'origine, e si fissa un corrispondente valore di w, è chiaro che quando si ritorna al punto di partenza il valore di w ha cambiato segno. Se questo è un problema, e in generale non lo è, si può immaginare di tagliare il piano lungo l'asse reale negativo, da 0 a −∞. Se si fa variare z su un qualsiasi cammino che non attraversa il taglio, il corrispondente valore di w non cambia segno. Questo metodo utilizzato da Cauchy è insegnato ancor oggi ed è adeguato allo scopo, ma è un modo troppo rozzo per trattare funzioni a più valori più complicate. Si basa sull'idea di tagliare il piano in un numero sufficiente di linee rette (chiamate da Cauchy lignes d'arrêt) in modo tale che w assuma sempre un solo valore fintantoché z non attraversi i tagli. In effetti quello che Cauchy sembra suggerire è che una funzione a più valori debba avere dei tagli (non semplicemente che è possibile assegnarle dei tagli).

Nel 1850 Puiseux pubblicò un altro metodo nella rivista di Liouville. In primo luogo distinse con cura tra poli (dove la funzione diventa infinita) e punti di diramazione (come l'origine per la funzione a più valori w²=z). Fissò quindi l'attenzione sulle permutazioni dei diversi valori di w quando z percorre un cerchio attorno a ognuno dei punti di diramazione e analizzò attentamente il modo in cui questo può accadere, descrivendo un metodo per risolvere completamente il problema in ogni caso. Non è necessario, per esempio, che i valori siano tutti permutati, ma dimostrò che sono tutti connessi, ovvero che è possibile muovere z lungo un cammino che congiunge una qualsiasi coppia fissata di valori di w. Per ogni punto di diramazione della funzione mostrò come ottenere uno sviluppo in serie di potenze con esponenti frazionari, e definì un metodo per calcolare questi esponenti (il metodo del poligono di Newton-Puiseux).

Dimostrò anche che è possibile trovare un cammino sul quale far muovere z in modo che sia z sia w ritornino ai loro valori originari senza però che il cammino di w possa essere contratto a un punto. Chiamò periodo l'integrale di w lungo questo cammino, per analogia con la teoria degli integrali ellittici, e valutò questo integrale in alcuni casi. Cauchy commentò favorevolmente il lavoro di Puiseux di fronte all'Académie, e in un'altra occasione attribuì a Puiseux il merito di essere stato il primo a chiamare cammino (chemin) un percorso di integrazione. L'uso delle matrici per descrivere come vengono permutati i punti di ramificazione si deve a Hermite.

Riemann

Georg Friedrich Bernhard Riemann (1826-1866) fu probabilmente la figura più importante nella matematica della seconda metà del XIX secolo. Malgrado la sua influenza dovesse rivelarsi così profonda, si dovettero attendere anni, addirittura decenni, per poter comprenderne tutte le implicazioni. In nessun altro dominio ciò risulta tanto evidente quanto nel suo preferito, quello della teoria delle funzioni di variabili complesse.

Nel periodo in cui era studente all'Università di Gottinga, Riemann cominciò a leggere i lavori di Cauchy e di Gauss, e mentre l'influenza del primo appare chiaramente in tutto ciò che in seguito scrisse, quella di Gauss è più difficile da individuare dal momento che i suoi contributi non erano organici, e alcuni furono inglobati per la prima volta nel corpo della teoria delle funzioni di variabili complesse da Riemann stesso. Trasferitosi all'Università di Berlino nel 1847, Riemann continuò a studiare i lavori di Gauss sulla teoria del potenziale, sul principio di Dirichlet e sulle applicazioni conformi. Riemann conosceva Gauss personalmente, ma fu senza dubbio Dirichlet, che riconobbe e incoraggiò il suo straordinario talento, a esercitare su di lui l'influenza maggiore. Quando nel 1851 Dirichlet visitò l'Università di Gottinga per un anno, lui e Riemann ebbero l'opportunità di discutere assieme quasi ogni giorno.

Il primo lavoro importante di Riemann fu la sua tesi di dottorato del 1851. Essa fu pubblicata, postuma, per la prima volta nella prima edizione dei Gesammelte matematische Werke (1876). Le poche copie stampate della tesi, distribuite nello stesso anno in cui venne discussa, erano di sicuro scarsamente note e difficili da trovare, e questo è probabilmente il motivo per cui vi è una notevole sovrapposizione con il lavoro del 1857 sulle funzioni abeliane. La dissertazione inizia con tre idee importanti: la definizione e le proprietà fondamentali di una funzione complessa, l'idea di superficie di Riemann, il ruolo fondamentale della teoria delle funzioni armoniche. Nell'articolo viene utilizzata una definizione informale di continuità, ma l'influenza di Dirichlet risulta evidente in alcune annotazioni che mostrano come Riemann basasse le sue idee di continuità sulla definizione 'epsilon-delta' del Cours d'analyse di Cauchy. La distinzione tra coppia di funzioni di due variabili reali e funzione complessa di una variabile complessa, che era costata a Cauchy tanti sforzi, fu colta immediatamente da Riemann: una variabile complessa w si dice funzione complessa di un'altra variabile complessa z se il valore di dw/dz, il limite del rapporto incrementale è indipendente dal valore del differenziale dz. Riemann osservò che questo si verifica ogni volta che le regole di differenziazione vengono applicate in maniera puramente formale. Dedicò il resto dell'articolo a definire le proprietà di cui gode una funzione complessa generale.

Innanzi tutto Riemann dimostrò che una funzione complessa è conforme, purché la sua derivata non si annulli, sottolineando così un'ipotesi che Cauchy non aveva mai esplicitato. Dimostrò inoltre che una funzione complessa f(x+iy)=u(x,y)+iv(x,y) soddisfa le equazioni di Cauchy-Riemann:

Da queste equazioni segue subito che le funzioni u e v sono armoniche (Riemann non introdusse però alcun termine specifico per questa proprietà); una funzione F di due variabili reali si dice armonica se soddisfa la relazione

Riemann si rese conto che la sua definizione di funzione complessa richiedeva soltanto che la funzione fosse definita su una famiglia di insiemi aperti bidimensionali. Tali insiemi si possono intersecare, ma non è necessario che la loro unione coincida con il piano complesso: altre superfici sono possibili. Tale intuizione gli consentì di considerare le funzioni a più valori, forse l'argomento che maggiormente aveva messo in difficoltà Cauchy, sostenendo che tali funzioni dovevano essere pensate come definite su superfici che si estendono sul piano della variabile z. In una tale superficie non sono ammesse pieghe, ma essa può avvolgersi intorno a certi punti, che Riemann chiamò 'punti di diramazione'. Cosa si intendesse per intorno di un punto di diramazione non era spiegato in modo chiaro.

Nel dicembre del 1851 Riemann aveva già letto la relazione di Cauchy sulla memoria di Puiseux, tuttavia sembra improbabile che questa abbia avuto qualche influenza sulla sua tesi di dottorato. Il concetto di superficie di Riemann doveva risultare ostico da padroneggiare per i matematici successivi, non da ultimo perché presenta la superficie come qualcosa che si estende sopra l'intero piano complesso, in un modo che dipende da quattro dimensioni reali. Riemann cercava di rappresentare una superficie divisa in parti maneggevoli per mezzo di tagli. Diceva 'connessa' una parte di superficie quando, per ogni coppia di punti in essa contenuti, esisteva una curva che li congiungeva. Riemann sezionava le superfici per mezzo di tagli lungo cicli, curve semplici (non intrecciate) con gli estremi sul bordo; tagli preesistenti di questo genere contano anche loro come parti del bordo ed era possibile scegliere un punto arbitrario della superficie come punto del bordo da cui iniziare il processo di dissezione. Una superficie si dice 'semplicemente connessa' se ogni taglio lungo un ciclo la divide in due pezzi e 'n-volte connessa' se è necessario un sistema di n−1 tagli lungo i cicli per renderla semplicemente connessa.

Per studiare le funzioni complesse, Riemann utilizzò la teoria delle funzioni armoniche con punti singolari. Il teorema fondamentale su cui fondava il suo studio è una versione del teorema di Green già nota a Cauchy e Gauss (senza dubbio la fonte di Riemann, forse attraverso Dirichlet). Esso mette in relazione un integrale di superficie con un integrale lungo il bordo della superficie stessa. Riemann dimostrò questo teorema e lo utilizzò per dimostrare che una funzione armonica u con punti singolari isolati possiede derivate di ogni ordine, un passo fondamentale verso l'unificazione della teoria delle funzioni complesse con quella delle funzioni armoniche. Esso implica che una funzione complessa w=x+iy è infinitamente differenziabile, perché lo sono la parte reale e la parte immaginaria. Riemann considerò quindi la teoria dello sviluppo in serie di Laurent nell'intorno di un polo di ordine finito e la teoria dei punti di diramazione.

Nella seconda parte della sua tesi forniva poi una dimostrazione del fatto che due superfici piane semplicemente connesse si possono sempre trasformare l'una nell'altra con una applicazione conforme e che tale applicazione è unica una volta fissate l'immagine di un punto interno arbitrario e quella di un punto del bordo, anch'esso arbitrario. Questo risultato, oggi chiamato 'teorema di rappresentazione di Riemann' ed enunciato in maniera leggermente diversa, stabilisce che due qualsiasi regioni semplicemente connesse sono equivalenti ai fini della teoria di Riemann delle funzioni complesse e quindi, in particolare, che esistono funzioni complesse definite su ognuna di esse.

Si afferma spesso che la dimostrazione di Riemann si basa in modo essenziale sul principio di Dirichlet, e che per questa ragione non fu accettata da molti matematici. In verità però l'approccio di Riemann era alquanto differente. Egli non si limitava ad applicare in maniera ingenua il principio di Dirichlet, secondo il quale se è assegnata una funzione continua sul bordo di una regione semplicemente connessa, allora esiste una funzione armonica definita sull'intera regione che coincide con la funzione data sul bordo. Nel 1857 Riemann spiegò che nella sua dissertazione aveva cercato di generalizzare il principio di Dirichlet al caso in cui venissero ammesse determinate discontinuità. La funzione armonica da prendere in considerazione è la funzione che minimizza un certo integrale. Permaneva una confusione diffusa tra l'esistenza di un estremo inferiore per l'integrale (mai messa in dubbio) e quella di una funzione che realizza tale estremo. Riemann cercò di dimostrare il risultato di esistenza argomentando che l'integrale è funzione continua dell'espressione integranda, e che questi ingredienti formano quello che egli descriveva come un "dominio connesso chiuso in sé stesso". Dal momento che gli ingredienti sono essi stessi funzioni, l'affermazione risulta audace, ma non si tratta di un uso ingenuo del principio euristico di Dirichlet. Purtroppo, come altri non tardarono a osservare, l'argomento di Riemann è fatalmente carente sotto altri punti di vista.

L'intero approccio di Riemann si basa su questo risultato. Secondo le sue stesse affermazioni, questi principî "aprono la via a uno studio delle funzioni di una variabile complessa che non dipende da una loro espressione esplicita" (Riemann 1851, par. 19). Un simile punto di vista determinò una rottura completa con l'idea che la teoria delle funzioni complesse avesse essenzialmente a che fare con espressioni formali come le serie di potenze e semplificò enormemente il compito di decidere quando due espressioni rappresentano la stessa funzione; per esempio, è chiaro ‒ affermava Riemann ‒ che se una funzione è ovunque definita su una regione che ricopre l'intero piano una o più volte, e ha singolarità solo di ordine finito e solo in un numero finito di punti, allora è una funzione algebrica.

Nell'articolo del 1857, pubblicato nel "Journal" di Crelle, Riemann prendeva in esame un problema centrale della matematica di quel periodo, l'oscura teoria delle funzioni abeliane e, dopo aver illustrato ancora una volta il suo approccio alle funzioni complesse, mostrava come gli integrali su una superficie possano essere indipendenti dal cammino che congiunge i loro estremi.

Il principale oggetto di studio era la teoria delle funzioni su una curva algebrica. La curva era concepita in due modi che Riemann cercò di amalgamare senza molto successo: quale oggetto definito da una equazione irriducibile tra le variabili complesse s e z di gradi n in s e m in z; e come oggetto rappresentato da un rivestimento T a n fogli del piano della variabile z. Le funzioni razionali di s e z sono funzioni a un solo valore su T, ramificate come s. Nello stesso articolo Riemann dimostrò anche la proposizione inversa. L'integrale di una funzione razionale produce una funzione a più valori i cui diversi prolungamenti analitici differiscono soltanto per una costante, poiché le derivate devono coincidere punto per punto. Era questo sistema di funzioni che egli proponeva di studiare utilizzando il principio di Dirichlet e la propria tecnica di sezionare la superficie con 2p tagli per poterla distendere sul piano e trasformarla in una superficie semplicemente connessa T′.

Le più semplici sono le funzioni w a più valori ovunque finite. Riemann mostrò, considerando i loro incrementi nell'attraversamento dei tagli, che ci sono al più p funzioni linearmente indipendenti siffatte, w₁,…,w^p. Sul modello della classificazione degli integrali ellittici, furono chiamate da Riemann 'integrali del primo tipo' e si ottengono integrando espressioni ovunque olomorfe. Si devono considerare poi funzioni con un polo di ordine superiore in un singolo punto, denominate da Riemann 'integrali del secondo tipo', che si ottengono dall'integrazione di funzioni razionali prive di poli semplici e che egli denotava con b_jt_j. Infine esistono funzioni con due poli logaritmici, uguali ma opposti, che furono chiamate 'integrali del terzo tipo' e si ottengono integrando funzioni con poli semplici aventi residui opposti.

Così, sosteneva Riemann, l'espressione generale per una funzione complessa con m poli semplici su una superficie è della forma

[7] s=b₁t₁+b₂t₂+…+b_mt_m+a₁w₁+a₂w₂+…+a_pw_p+cost,

dove i valori delle t sono arbitrari e quelli di a_i e b_j sono costanti. Se tutti gli incrementi nell'attraversare i 2p tagli (chiamati da Riemann 'moduli di periodicità') svaniscono, la funzione è a un solo valore. Con semplici ragionamenti di algebra lineare stabilì che essa dipende linearmente da m−p+1 costanti arbitrarie. Se questo numero è più grande di 1, cioè se m>p, esistono funzioni non costanti con al più m poli. Questa è la celebre 'disuguaglianza di Riemann'. La sua principale applicazione consiste nel definire l'esistenza di funzioni razionali su una superficie di Riemann.

Egli dimostrò successivamente che funzioni razionali distinte e non costanti soddisfano un'equazione polinomiale che si può assumere come l'equazione di una superficie di Riemann, stabilendo in questo modo una connessione tra i suoi due approcci all'argomento. Infine osservò che se w è una qualsiasi funzione definita su T avente solo poli semplici, allora dw/dz è un'altra funzione dello stesso tipo. In particolare essa può avere solo poli nei punti in cui li ha la funzione w. Perciò tutte le funzioni definite su T o hanno le stesse diramazioni di T oppure sono integrali di funzioni siffatte. Inoltre, il sistema di queste funzioni è determinato quando è assegnata la superficie T e dipende soltanto dalla posizione dei punti di diramazione.

Uno dei meriti dell'approccio di Riemann è l'aver chiarito come la stessa superficie di Riemann si possa rappresentare per mezzo di molte equazioni diverse, ottenibili le une dalle altre attraverso una trasformazione razionale delle variabili. Egli fu in grado di dimostrare che la famiglia delle superfici non equivalenti di un dato genere dipende con continuità da 3p−3 parametri complessi che, affermava, "verranno detti moduli". Da allora lo spazio dei moduli ha continuato a suscitare grande interesse. Con un altro breve argomento Riemann dimostrò che esiste uno spazio, dipendente da un parametro, di tutte le superfici di Riemann di genere uno.

La seconda metà dell'articolo è dedicata allo studio delle funzioni razionali e algebriche su una data superficie di Riemann e sarà discussa in seguito. La profonda originalità di questo importante lavoro si può rilevare dal fatto che nel leggerlo un'autorità del livello di Weierstrass decise di rinviare la pubblicazione di uno scritto sullo stesso argomento, preferendo prima assimilare quello che Riemann aveva affermato.

Riemann, la cui già precaria salute si era definitivamente aggravata nel 1862 a causa della tubercolosi, trascorse quasi sempre in Italia gli ultimi quattro anni di vita, incontrando numerosi matematici italiani. I suoi studi furono pubblicati postumi soltanto nel 1876 da Richard Dedekind (1831-1916) e Heinrich Weber (1842-1913) che ne curarono un'edizione nella quale la maggior parte dei risultati raggiunti dal matematico tedesco era presentata per la prima volta. Le idee di Riemann si diffusero anche attraverso il lavoro dei pochi che avevano assistito alle sue lezioni o che l'avevano conosciuto personalmente. Poiché si dice spesso che le reazioni immediate all'opera di Riemann furono scarse, può essere interessante fornirne una panoramica, anche se parziale. Mentre egli era ancora in vita, nel 1863 Alfred Clebsch (1833-1872) riprese il concetto di genere, il teorema di Abel e l'uso delle funzioni abeliane in geometria; Gustav Roch (1864) raffinò la disuguaglianza di Riemann in una uguaglianza; Carl Gottfried Neumann (1832-1925) scrisse le Vorlesungen über Riemann's Theorie der Abel'schen Integrale (Lezioni sulla teoria di Riemann degli integrali abeliani, 1865), sull'approccio di Riemann agli integrali iperellittici; Jacob Heinrich Karl Durège, nel 1865, basò sulle idee di Riemann il primo libro in tedesco riguardante la teoria delle funzioni di variabile complessa; numerosi autori, fra i quali Clebsch, Jacob Lüroth, Jakob Rosanes e William K. Clifford, fecero chiarezza su alcuni problemi riguardanti la comprensione della topologia di una curva algebrica; Clebsch e Paul A. Gordan (1837-1912) dedicarono il volume Theorie der Abelschen Funktionen (1866) alla teoria delle funzioni abeliane. Dopo la sua morte, negli anni Sessanta del XIX sec., Friedrich Emil Prym, Elwin Bruno Christoffel e Hermann Amandus Schwarz lavorarono al teorema di rappresentazione di Riemann; Felice Casorati pubblicò nel 1868 la Teorica delle funzioni di variabili complesse, una presentazione esplicitamente riemanniana della teoria delle funzioni complesse; Hermann Friedrich Schottky estese il teorema di rappresentazione di Riemann a domini non semplicemente connessi; Alexander Wilhelm von Brill e Max Noether pubblicarono nel 1872 uno studio sulle curve algebriche nel quale il teorema di Riemann-Roch veniva chiamato per le prima volta con questo nome; Leonida Tonelli nel 1875 scrisse un articolo sulla definizione di Riemann di genere. Verso la fine degli anni Settanta del XIX sec. Weierstrass ne diede una nuova definizione e ricavò il cosiddetto 'teorema delle lacune'.

Questo elenco, benché parziale, e il contemporaneo sforzo di curare l'edizione degli articoli ancora inediti, delle dispense dei corsi e dei frammenti, indicano una volontà reale di mantenere vive le idee di Riemann dopo la sua prematura scomparsa. Il mondo accademico aveva riconosciuto da tempo il suo talento. Weierstrass aveva caldeggiato con forza la candidatura di Riemann alla Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino nel 1859, negli anni successivi aveva incoraggiato i suoi studenti migliori a cercare negli scritti di Riemann buoni argomenti sui quali lavorare dimostrando l'importanza e il rigore che erano essi riconosciuti.

La sua teoria delle funzioni di variabili complesse si fonda su pochi punti fondamentali: l'importanza della natura globale del dominio di una variabile complessa e la sua analisi topologica; il principio di Dirichlet per stabilire l'esistenza di funzioni complesse con singolarità prestabilite; la disuguaglianza di Riemann. L'accettazione di ognuno di questi punti era problematica anche per i migliori tra i suoi contemporanei.

Volendo considerare il caso più famoso ‒ l'uso di Riemann del controverso principio di Dirichlet ‒ negli anni Ottanta del XIX sec., Christian Felix Klein (1849-1925) cercò di argomentare che Riemann avesse fatto ricorso al principio di Dirichlet sulla base di considerazioni di natura fisica; ma Umberto Bottazzini ha mostrato che alcuni studenti di Riemann, in particolare Prym, non erano d'accordo. Di fatto, mentre da un lato i matematici ritenevano che il principio richiedesse una dimostrazione, dall'altro fisici come Hermann von Helmholtz (1821-1894) e James C. Maxwell (1831-1879) non erano d'accordo. Solo nel 1900 David Hilbert (1862-1943) riuscì a dare una dimostrazione diretta della validità del principio di Dirichlet per un'ampia classe di domini, ripristinando così l'originale linea di pensiero di Riemann sotto ipotesi appena più restrittive.

Comunque, la ricerca di dimostrazioni condusse una generazione di matematici ad allontanarsi spesso dalla visione di Riemann; Clebsch, suo successore a Gottinga, era il leader di un forte gruppo di geometri algebrici che cercarono di riscrivere le idee di Riemann nel linguaggio della geometria proiettiva delle curve algebriche e di ritornare all'analisi attraversando il ponte, come essi lo chiamavano, fornito dal teorema di Abel. Prym scrisse a Casorati che il libro di Clebsch e Gordan era "completamente inutile". Ciò che lo disturbava era l'enfasi posta sull'algebra a scapito della topologia. Pur se in modo imperfetto, Riemann aveva tentato di separare la superficie, pensata come oggetto astratto, da ogni sua immersione in un qualsiasi spazio proiettivo complesso; la trattazione di Clebsch-Gordan cercava di eliminare quella distinzione. Analogamente perentorio fu Roch nel giudicare 'poltiglia ribollita' la prima edizione delle Vorlesungen über Riemann's Theorie di Neumann. Curiosamente, quando la seconda edizione venne letta a Gottinga, Klein affermò che essa faceva apparire ogni cosa così semplice da sembrare quasi un insulto. Evidentemente, a Gottinga almeno, i matematici avevano cominciato a confrontarsi con Riemann. Solo Casorati ebbe successo con la Teorica delle funzioni di variabili complesse che mescolava le tecniche e le idee di Cauchy, Riemann e Weierstrass, e che favorì la diffusione in Italia della teoria riemanniana delle funzioni. La prima parte di questo testo tratta lo studio delle superfici di Riemann e delle funzioni abeliane, la seconda, più elementare, presenta invece gli argomenti che Riemann stesso aveva trattato nelle sue lezioni.

Il successo in Italia, dove molti matematici avevano conosciuto Riemann personalmente, non deve nascondere i problemi che si presentano altrove. Weierstrass e i suoi studenti erano avversi allo spirito riemanniano e in Francia Hermite ne ritardò l'accettazione per almeno una generazione, per essere poi superato da Jules-Henri Poincaré (1854-1912) e Charles-Émile Picard (1856-1941). Anche a Gottinga, dove Klein si adoperò per tener viva la teoria riemanniana delle funzioni, la prima trattazione soddisfacente delle superfici di Riemann fu data da Hermann Weyl (1885-1955) soltanto nel 1913.

Weierstrass

Una caratteristica notevole dell'approccio di Weierstrass all'analisi complessa consiste nell'evitare l'uso di integrali, il che è coerente con l'idea di non attribuire alle equazioni di Cauchy-Riemann un ruolo fondamentale. Weierstrass giustificava tale scelta osservando che "le condizioni per l'esistenza di una derivata sono così complicate che, a priori, non è assolutamente possibile verificare se una data funzione ammetta derivate, a meno che non lo si sappia per esperienza" (Weierstrass 1988, p. 115). Egli costruì così una teoria delle funzioni definite per mezzo di serie uniformemente convergenti di funzioni razionali su un dato dominio. Come è stato mostrato, questo approccio procurò a lui e ai suoi seguaci molte difficoltà. Una consisteva nella dimostrazione dell'esistenza e unicità dello sviluppo in serie di Laurent di una funzione analitica su un anello. La dimostrazione usuale di esistenza, come quella fornita dallo stesso Weierstrass del 1841, faceva uso del teorema integrale di Cauchy e Weierstrass non riuscì mai a eludere questa difficoltà (nelle sue lezioni si limitava a dire "È ben noto che…"). Nel 1884 furono pubblicate due dimostrazioni che evitavano completamente l'integrazione, una di Georg Scheffers (1866-1945) e l'altra di Gustaf Mittag-Leffler (1846-1927). Nel 1896 una dimostrazione fu elaborata anche da Alfred Pringsheim (1850-1941). Altri problemi riguardavano la dimostrazione del teorema delle singolarità eliminabili e del teorema di Liouville. Weierstrass fu in grado di superare questi ostacoli, tuttavia perfino gli allievi trovavano i suoi argomenti difficili, e a chiunque non condividesse l'idea di considerare elementare la convergenza uniforme ma non la teoria dell'integrazione, questo modo di procedere appariva astruso. Le continue dispute sorte a Berlino sulla natura della matematica, ebbero intensità sempre crescente. Il punto di vista di Weierstrass sui fondamenti dell'analisi complessa non era condiviso da Leopold Kronecker (1823-1891), che basava sul teorema integrale di Cauchy e sulla formula integrale di Cauchy le sue lezioni sulla teoria delle funzioni di variabile complessa, affermando in proposito che l'intera teoria moderna delle funzioni era concentrata in questi due integrali.

Caratteristico della concezione di Weierstrass era il desiderio di costruire una teoria veramente elementare delle funzioni di variabili complesse, priva di ogni assunzione ed esente da circoli viziosi. In questo modo di procedere egli ricordava Euclide più di ogni altro matematico dell'epoca. In parte conseguenza della sua posizione di direttore del più grande e importante istituto di matematica del mondo, tale atteggiamento rifletteva anche il suo personale desiderio di uniformità e di rigore. Come Euclide, Weierstrass fornì scarse indicazioni sugli altri approcci alla materia, dando così l'impressione di ritenerli carenti perché non si armonizzavano con il suo approccio globale. Egli rifletteva a lungo e con grande attenzione sul giusto grado di generalità con cui considerare un problema o un concetto e amava saggiarne tutte le implicazioni e le conseguenze prima di includerlo nel suo ciclo di lezioni. Pertanto si devono a lui molte delle distinzioni fondamentali della teoria, che hanno contribuito indubbiamente a chiarire il materiale che si andava accumulando.

Un problema sollevato da Riemann era se ogni funzione complessa, definita alla sua maniera astratta, coincidesse con una funzione definita algebricamente. Nonostante egli riconoscesse tale coincidenza, i matematici berlinesi risolsero negativamente la questione. Le serie di funzioni razionali si possono comportare in maniera molto diversa dalle serie di potenze. Per esempio, la serie ∑1/(zⁿ+z⁻ⁿ) converge per ∣z∣>1 e per ∣z∣⟨1, ma non quando ∣z∣=1. Infatti il cerchio definito dalla condizione ∣z∣=1 è quella che si dice una frontiera naturale per le funzioni definite al suo interno e al suo esterno: una non può essere prolungata analiticamente nell'altra. Così una stessa espressione algebrica definisce due funzioni distinte, in contrasto con le convinzioni di Riemann.

Le frontiere naturali che impediscono a una funzione di variabile complessa definita su un disco di essere prolungata all'intera sfera di Riemann, sono composte da punti in ogni intorno dei quali la funzione ha almeno un polo (e pertanto non può essere definita). Per comprenderne la natura furono impegnate molte energie. In conseguenza del teorema di rappresentazione di Riemann le frontiere naturali possono avere una grande varietà di forme. Anche quando sono cerchi possono essere costituite soltanto da poli, o avere un insieme denso di poli, o non averne affatto (esempi di tali frontiere sono facili da trovare). Un caso celebre è dato dalle funzioni ellittiche, in particolare dalla funzione

con ∣q∣⟨1, introdotta da Carl Gustav Jacob Jacobi (1804-1851), che ha come frontiera naturale il cerchio unitario. Può sembrare che questa funzione ne definisca una reale sul cerchio unitario, ma Weierstrass si rese conto che, in tal caso, la funzione avrebbe dovuto avere proprietà notevoli. Analizzandola, egli fu condotto a studiare una funzione leggermente diversa che risultò essere ovunque continua e mai differenziabile. Essa fu la prima funzione di questo tipo definita rigorosamente e aprì la strada alla comprensione della grande diversità dei concetti di continuità e differenziabilità.

All'estremo opposto, la più semplice frontiera naturale che una funzione possa avere è un singolo punto, e anche in questo caso il problema è sottile. Se la frontiera naturale consiste di un polo, o anche di molti poli in punti distinti, la funzione è razionale. Tuttavia nel 1875 Weierstrass scoprì che esiste una differenza cruciale tra un punto che rappresenta un polo di ordine finito e quella che in seguito al suo lavoro venne chiamata una 'singolarità essenziale', dove non è definita né la funzione né la sua reciproca. Weierstrass scoprì che in ogni intorno di una singolarità essenziale la funzione assume valori arbitrariamente vicini a ogni numero complesso. In effetti, come avrebbe dimostrato Picard nel 1879, in ogni intorno di una singolarità essenziale la funzione assume ogni valore finito, eccetto al più uno.

Weierstrass si occupò anche del problema inverso: assegnato un insieme di punti, se esiste una funzione che ammette poli oppure singolarità essenziali precisamente in quei punti. L'insieme non può avere un punto di accumulazione, altrimenti la funzione si annullerebbe identicamente. Inoltre egli fece l'ipotesi che ci fosse solo un numero finito di singolarità essenziali. Nel 1875 Weierstrass dimostrò che non sono necessarie altre restrizioni e fornì convenienti espressioni esplicite per le funzioni cercate nella forma di prodotti infiniti (analoghe all'espressione determinata da Euler per la funzione seno), ispirandosi al prodotto infinito definito per la funzione gamma di Euler e Gauss. Le sue idee vennero riprese da Mittag-Leffler, che aveva seguito le lezioni di Weierstrass del 1875. Mittag-Leffler dimostrò che esiste sempre una funzione meromorfa con parti principali specificate (espressioni della forma

∑ⁿi₌₁a_i /(z-a)ⁱ ).

Funzioni ellittiche e funzioni abeliane

La teoria delle funzioni ellittiche, una branca ben sviluppata della matematica, esercitava un'influenza decisiva sulla teoria delle funzioni di variabile complessa, e quest'ultima prometteva di approfondirla e di semplificarla. Essa emerse da quello che era stato, a partire dal 1790 ca., uno degli interessi costanti di Adrien-Marie Legendre che per quarant'anni aveva pubblicato libri e articoli sugli integrali ellittici, un argomento che da lungo tempo occupava un posto ben definito nell'astronomia dell'epoca, nella quale con tali integrali si calcolava la lunghezza d'arco lungo un'orbita ellittica. Negli Exercises de calcul intégral (1817) e nel Traité des fonctions elliptiques et des intégrales eulériennes (1827) Legendre li pose in relazione con molti problemi, tra i quali la rotazione di un solido attorno a un punto fisso, l'attrazione esercitata da un ellissoide omogeneo, il moto rispetto a forze centrali e la determinazione delle geodetiche di un ellissoide. Il Traité di Legendre è una presentazione sistematica di nuove funzioni di una variabile reale che comprende la loro definizione e le loro proprietà fondamentali, e ne tabula i valori dei quali mostra l'utilità nel risolvere problemi significativi di matematica applicata.

Legendre si adoperò attivamente affinché nel 1830 l'Académie des Sciences di Parigi assegnasse il Grand Prix della matematica a Jacobi di Königsberg, allora venticinquenne, e alla famiglia di Niels Henrik Abel di Christiania, morto l'anno prima all'età di 26 anni; essi non soltanto avevano esteso le sue idee, ma le avevano completamente riformulate invertendo gli integrali (possibilità intuita da Legendre che non ne aveva saputo riconoscere il valore) e considerando estremi di integrazione complessi (Legendre non lo aveva mai fatto). L'inversione è un processo familiare nella trigonometria. L'integrale

definisce la funzione a più valori u(v)=arcsenv, che a sua volta si può utilizzare per definire, prendendone l'inversa, la funzione v=senu. Allo stesso modo l'integrale ellittico più semplice e paradigmatico è

che misura la lunghezza d'arco della lemniscata r²=cos2θ, una curva che ha la forma di un otto. La [9] definisce una funzione a più valori u(v), che si può utilizzare per definire, prendendone l'inversa, una funzione doppiamente periodica v(u), che Gauss chiamò sl(v) (sinus lemniscatus).

La ragione per estendere questa funzione a valori complessi di v sta in un'apparente mancanza di analogia con le funzioni trigonometriche. L'equazione per la trisezione di un angolo senx=sen(a/3) ha tre soluzioni distinte per x in corrispondenza di ogni valore assegnato di a, mentre la corrispondente equazione per sl(v) ne ha nove. Questo suggerì a Gauss, Abel e Jacobi, ma non a Legendre, che le radici in più potessero essere complesse e quindi che si dovesse considerarla come una funzione complessa.

Tuttavia, nel 1830, la teoria delle funzioni di variabile complessa era poco sviluppata per potervi attingere e anche nei lavori di Cauchy mancava la trattazione degli integrandi a più valori (come le radici quadrate negli integrali ellittici). La teoria creata da Abel e Jacobi doveva però favorire lo sviluppo della teoria delle funzioni di variabile complessa. Essi dimostrarono che le funzioni ottenute invertendo l'integrale ellittico generale

(per valori reali dei parametri c ed e) sono interessanti e comprensibili generalizzazioni delle funzioni trigonometriche. Tali funzioni verificano, per esempio, leggi di addizione analoghe a quelle della funzione seno e vennero estese da valori reali a valori complessi della variabile; questi sviluppi erano tuttavia completamente formali e si sarebbero rivelati per certi versi infondati.

L'entusiasmo che fece seguito ai lavori di Abel e Jacobi non turbò Gauss, il quale dichiarò che Abel aveva percorso "circa un terzo della strada". Questa osservazione inaspettata venne alla luce soltanto con la pubblicazione postuma dei suoi quaderni. Uno dei problemi che Gauss aveva risolto riguarda la definizione delle funzioni [10] per valori complessi di c e di e, che gli permise di dimostrare che le funzioni doppiamente periodiche più semplici, dalle quali si possono costruire algebricamente tutte le altre, sono funzioni ellittiche, e viceversa. Gauss era anche arrivato a una migliore comprensione del ruolo che spetta alle equazioni differenziali ordinarie lineari nella teoria delle funzioni ellittiche. Entrambi i successi sono dovuti alla natura essenzialmente geometrica della teoria delle funzioni di una variabile complessa di cui Gauss disponeva.

Intorno al 1840 altri matematici, tra i quali Cauchy e Arthur Cayley (1821-1895), cominciarono gradualmente a pubblicare le idee che Gauss teneva per sé. Successivamente, come è stato già osservato, Liouville dimostrò ‒ esemplificando così il vantaggio di applicare la teoria generale delle funzioni alle funzioni ellittiche ‒ che ogni funzione doppiamente periodica ha almeno due poli nel parallelogramma dei periodi, mentre Briot e Bouquet scrissero un intero libro fondando lo studio delle funzioni ellittiche sulla teoria delle equazioni differenziali complesse. In seguito, la maggior parte degli autori ritenne naturale sviluppare contemporaneamente le due teorie. Il punto di partenza per la teoria delle funzioni ellittiche divenne così un aspetto della teoria più ampia e generale delle funzioni di variabile complessa, che nel suo sviluppo giunse a inglobare la connessione con gli integrali ellittici. Questo abbinamento divenne talmente importante che la maggior parte degli autori del XIX sec. parlava di 'teoria delle funzioni' come della teoria delle funzioni di variabile complessa.

Gli integrali ellittici sono integrali di forma semplice che non si possono esprimere utilizzando le funzioni note nel XIX sec., ma esiste anche una vasta classe di integrali che non si può esprimere utilizzando le funzioni ellittiche. Anch'essi provengono da qualcosa che non è più complicato dei polinomi. Sono gli integrali della forma

[11] ∫F(x,y)dx,

nei quali le variabili (reali o complesse) soddisfano un'equazione del tipo G(x,y)=0, con F e G funzioni razionali di x e y. Si ottiene un integrale ellittico quando G(x,y)=y²−f(x), con f(x) polinomio di grado quattro e F(x,y)=1/y. In generale si assume che il polinomio G sia assegnato e F sia variabile; i matematici di orientamento geometrico parlavano dell'integrazione di funzioni definite sulla curva di equazione G(x,y)=0.

Le difficoltà nella comprensione di questi integrali furono utilmente chiarite da Abel in un'importante memoria pubblicata nel 1841, 12 anni dopo la sua morte, quando Jacobi, venuto a conoscenza della sua esistenza, spronò l'Académie a cercarla nei suoi archivi. Jacobi la chiamava monumentum aere perennius di Abel. Le funzioni introdotte in questa memoria sono dette ancor oggi 'funzioni abeliane' e differiscono da quelle ellittiche per un aspetto cruciale. Abel dimostrò l'esistenza di un numero naturale p, determinato da G, tale che la somma di un numero qualsiasi di integrali abeliani si possa scrivere come somma di esattamente p di loro. Nel caso degli integrali ellittici, p=1, l'inversione è facile. Tuttavia quando p>1, Abel dimostrò che la situazione è molto più complicata e Jacobi riuscì ad approfondirla pienamente. Nel caso più semplice si assume che negli integrali [11] compaiano integrande ovunque olomorfe. Esistono p integrali linearmente indipendenti di questo tipo:

[12] ∫F_j(x,y)dx, (j=1,2,...,p).

Per ognuno di essi si consideri la somma di p integrali ottenuta fissando arbitrariamente un punto iniziale x₀, e p punti finali x₁,...,x_p:

o meglio, si consideri la p-pla di tali integrali:

Questo oggetto, a prima vista intrattabile, è una funzione dei p numeri x₁,...,x_p, e il suo valore è un'altra p-pla di numeri, diciamo y₁,...,y_p. La scoperta di Abel e Jacobi è che la funzione inversa, che esprime x₁,...,x_p come funzione di y₁,...,y_p è una funzione 2p volte periodica di p variabili.

I matematici rimasero a lungo sconcertati da queste funzioni e ciò che procurò a Weierstrass la sua fama internazionale, assicurandogli una posizione accademica a Berlino, fu il fatto di essere riuscito per primo a fornirne una trattazione dettagliata nel caso speciale (detto 'iperellittico') in cui la funzione G(x,y) è della forma y²−p(x), con p(x) polinomio in x. In seguito, nel 1857, Riemann utilizzò la sua teoria delle funzioni di variabili complesse per generalizzare la teoria di Jacobi delle 'funzioni teta' al caso di più variabili, dando così la prima trattazione generale delle funzioni abeliane.

Nonostante questi sviluppi, le difficoltà tecniche nello studio delle funzioni abeliane rimasero formidabili e molto di quello che è stato scritto è un tributo alla forza dell'ingegno analitico. Ciò che mancava era una teoria delle funzioni di più variabili complesse capace di far luce sul problema nello stesso modo in cui la teoria delle funzioni di una singola variabile complessa aveva semplificato la trattazione delle funzioni ellittiche. Questa lacuna era avvertita acutamente e alcuni matematici, fra i quali Weierstrass e Poincaré, cercarono di porvi rimedio, anche se il conseguimento di successi parziali fu accompagnato da fallimenti notevoli.

Non esiste una generalizzazione semplice delle equazioni di Cauchy-Riemann al caso di più variabili: si ottengono più equazioni che variabili e manca un'intima connessione tra funzioni analitiche e funzioni armoniche. Nella teoria di una variabile il teorema di rappresentazione di Riemann stabilisce i domini possibili per una funzione, ma non si è stati in grado di trovare un risultato analogo nel caso di più variabili. Per una variabile il concetto di punto singolare è ricco di implicazioni e la distinzione tra poli e singolarità essenziali è cruciale. Ancora nel 1900 si poteva dire molto meno nel caso di più variabili. Le difficoltà sono illustrate da una funzione semplice come x/y, che non somiglia a una funzione con una singolarità essenziale ma la cui reciproca è diversa da zero. Nel caso di una sola variabile c'è un teorema importante di Cauchy su integrali e residui; per più variabili la situazione è stata chiarita intorno al 1880, e solo parzialmente, da alcuni risultati di Poincaré e di Picard.

Fu possibile sviluppare una teoria locale delle funzioni di più variabili complesse utilizzando le serie di potenze in più variabili con le relative regioni di convergenza, ma anche il semplice risultato che tali funzioni sono precisamente quelle separatamente analitiche in ogni variabile è stato dimostrato in modo rigoroso soltanto nel 1905. Lo sviluppo della teoria fu fortemente rallentato dal fallimento dei tentativi di trattare le singolarità, in particolare di definire e chiarire la natura delle singolarità essenziali, che nel caso di una variabile possono risultare isolate o, formando un insieme denso, essere la frontiera naturale della funzione. Nel 1880 Weierstrass affermò che anche le funzioni di più variabili possono avere singolarità essenziali isolate, un errore corretto dal matematico italiano Eugenio Elia Levi nel 1910 e che rivela le grandi difficoltà presenti in questo campo. Anche la semplice osservazione che una funzione analitica di più variabili non può avere una singolarità ordinaria in un punto isolato, che si dimostra considerando la sua espansione in serie di Laurent, sembra sia stata fatta per la prima volta da Adolf Hurwitz (1859-1919) solamente nel 1897.

Analoghe difficoltà riguardavano i tentativi di generalizzare direttamente la teoria delle funzioni ellittiche e delle loro funzioni teta. Per giungere a risultati definitivi in questo senso si dovette attendere fino al XX secolo. Sembra che in quegli anni la caratteristica peculiare di questa branca della matematica fosse la sua complessiva mancanza di successi, piuttosto che una qualsiasi delle sue sofferte vittorie.

Bibliografia

Belhoste 1991: Belhoste, Bruno, Augustin-Louis Cauchy. A biography, translated by Frank Ragland, New York-Berlin, Springer, 1991 (ed. orig.: Cauchy 1789-1857. Un mathématicien légitimiste au XIXème siècle, Paris, Belin, 1988).

Bottazzini 1986: Bottazzini, Umberto, The higher calculus. A history of real and complex analysis from Euler to Weierstrass, translated by W. von Egmond, Berlin-New York, Springer, 1986 (ed. orig.: Il calcolo sublime. Storia dell'analisi matematica da Euler a Weierstrass, Torino, Boringhieri, 1981).

Freudenthal 1991: Freudenthal, Hans, Cauchy, Augustin-Louis, in: Biographical dictionary of mathematicians. Reference biographies from the Dictionary of scientific biography, New York, Scribner's Sons, 1991, 4 v.; v. I, pp. 429-446.

Gray 1985: Gray, Jeremy J., Linear differential equations and group theory from Riemann to Poincaré, Boston-Basel, Birkhäuser, 1985 (2. ed.: 2000).

‒ 1994: Gray, Jeremy J., On the history of the Riemann mapping theorem, "Rendiconti del circolo matematico di Palermo", s. 2, 1994, suppl. 34, pp. 47-94.

Kline 1972: Kline, Morris, Mathematical thought from ancient to modern times, Oxford-New York, Oxford University Press, 1972.

Lützen 1990: Lützen, Jesper, Joseph Liouville, 1809-1882. Master of pure and applied mathematics, New York-Berlin, Springer, 1990.

Maz'ya 1998: Maz'ya, Vladimir G. - Shaposhnikova, Tatyana, Jacques Hadamard. A universal mathematician, Providence (R.I.), American Mathematical Society; London, London Mathematical Society, 1998.

Remmert 1991: Remmert, Reinhold, Theory of complex functions, translated from the 2. edition by Robert B. Burckel, New York-Berlin, Springer, 1991 (ed. orig.: Funktionentheorie, Münster, 1968).

Smithies 1997: Smithies, Frank, Cauchy and the creation of complex function theory, Cambridge, Cambridge University Press, 1997.