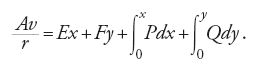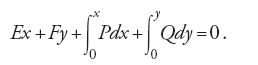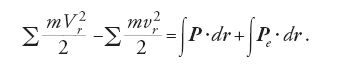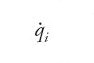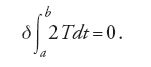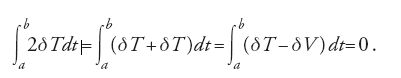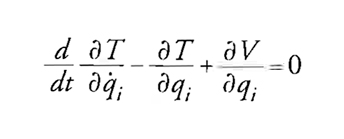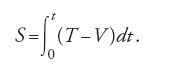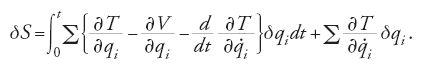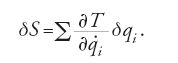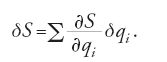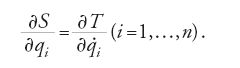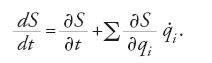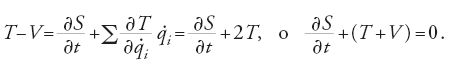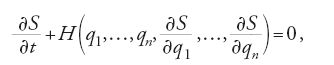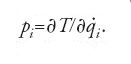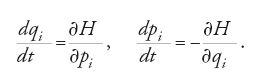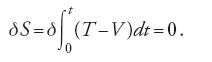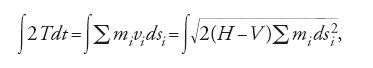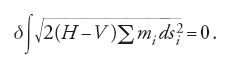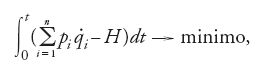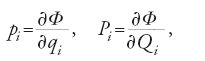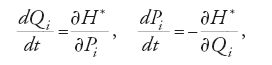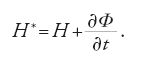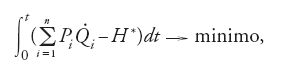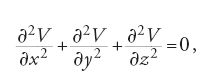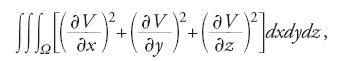L'Ottocento: fisica. Meccanica dei continui e dei sistemi discreti

L'Ottocento: fisica. Meccanica dei continui e dei sistemi discreti

Meccanica dei continui e dei sistemi discreti

Origine dei concetti di sforzo e di deformazione

La teoria matematica dell'elasticità nacque per opera di Augustin-Louis Cauchy (1789-1857) negli anni Venti dell'Ottocento, attraverso ricerche stimolate e poi completate da Claude-Louis-Marie-Henri Navier, Siméon-Denis Poisson e Augustin-Jean Fresnel. Diplomati dell'École Polytechnique, avevano tutti una formazione da ingegneri, che comprendeva però studi di matematica superiore e meccanica. Combinando elementi di calcolo, di geometria analitica e di algebra lineare, Cauchy sviluppò una teoria dei mezzi elastici che forniva una prospettiva generale allo studio dei fenomeni di elasticità, basata, tuttavia, su una concezione particolare e molto idealizzata del modo di interazione della materia.

Il principio dello sforzo è usato per analizzare il comportamento statico e dinamico di un corpo continuo quando su questo agiscono forze applicate. Vi entrano in gioco due idee distinte: la prima, logicamente indipendente dal concetto di sforzo in sé, è che un corpo, ai fini dell'analisi, si può pensare come diviso in due parti, delle quali una diviene oggetto dello studio, mentre l'effetto dell'altra su quest'ultima viene sostituito da uno specifico insieme di forze agenti sul bordo; la seconda idea è che questa separazione in due parti si può ottenere mediante un piano di divisione e, pertanto, è possibile considerare l'effetto della parte non in esame in termini di forze a unità di area, cioè di sforzi distribuiti su questo piano e che agiscono attraverso di esso.

Fu questa seconda idea a essere adottata e poi sviluppata in una teoria completa dello sforzo. Il mezzo elastico si considera continuo e in grado di sostenere forze interne su un piano arbitrariamente orientato al suo interno. Si distinguono uno sforzo normale e uno di taglio e si analizza il comportamento meccanico del corpo in termini degli sforzi che agiscono sulle facce di un prisma materiale elementare al suo interno. Mettendo in relazione questi sforzi con le deformazioni corrispondenti si ottengono le equazioni generali dell'equilibrio e del moto in un mezzo elastico isotropo.

I precedenti del XVIII secolo

Nei primi anni del Settecento si svolse una considerevole mole di lavoro per arrivare a determinare la forma che assume un corpo perfettamente flessibile sottoposto a vari carichi. L'idea di base, sviluppata dai fratelli Johann e Jakob Bernoulli e pubblicata da Jacob Hermann, fu di studiare le tensioni che agiscono su un segmento di cavo sospeso e ottenere un'equazione differenziale che descrivesse la curva risultante. Poiché il cavo era considerato inestensibile e perfettamente flessibile, non erano necessarie ipotesi sul comportamento elastico del materiale di cui era costituito.

Ipotesi sull'elasticità compaiono in due distinti e importanti problemi: il problema della rottura e quello dell'elastica. Il primo consisteva nel determinare il massimo carico che una trave di un certo materiale di dimensioni date poteva sostenere senza rompersi. Nel problema della flessione si determinava la forma assunta da una barra o da una lamina in equilibrio soggetta a forze esterne assegnate. Nel caso dell'elastica si supponeva che queste forze agissero alle estremità della barra curvandola.

Riguardo al problema della rottura, ricercatori come Gottfried Wilhelm Leibniz, Pierre Varignon e Antoine Parent ottennero risultati che si possono facilmente interpretare in termini di formule e teorie moderne. Essi formulavano l'ipotesi che la trave fosse incastrata nel muro e che la rottura avvenisse nel punto di incastro. La situazione fisica indirizzava subito l'attenzione sul piano di rottura. L'idea, allora diffusa, della trave caricata come costituita da fibre longitudinali in tensione si traduce oggi senza difficoltà in termini di tensioni che agiscono attraverso questo piano.

Per il problema della flessione elastica, invece, lo sviluppo di un'analisi che collegasse il fenomeno in questione con la struttura interna della trave fu molto più lento. In questo caso, nella situazione fisica niente permetteva di individuare un particolare piano trasversale. In nessuno dei fondamentali scritti sull'elastica di Jakob Bernoulli è mai chiaramente individuata e sviluppata l'idea centrale dello sforzo.

Il problema dell'elastica attirò l'attenzione di uno dei maggiori matematici dell'epoca, lo svizzero Leonhard Euler che nelle sue prime ricerche, non pubblicate, studiò senza successo la flessione elastica partendo da ipotesi riguardanti la struttura interna del mezzo elastico. Nelle opere pubblicate Euler abbandonerà questi tentativi; l'impostazione che seguirà lungo tutta la carriera fu enunciata nel lavoro del 1732, Solutio problematis de invenienda curva, quam format lamina utcunque elastica in singulis punctis a potentiis quibuscunque sollicitata. Lo scopo era quello di fornire una trattazione unificata dei vari risultati allora disponibili sulle curve meccaniche: catenaria, parabola, elastica, velaria, lintearia, eccetera.

Nel 'problema generale' considerato da Euler è data una lamina BMA soggetta all'estremità alla forza verticale E e orizzontale F  e si chiede di determinare la forma della curva soggetta a questo carico. Si consideri un punto qualunque M della lamina. Come momento resistente in M, Euler prende Av/r, dove v è una costante elastica, A una costante di proporzionalità e r il raggio di curvatura della curva in M. Egli deduce poi la seguente equazione differenziale per descrivere l'equilibrio statico del sistema:

Nel caso di corpi perfettamente flessibili la 'forza elastica' v è uguale a zero e la [1] si riduce a

Euler dimostra che tutte le varie forme di curve meccaniche flessibili, compresa la catenaria, si possono dedurre dalla [2]. Ritornando più avanti nel lavoro all'equazione generale [1] Euler considera esempi in cui la costante elastica v non è nulla, derivando equazioni differenziali che descrivono la curva risultante. Questa ricerca è preparatoria al famoso saggio del 1744 sulla curva elastica, nel quale è presente un'analisi completa e sistematica delle diverse soluzioni ottenute dalla [1] quando i termini integrali sono nulli.

Occorre sottolineare che in precedenza alcuni studiosi di meccanica ‒ in primis Jakob Bernoulli e Hermann ‒ avevano considerato separatamente la catenaria e l'elastica. Si otteneva l'equazione della catenaria considerando tensioni lungo un segmento del cavo sospeso, secondo un'impostazione che è più o meno quella adottata ancora oggi. L'equazione dell'elastica era ottenuta invece esaminando il comportamento elastico delle fibre che costituiscono la lamina per poter dare una stima del momento resistente in ogni punto. Basandosi sul fatto che il momento resistente di un corpo perfettamente flessibile è ovunque nullo, Euler riuscì mediante l'equazione [1] a determinare un unico metodo applicabile sia per la catenaria sia per l'elastica.

La condizione di Euler per l'equilibrio è che il momento di tutte le forze agenti sul corpo a destra di un dato punto M deve bilanciare il momento resistente in M. In sostanza egli divide la curva in due parti, studia la parte MA e analizza nel punto di confine M l'effetto su MA della seconda parte BM. Un metodo, questo, usato implicitamente da Jakob Bernoulli e da Hermann, quando uguagliavano la tensione in un dato punto di un cavo sospeso alla somma delle forze agenti sul cavo a destra (o a sinistra) di tale punto. Verso il 1750 lo stesso Euler si accorse che il principio si poteva applicare per bilanciare la forza o il momento agenti in un punto. In una memoria molto più tarda, del 1771, Genuina principia doctrinae de statu aequilibrii et motu corporum tam perfecte flexibilium quam elasticorum, egli enuncia in modo più esplicito questa condizione, integrandola con una derivazione delle equazioni differenziali generali che connettono tensione normale, tensione di taglio e momento in un punto arbitrario della curva. Con questo lavoro, e con un altro pubblicato cinque anni dopo, nel 1776, si completa la teoria di Euler dell'equilibrio statico delle curve meccaniche.

Secondo la concezione della curva elastica di Euler, il momento resistente in un dato punto è inversamente proporzionale al raggio di curvatura in quel punto. Questa è una conseguenza dell''ipotesi' enunciata all'inizio del lavoro del 1732. Euler considera due barre CB e Ba unite inizialmente in B a formare un segmento di retta. L'azione della forza AD in a fa assumere al segmento Ba la posizione BA. Euler afferma che il momento di questa forza in B è proporzionale sia alla 'forza elastica' in B sia all'angolo aBA. Un'ipotesi che, come scrive, "viene comunemente assunta e che si potrebbe probabilmente dimostrare fisicamente quando l'angolo aBA è estremamente piccolo" (Euler 1732, p. 71).

In questa concezione, oggetti fisici quali barre e travi sono idealizzati in linee unidimensionali, dotate di un certo grado di elasticità ma prive di una struttura interna passibile di ulteriore analisi, secondo una modalità che diventerà usuale nella meccanica teorica di fine Settecento. Nel 1771, una discussione della curva elastica apre un lavoro in cui Joseph-Louis Lagrange vuole dimostrare che il momento di un peso applicato P, agente all'estremità della curva, è in ogni punto uguale a P moltiplicato per la distanza (perpendicolare) del punto dalla verticale per P. Si voleva dimostrare questo risultato, noto per i corpi rigidi, anche per i corpi elastici. A questo scopo Lagrange considera una poligonale e suppone che a ogni vertice C, D, E (alla distanza λ, μ, ν) una forza, rappresentata come una specie di molla (c, d, e) eserciti un momento resistente. Egli stabilisce quindi il risultato mediante un ragionamento condotto sulla base di questo modello e lo generalizza poi a curve continue facendo crescere indefinitamente il numero dei lati della poligonale.

Passando in rassegna le opere del XVIII sec., i precedenti del concetto di sforzo si trovano in ricerche su problemi fisici concreti ‒ come la rottura di travi o l'inflessione laterale di colonne ‒ che condussero i ricercatori ad analizzare le forze interne che agiscono attraverso il piano di una sezione trasversale, sia esso il piano di rottura o quello perpendicolare all'asse maggiore della struttura. In tutti i casi l'oggetto in esame era ingegneristicamente e fisicamente definito. La situazione è illustrata in uno scritto del 1776 di Charles-Augustin Coulomb dal titolo Recherches sur la meilleure manière de fabriquer les aiguilles aimantées, sulla resistenza dei materiali e la flessione delle travi.

Quando gli scienziati cercarono di sviluppare una teoria matematica generale dell'elasticità considerarono modelli fisicamente più restrittivi. Un esempio è il problema dell'equilibrio delle curve elastiche trattato da Euler; all'inizio la sua ricerca fu condizionata dalla scelta di escludere ogni analisi delle loro proprietà nei termini del concetto di tensione interna. Egli stesso era consapevole dei limiti di questa impostazione. Nella parte iniziale dell'articolo del 1771 Euler scriveva infatti che si era ancora molto lontani da una teoria completa in grado di determinare la forma di superfici e corpi flessibili e che, per questo motivo, avrebbe limitato lo studio a "fili semplici, perfettamente flessibili o elastici, come quelli trattati finora dai geometri".

La nascita della teoria di Cauchy

Per stabilire una teoria matematica dell'elasticità ne occorreva una che unisse i punti di forza di quella di Euler ‒ carattere deduttivo, uso appropriato dell'idealizzazione e raffinatezza matematica ‒ con una sensibilità da ingegnere per il comportamento meccanico delle strutture elastiche. Un progetto di questo tipo fu effettivamente realizzato da Cauchy negli anni Venti dell'Ottocento e l'enunciazione originaria della teoria è contenuta nella famosa nota di quattro pagine pubblicata nel gennaio 1823 nel "Bulletin des sciences de la société philomatique". Hans Freudenthal osserva che "mai Cauchy aveva dato al mondo un'opera che fin dall'inizio avesse una così grande maturità" (1971, p. 145). Cauchy fu stimolato a intraprendere questa ricerca da due articoli non pubblicati di Navier e dedicati all'analisi dell'elasticità ‒ il primo sulle piastre elastiche, il secondo più generale ‒ presentati all'Académie Royale de Sciences di Parigi nell'agosto del 1820 e nel maggio del 1821. L'interesse per la teoria delle piastre era stato suscitato dagli esperimenti di Ernst Chladni (1756-1827) sulle vibrazioni delle superfici elastiche e un concorso a premi indetto dall'Académie sulle membrane elastiche aveva impegnato gli sforzi di Lagrange, Poisson e Sophie Germain.

Nelle ricerche del 1820 sulle piastre elastiche Navier parte dall'ipotesi sulla deformazione subita da un piccolo elemento cilindrico della piastra e applica il principio dei lavori virtuali di Lagrange per dedurre l'equazione differenziale alle derivate parziali ottenuta in precedenza da Lagrange e Germain. La sua memoria del 1821 è un tentativo più generale di dedurre le equazioni dell'equilibrio e del moto di un mezzo elastico. Egli utilizza un modello molecolare della struttura del mezzo nel quale suppone che la forza tra due molecole adiacenti sia proporzionale al loro spostamento relativo a seguito del carico. In alcune ricerche sulla resistenza dei materiali, culminate nel 1826 con la pubblicazione del Resumé des leçons, Navier usa questo modello che gli permette di studiare con successo per la prima volta una gamma di problemi di ingegneria, compreso quello della flessione elastica.

Il programma di ricerca di Cauchy assomigliava a quello contenuto nell'articolo di Navier del 1821. Fin dall'inizio, egli intendeva soprattutto sviluppare uno studio matematico generale delle forze interne a un corpo elastico che andasse oltre le considerazioni legate a una particolare struttura fisica. Tuttavia, invece di far uso di un'ipotesi molecolare, egli partì da un'idealizzazione di un mezzo continuo più 'euleriana' o fenomenologica. Stephen Timoshenko (1953) osserva che Cauchy applica la nozione di pressione su un piano ‒ un concetto che conosceva dall'idrodinamica ‒ supponendo che in un corpo elastico questa pressione non sia più necessariamente normale al piano su cui agisce. In tal modo l'idea di 'sforzo' (o 'tensione') entra nella teoria dell'elasticità. È opportuno peraltro osservare che Cauchy faceva uso dei termini pression e tension mentre il moderno contrainte nacque più tardi e i termini inglesi stress e strain furono introdotti nel 1858 dal fisico scozzese William Rankine.

Il successo di Navier nel determinare le equazioni corrette per una vasta classe di strutture fisiche derivava dal fatto che l'ipotesi delle forze molecolari, come da lui stesso sviluppata, si riduceva a qualcosa di molto simile a un sistema di sforzi agenti all'interno del corpo studiato. Un ulteriore stimolo per la teoria di Cauchy furono le ricerche di ottica di Fresnel sulla propagazione delle onde luminose in un etere elastico. Le proprietà di un solido elastico generico suggerite dai lavori di Fresnel fornirono a Cauchy una nuova e più astratta prospettiva per lo studio dei mezzi continui. Grazie anche a una profonda comprensione dell'algebra lineare, allora nascente, Cauchy fornì un'analisi brillante dell'insieme degli sforzi principali in un punto interno a un solido elastico. La sua teoria, delineata nella nota del 1823, fu esposta più dettagliatamente in una serie di articoli pubblicati nel 1827 e 1828.

Utilizzando metodi di algebra lineare Cauchy sviluppò anche un'analisi delle deformazioni in un corpo elastico analoga alla corrispondente analisi degli sforzi. Egli stabilì una relazione lineare tra ciascuna delle sei componenti dello sforzo in un punto del mezzo e i sei valori della deformazione nello stesso punto, applicando una forma generale della 'legge di Hooke', e dimostrò che nei mezzi isotropi il numero di costanti indipendenti in queste relazioni si riduce da trentasei a due. La questione del numero di costanti necessarie in situazioni più complicate sarà oggetto di ricerche e discussioni via via crescenti nella teoria dell'elasticità.

Nel 1828 le ricerche sull'elasticità di Cauchy entrarono in una nuova fase con l'adozione dell'ipotesi molecolare, allora prevalente, e nel corso del secolo la sua teoria degli sforzi sarà assimilata gradualmente nella sua forma originale e in tutti i suoi dettagli nella pratica scientifica e ingegneristica. L'impatto dei suoi scritti e di quelli di Navier fu immediato, come appare evidente confrontando la trattazione di Poisson della curva elastica nella prima (1811) e nella seconda (1833) edizione del Traité de mécanique. Nel 1811 Poisson adottava la concezione di Euler della curva elastica e giustificava il fatto di assimilare la lamina elastica a una curva geometrica osservando che lo spessore si supponeva costante per tutta la lunghezza. In una discussione espressa nel primo volume egli considerava la curva elastica come una poligonale a infiniti lati, in ogni vertice della quale si esercita un momento elastico, formulando l'ipotesi che il momento e l'angolo tra due segmenti successivi della poligonale fossero proporzionali. Nel 1833 Poisson scartò questo modello, sostituendolo con un'analisi in termini di sforzi agenti su piani di sezione trasversale. Egli non spiegava il perché del cambiamento; è chiaro però che la comparsa dell'analisi degli sforzi aveva reso obsoleta la concezione euleriana della curva elastica.

Analisi degli sforzi e teoria dei tensori

Nella letteratura secondaria recente si osserva la tendenza a interpretare i risultati di Cauchy in termini di concetti e notazioni della moderna analisi tensoriale. Quest'ultima disciplina ha avuto origine da quello che in geometria differenziale è noto come calcolo differenziale assoluto ed è dovuta principalmente al matematico svizzero Marcel Grossmann che la sviluppò nel corso della sua famosa collaborazione con Albert Einstein per la teoria generale della relatività. Secondo Dieter Herbert (1991) l'applicazione dei metodi tensoriali in elasticità da parte di Léon Brillouin e Paul Appel, negli anni Venti e Trenta del Novecento, dà luogo a una sostanziale discontinuità rispetto alla storia precedente della disciplina.

Anche se il calcolo tensoriale e le sue applicazioni all'elasticità si svilupparono oltre un secolo dopo Cauchy, esso viene considerato in molti scritti moderni di storia della scienza come il modo giusto di formulare i risultati originali dello stesso Cauchy. Ovviamente in opere di storia più antiche non si fa uso di notazioni o metodi tensoriali, perché non ancora sviluppati o considerati non rilevanti, e i libri di testo per non matematici, come, per esempio, il classico di Richard V. Southwell, An introduction to the theory of elasticity for engineers and physicists (1936), non ne fanno menzione.

Se i metodi tensoriali forniscono una notazione efficace essi implicano anche una più profonda comprensione concettuale del ruolo dell'invarianza nella teoria dell'elasticità. Ivor Grattan-Guinness afferma a ragione: "Ho evitato di usare il gergo moderno come 'vettore di trazione', 'quadrica di deformazione', 'superficie orientabile', eccetera. Il rispetto per la storia ci impone di prendere atto che i successori di Cauchy non avevano ancora introdotto questo linguaggio, né le relative teorie" (1990, II, p. 1009). Considerando le 'origini' del principio di sforzo, gli strumenti matematici di Cauchy erano ancora in una fase iniziale di sviluppo perché se ne possa giustificare l'interpretazione in termini di una teoria potente e moderna come il calcolo tensoriale. Saranno del resto gli sviluppi complessivi del lavoro del XIX sec. sull'elasticità matematica a fornire gli stimoli per la nascita del calcolo differenziale assoluto e dell'analisi tensoriale dal 1890 al 1920.

Trasformazione di coordinate: Coriolis

L'uso di sistemi di riferimento accelerati, cioè lo studio del moto dinamico di un insieme di corpi compiuto usando un sistema di coordinate in moto accelerato rispetto a un sistema inerziale, sembra essere stato relativamente raro nella storia della meccanica, almeno prima della metà del XIX sec.; ne sono noti, infatti, soltanto tre esempi: l'introduzione dell'accelerazione centrifuga da parte di Christiaan Huygens nel De vi centrifuga, del 1703; l'identificazione dell'accelerazione rotazionale dovuta ad Alexis-Claude Clairaut in una memoria dell'Académie Royale di Parigi del 1745; l'analisi abbastanza completa dei sistemi di riferimento accelerati compiuta da Gaspard-Gustave Coriolis negli articoli pubblicati nel "Journal de l'École Polytechnique" del 1832 e del 1835.

Coriolis faceva parte di un gruppo di ingegneri matematici francesi che negli anni Venti e Trenta dell'Ottocento aveva cominciato a studiare il rendimento delle macchine in base ai concetti di lavoro e di energia cinetica, un programma di ricerca che si può far risalire all'Essai sur les machines en général (1783) di Lazare Carnot, poi perseguito attivamente da Jean-Nicolas-Pierre Hachette (1811) e da Alexis-Thérèse Petit (1818) nei loro scritti di meccanica applicata. Nel 1829 Coriolis pubblicò un importante studio teorico sul rendimento delle macchine. Tra le altre cose, egli suggeriva di ridefinire la forza viva ‒ tradizionalmente definita ∑mv2 ‒ come (1/2) ∑mv2, una variazione che indicava il riconoscimento della priorità concettuale del lavoro nell'equazione dell'energia meccanica. Il ruolo della tradizione dell'ingegneria francese nella storica scoperta della conservazione dell'energia operata nel XIX sec. sarà messo in discussione da Thomas Kuhn nel 1962 in The structure of scientific revolutions.

La ricerca di Coriolis sui sistemi di riferimento accelerati si sviluppò a partire dal suo interesse per lo studio della conversione interna di lavoro ed energia in macchine che contengono parti accelerate. Coriolis non era interessato a uno studio puramente cinematico o matematico del moto relativo dei sistemi di coordinate e, in questo senso, il suo punto di vista era piuttosto diverso da quello che tipicamente si incontrerà poi nei libri di testo. All'inizio dell'articolo Sur le principe des forces vives dans le mouvement relatif des machines, del 1832, Coriolis richiamava l'attenzione sulle ruote idrauliche come una motivazione importante per la sua teoria. Egli considerava un sistema vincolato di corpi o una macchina che viene messa in moto e studiava il comportamento del sistema da un riferimento posto all'interno del sistema stesso. Il moto fa entrare in gioco forze assolute di vincolo che sono parzialmente bilanciate all'interno del sistema da un nuovo insieme di accelerazioni o 'forze' fittizie generate dal moto stesso. Si consideri un corpo di massa m in moto in un sistema di riferimento che sia a sua volta in moto accelerato rispetto a un sistema di coordinate fisso. Siano a_f e a_r vettori che denotano le accelerazioni di m rispettivamente nei sistemi fisso e in moto (Coriolis non usava quantità orientate, ma in questo contesto conviene adottarle per brevità). Si ha allora la seguente relazione tra ma_f e ma_r:

[3] ma_r=ma_f+P_e-ma_cor.

La forza P_e è una forza apparente, o fittizia, ed è uguale e opposta alla 'forza di trascinamento' esercitata su una massa in quiete nel riferimento in moto. L'accelerazione corrispondente a questa forza consta di tre componenti: un'accelerazione lineare di traslazione, una rotazionale e una centripeta. La quantità −a_cor è quella che sarà nota come 'accelerazione di Coriolis' ed è uguale al prodotto vettoriale −2v×ω, dove v è la velocità di m nel riferimento in moto e ω la velocità angolare di rotazione di quest'ultimo rispetto al riferimento fisso.

Nel lavoro del 1835 Coriolis identificava esplicitamente la quantità −2mv×ω riferendosi a essa come a una 'forza centrifuga composta'. Dall'equazione della forza nel riferimento assoluto si ha:

[4] maf=P+R,

dove P e R sono rispettivamente la forza applicata e la forza di vincolo che agiscono su m. Si osservi che, in generale, R comprende forze che entrano in gioco a causa del moto accelerato delle parti del sistema. Sostituendo nella [3] tale espressione di ma_f si ottiene l'equazione della forza agente su m rispetto a un sistema di coordinate posto nel sistema in moto:

[5] ma_r=P+R+P_e-ma_cor.

Coriolis osservò che l'accelerazione −a_cor è perpendicolare alla velocità relativa v di m, un fatto evidente dal punto di vista vettoriale perché a_cor=2v×ω. Quindi, se si moltiplica la [5] per vdt=dr e si integra, è chiaro che la forza −ma_cor non compie lavoro. Si suppone anche che i vincoli siano perfetti e privi di attrito, per cui anche la forza R non compie lavoro. Siano V_r e v_r i valori iniziale e finale della velocità (relativa) di m. Sommando sulle masse del sistema si ottiene l'equazione dell'energia:

Coriolis aveva dunque stabilito il fatto importante che l'equazione delle forze vive continua a valere nel riferimento accelerato se all'azione delle forze applicate si aggiunge quella delle forze P_e; queste ultime sono uguali e opposte alle forze assolute necessarie per mantenere le masse in quiete nel sistema in moto.

Nel lavoro del 1832 Coriolis era interessato in primo luogo all'applicazione dei propri risultati allo studio del moto dell'acqua nelle ruote idrauliche e in altri meccanismi rotatori. In Sur les équations du mouvement relatif des systèmes des corps del 1835 egli discute, invece, la forza centrifuga composta e deriva l'equazione generale del lavoro virtuale ('principio di d'Alembert'), che contiene questa forza per un riferimento accelerato.

Anche se la sua teoria era chiaramente originale e importante, l'influenza immediata sulla meccanica generale fu apparentemente piuttosto limitata. René Dugas (1957) afferma che il famoso esperimento di Jean-Bernard-Léon Foucault del 1851, che dimostrava il moto rotatorio del piano del pendolo, fu realizzato senza conoscere i risultati di Coriolis. L'esperimento di Foucault era però largamente qualitativo, basato sull'idea semplice che la Terra dovesse ruotare sotto il pendolo e quindi dar luogo al moto apparente osservato. Il moto del piano del pendolo è soprattutto un effetto cinematico, che non si presta molto a illustrare le idee sulla dinamica di Coriolis. Tuttavia, il risultato di Foucault divenne presto l'illustrazione consueta della teoria del moto relativo, quando questo cominciò a essere trattato nei libri di testo, come si vede dalle lezioni di meccanica generale di Henri Resnal all'École Polytechnique negli anni Settanta e Ottanta dell'Ottocento. La principale applicazione moderna delle forze di Coriolis in balistica, meteorologia e oceanografia è più tarda e non figura nelle sue ricerche originali.

Non sembra infine che Coriolis avesse un forte interesse per i fondamenti concettuali della meccanica, anche se la sua teoria ha chiare relazioni con alcuni degli argomenti che intervengono nel principio di equivalenza della teoria della relatività generale.

Il principio di Hamilton

La meccanica variazionale si sviluppò nel XVIII sec. da idee di fisica e di calcolo delle variazioni. L'aspetto che questa disciplina presentava all'epoca va considerato nel più ampio contesto delle scienze esatte del periodo, caratterizzato dal forte risalto attribuito all'individuazione e allo studio di particolari sistemi fisici. Un oggetto materiale poteva essere idealizzato in vari modi: massa puntiforme, corpo rigido, mezzo continuo deformabile, macchina, e così via. La particolare impostazione adottata era spesso influenzata dalle ipotesi che ciascuno formulava riguardo alla costituzione fisica ultima dell'Universo. La diversità dei punti di vista era notevole: si andava dalla credenza in corpuscoli perfettamente elastici (Leibniz), oppure in corpuscoli perfettamente anelastici o 'rigidi' (d'Alembert), a sistemi irriducibili di punti immersi in campi di forze (Boscovich). Tale varietà rifletteva convinzioni filosofiche e metodologiche divergenti riguardo allo studio della realtà fisica. Ciò che da un punto di vista moderno può apparire come l'analisi di un sistema speciale di tipo pratico, come quelli che s'incontrano in ingegneria meccanica, veniva invece considerato dal suo inventore come investito di significati di più ampia portata.

Si assiste infatti in questo periodo a un particolare interesse filosofico per quelle leggi fisiche che sembravano mettere in luce un aspetto teleologico e intenzionale dell'azione della Natura. Da un punto di vista scientifico, tuttavia, l'importanza della meccanica variazionale consiste non tanto nell'aver ampliato la nostra comprensione dei fenomeni fisici quanto piuttosto nell'aver proposto nuovi metodi e tecniche, nonché di aver fornito una formulazione matematica per lo studio dei sistemi dinamici. Lo sviluppo della meccanica variazionale fu soprattutto opera di Leonhard Euler e Joseph-Louis Lagrange. Nel 1744 Euler pubblicava un trattato di rilievo assoluto sul calcolo delle variazioni, la Methodus inveniendi lineas curvas, seguito otto anni più tardi da un lavoro di dinamica variazionale. Le scoperte di Lagrange sono contenute in uno scritto del 1762 sul principio di minima azione e nella Méchanique analitique del 1788.

Dal punto di vista della fisica del XIX sec. gli scritti di Lagrange sono quelli che presentano il massimo interesse. Nel suo primo lavoro di matematica egli introduce il procedimento δ (di variazione) nel calcolo delle variazioni. In una lettera del 1755 a Euler, Lagrange annuncia di essere finalmente riuscito a ottenere un metodo generale per risolvere i problemi presentati nella Methodus inveniendi. Il suo algoritmo δ permette la derivazione sistematica delle equazioni variazionali e facilita, al contempo, la trattazione di problemi nei quali sono presenti estremi variabili. Il metodo venne adottato da Euler come pure da tutti i ricercatori che seguirono e consentì di rifondare la disciplina su nuove basi.

Sebbene apparentemente introdotto come un mezzo per confrontare curve nello spazio, il procedimento di variazione δ fu nondimeno presentato in modo molto formale. Il simbolo δ ha proprietà analoghe a quelle dell'usuale simbolo d del calcolo differenziale. Così δ(x+y)=δx+δy e δ(xy)==xδy+yδx. Inoltre, d e δ sono permutabili (dδ=δd), come lo sono δ e il simbolo di integrazione ∫. Lagrange applicò nel 1762 questo procedimento alla dinamica, cominciando con il principio di minima azione, nella formulazione che Euler ne aveva dato nove anni prima. Egli presenta dapprima la propria analisi nel caso di una sola particella sulla quale agiscono forze centrali, per poi proseguire con un generico sistema dinamico vincolato.

Il procedimento si può riassumere come segue: sia il moto descritto in termini delle coordinate q_i, i=1,2,…,n e delle loro derivate

in funzione del tempo, e sia 2T la forza viva del sistema, cioè 2T=∑mv2. Il principio di minima azione viene espresso nella forma seguente:

Si consideri ora quella che era nota come equazione delle forze vive (in termini moderni, energia meccanica):

[8] T+V=h,

dove V denota il potenziale e h è una costante. Applicando l'algoritmo si ottiene

[9] δT+δV=0.

Scambiando δ e ∫ nella [7], tenuto inoltre conto della [9] si ha:

Il resto consiste nell'ottenere le equazioni del moto dalla [10] usando tecniche del calcolo delle variazioni. Lagrange determina le equazioni variazionali standard nella forma

e nella memoria applica questo procedimento a una serie di esempi via via più complicati, usando coordinate q_i di vari sistemi di riferimento.

Apparentemente Lagrange non sembrava molto interessato a una comprensione delle basi fisiche del principio di minima azione. Interpretato come una legge strettamente variazionale, il suo procedimento è suscettibile di critica: esso infatti suppone che sia il tempo sia l'energia totale restino invariati nel processo variazionale; un requisito troppo restrittivo dal punto di vista fisico. Da un punto di vista logico il metodo si riduce all'affermazione che le equazioni lagrangiane [11] seguano dalla [10] e in questa forma il principio coincide con quello che oggi è noto come 'principio di Hamilton'.

In ogni caso, dopo il 1762 Lagrange rigetta come punto di partenza per la meccanica i principî variazionali integrali. Negli scritti del 1764 e del 1780, come pure nella Méchanique analitique del 1788, l'assioma fondamentale della sua meccanica è una generalizzazione dinamica del principio dei lavori virtuali. Nella Méchanique analitique Lagrange è molto critico nei confronti di nozioni quali il principio di minima azione e, più in generale, riguardo ai principî variazionali integrali, soprattutto per quanto di vago e di metafisico vi vedeva associato.

Il lavoro di Hamilton del 1835

Il matematico irlandese William R. Hamilton (1805-1865) ha posto le basi di una nuova teoria dinamica in due articoli pubblicati nelle "Philosophical Transactions" della Royal Society di Londra: On a general method employed in dynamics, del 1834, e Second essay on a general method in dynamics, del 1835. Dopo gli studi al Trinity College di Dublino, Hamilton era diventato astronomo reale d'Irlanda e direttore dell'Osservatorio di Dunsink. Oltre che per i suoi lavori sulla dinamica viene oggi ricordato per aver creato una nuova struttura algebrica: i quaternioni. Alcune delle idee di fisica provengono dai suoi primi lavori di ottica; in dinamica esse furono motivate dallo studio di problemi di perturbazione del moto dei pianeti.

Le ricerche di Hamilton sulla dinamica si svolsero nell'ambito della meccanica analitica, così come era stata fondata da Lagrange. Gli elementi principali della sua nuova teoria si trovano alla fine dell'articolo del 1834 e, più compiutamente, in quello del 1835. La prima e più importante innovazione consistette nel legare le tradizionali equazioni differenziali ordinarie del moto a un'equazione alle derivate parziali nella quale interviene quella che egli chiama 'funzione principale'. L'equazione differenziale alle derivate parziali che ne risulta sarà nota in seguito nella dinamica come 'equazione di Hamilton-Jacobi'.

L'idea matematica che sta alla base della sua formalizzazione ‒ ma che Hamilton non mise mai del tutto chiaramente in luce e della quale probabilmente non fu mai consapevole ‒ è di considerare un integrale definito in un modo particolare, vale a dire come una quantità calcolata lungo una delle curve soluzione delle equazioni differenziali dinamiche associate. L'integrale che ne risulta si può considerare come una funzione del tempo t e dei valori estremi delle coordinate. Prendendo la variazione di questo integrale, si ottiene un'espressione priva della componente integrale, nella quale compaiono soltanto quantità che vengono calcolate nei punti estremi (un'idea che sarebbe stata poi sviluppata nel calcolo delle variazioni dando luogo a una potente nozione nota come 'integrale di campo'). Sia T−V, la lagrangiana del problema, la funzione integranda in questione. La funzione principale S è allora definita come

S va considerata funzione dei valori iniziale e finale di t e delle coordinate generalizzate q1, q2,…,q_n. In quel che segue limiteremo per semplicità le nostre considerazioni al caso in cui i valori iniziali sono fissati, per cui interverranno nella S solo i valori finali delle q_i. Prendendo la variazione di S si ottiene con un procedimento standard del calcolo delle variazioni

Poiché S viene calcolata lungo una curva soluzione delle equazioni dinamiche, il termine integrale della [13] si riduce a zero (per la [11]) e si ottiene l'equazione:

Poiché S è una funzione delle q_i si ha anche l'identità:

Confrontando i coefficienti delle δq_i nelle [14] e [15] si arriva alle uguaglianze:

Derivando S rispetto al tempo si ha:

Dalla [12] risulta evidente che dS/dt=T−V. Usando questa relazione e la [16] si ottiene dalla [17]:

Grazie alla [16] è possibile esprimere le

in termini dei ∂S/∂q_i. Dalla [18] si ottiene allora l'equazione differenziale alle derivate parziali di Hamilton-Jacobi del problema:

dove H=T+V, l'energia totale, è l'hamiltoniana del sistema. La [19] è un'equazione differenziale non lineare alle derivate parziali del primo ordine nelle variabili q1,q2,…,q_n, t e S, in cui S non appare esplicitamente.

L'altra idea fondamentale di Hamilton fu di mostrare come l'equazione del moto si possa esprimere in una forma 'canonica' alternativa. A partire da un'idea che aveva forse trovato negli scritti di Poisson, Hamilton uguaglia la derivata parziale di T rispetto a

a una nuova variabile p_i, ponendo

Egli dimostra che le n equazioni lagrangiane del secondo ordine [11] sono equivalenti alle 2n equazioni del primo ordine:

Le [20] sarebbero state chiamate 'equazioni canoniche' dal matematico di Königsberg Carl Gustav Jacob Jacobi, contemporaneo di Hamilton.

Ottenute le [20] Hamilton osservò che, se i punti estremi sono fissi, allora dalla [14] segue δS=0 e quindi

La [21] esprime il 'principio di Hamilton', secondo il quale la variazione dell'integrale della lagrangiana T−V è uguale a zero. Fu Jacobi a richiamare l'attenzione sul principio di Hamilton e ad assegnargli questo nome, sottolineandone l'importanza come legge fondamentale della meccanica variazionale. I contributi di Jacobi sono contenuti in una serie di articoli pubblicati alla fine degli anni Trenta e Quaranta del secolo e nelle Vorlesungen über Dynamik (Lezioni di dinamica), pubblicate postume nel 1866.

Nelle Vorlesungen Jacobi formula un principio variazionale integrale alternativo, che generalizza una legge proposta da Euler in un'appendice della Methodus inveniendi. Usando l'equazione della forza viva Jacobi esprime l'azione integrale nella forma

in cui la variabile tempo e le velocità sono state eliminate dall'integrando variazionale. Il principio di minima azione nella forma di Jacobi afferma che:

Qui si suppone, a differenza del principio di Hamilton, che nel procedimento variazionale l'energia totale non vari. Se si considera questo un principio fisico, allora le curve di confronto si ottengono introducendo forze di vincolo senza attrito e con un tempo di transito che è differente lungo le diverse curve. Nel principio di Hamilton invece le curve di confronto, viste come traiettorie fisicamente possibili, si ottengono introducendo qualunque ulteriore forza applicata, necessaria per assicurare l'invarianza del tempo di transito lungo il cammino di confronto. Anche se il principio di Hamilton conduce a una descrizione matematica corretta del moto, la classe delle curve di confronto non è però specificata in modo naturale da un punto di vista fisico; al principio sembra mancare quel carattere fenomenologico evidente che ci si aspetterebbe da una legge fisica fondamentale.

Storicamente, le equazioni del moto nella forma lagrangiana furono scoperte come equazioni variazionali che seguono da un principio integrale variazionale opportunamente formulato. È quanto fa Lagrange nell'Essai d'une nouvelle méthode pour déterminer les maxima et les minima des formules intégrales indéfinies del 1762; il calcolo delle variazioni forniva il contesto matematico per le scoperte sia della meccanica lagrangiana sia di quella hamiltoniana.

Va tuttavia sottolineato che nella Méchanique analitique Lagrange mette da parte il principio di minima azione, prendendo come postulato fondamentale il principio dei lavori virtuali. Hamilton non derivava le equazioni del moto ‒ in forma lagrangiana o canonica ‒ dal principio che egli stesso aveva formulato o da altro principio variazionale integrale. Egli deduceva invece tali equazioni da principî basati fondamentalmente su ipotesi riguardanti l'equivalenza tra forza e accelerazione; questa impostazione metteva in luce una profonda resistenza, apparentemente inconscia, a fare di un principio variazionale integrale il punto di partenza a priori di ogni ricerca dinamica.

Il maggiore risultato di Hamilton non fu il principio variazionale che da lui prende il nome bensì l'idea di collegare lo studio del sistema a una singola funzione ‒ definita dalla [12] ‒ data in termini di un'equazione differenziale alle derivate parziali. Lo sviluppo che ne seguì, e che aprì ampie prospettive teoriche, si ebbe senza supporre la validità di alcun particolare principio variazionale integrale. Sebbene scoperti storicamente nel quadro della meccanica variazionale, gli usuali vantaggi derivanti da una formulazione lagrangiana o hamiltoniana ‒ flessibilità nella scelta delle coordinate, uso di quantità scalari e invarianza delle equazioni ‒ apparivano logicamente indipendenti dall'adozione di principî variazionali integrali.

Applicazioni dei principî variazionali integrali

In tutto il XIX sec. si fece frequentemente uso di metodi basati sul principio dei lavori virtuali ‒ nati nella Méchanique analitique ‒ al fine di studiare il comportamento di vari problemi meccanici. Il principio rilevante era il 'principio di d'Alembert', che afferma l'uguaglianza tra il lavoro compiuto dalle forze inerziali e da quelle applicate in un piccolo spostamento virtuale del sistema. Sia Navier sia Coriolis si avvalsero di questa impostazione nelle ricerche che abbiamo precedentemente descritto. Anche se comportano formalmente l'utilizzazione di tecniche variazionali, questi metodi non dipendono da ipotesi iniziali sulla minimizzazione di una quantità integrale e quindi non sono completamente variazionali.

Malgrado il principio di Hamilton e altri principî variazionali integrali non fossero considerati, da chi li aveva stabiliti, il punto di partenza della teoria dinamica, essi restavano comunque strumenti importanti in diverse aree della meccanica matematica. Benché rigore e chiarezza di idee siano spesso mancati nelle discussioni relative alla fisica variazionale, alcuni esempi mostrano inequivocabilmente l'importanza del ruolo assunto dai principî integrali.

Uno degli obiettivi principali in un problema di dinamica è quello di trovare un opportuno insieme di coordinate che permetta l'integrazione delle equazioni del moto. Il risultato principale riguardo a questo problema è un teorema di trasformazione enunciato per la prima volta (ma non dimostrato) da Jacobi già nel 1837 e largamente utilizzato da matematici come Jules-Henri Poincaré alla fine del XIX secolo. Tenendo presente che la lagrangiana si può esprimere in termini delle n coordinate indipendenti q_i e degli n momenti coniugati p_i come

applicando il principio di Hamilton si ottiene il problema variazionale:

dove le coordinate q_i e i momenti p_i vanno considerati come 2n funzioni indipendenti di t. Le equazioni canoniche [20] sono semplicemente le equazioni variazionali di Euler per questo problema. Supponiamo ora che q_i e p_i siano legati a nuove variabili Q_i e P_i da equazioni del tipo

dove la 'funzione generatrice' Φ è definita da:

[27] Φ=Φ(t,q₁,…,q_n, Q₁,…,Q_n).

Il risultato fondamentale di Jacobi afferma che Q_i e P_i soddisfano equazioni canoniche della forma

dove la nuova hamiltoniana H* è:

La dimostrazione di questo risultato si basa sull'osservazione che le [28] sono le equazioni variazionali di Euler per il problema:

nel quale Q_i e P_i sono 2n funzioni indipendenti di t. Affinché la [25] definisca lo stesso problema variazionale della [30] occorre ‒ come si vede facilmente con considerazioni di calcolo delle variazioni ‒ che le funzioni integrande delle [25] e [30] differiscano per un differenziale esatto della forma dΦ, una condizione assicurata dal sussistere delle [26].

Il teorema di trasformazione di Jacobi è un risultato importante nella teoria delle perturbazioni in meccanica celeste e nella matematica delle moderne teorie quantistiche. Di questo risultato va sottolineato il carattere fondamentale, l'utilità nelle teorie fisiche moderne e il ruolo essenziale che gioca il principio di Hamilton nella sua dimostrazione.

Un altro esempio è dato dall'uso più generale di principî variazionali integrali per stabilire l'esistenza di soluzioni relative a problemi di fisica matematica. In questi problemi si considera generalmente una funzione definita su un mezzo continuo o su un corpo esteso, della quale occorre dimostrare che soddisfa un'equazione differenziale alle derivate parziali e che assume un assegnato valore sulla frontiera. Il problema viene riformulato come un problema di calcolo delle variazioni che comporta la minimizzazione di una certa quantità, scelta in modo tale che l'equazione variazionale di Euler concida con la data equazione differenziale alle derivate parziali. Se il problema variazionale ha soluzione, anche il problema originario ha soluzione. Ragionano così Carl Friedrich Gauss (1839), William Thomson (1847) e Peter Gustav Lejeune Dirichlet (1856); l'idea di base, che si utilizza anche in campi della matematica pura come l'analisi complessa, è nota oggi come 'principio di Dirichlet'.

Le applicazioni che il principio di Dirichlet ebbe nel corso del tempo illustrano come i metodi variazionali con integrali multipli furono usati nello studio di mezzi continui, potenziali gravitazionali e campi elettromagnetici. In alcuni problemi di elettrostatica o di teoria del potenziale si deve dimostrare che la soluzione V=V(x,y,z) soddisfa l'equazione di Laplace,

in una certa regione Ω e assume un assegnato valore V0 sulla frontiera ∂Ω. Questo problema viene riformulato come un problema di minimizzazione dell'integrale:

dove si richiede che V=V0 su ∂Ω. L'equazione variazionale di Euler per questo problema è semplicemente la [31], come si può facilmente verificare. Se si riesce a stabilire, per ragioni fisiche o matematiche, l'esistenza di una soluzione funzionale del problema variazionale, allora la funzione trovata è la soluzione del problema originario.

Una terza applicazione dei principî variazionali integrali si ebbe nelle parti più astratte della meccanica matematica, là dove si esplorano i legami tra geometria differenziale e dinamica. Anche se questo sviluppo appartiene più alla matematica che alla fisica, esso può avere avuto un ruolo ‒ almeno come sfondo ‒ nella nascita della relatività generale e della cosmologia nel periodo 1910-1925. Il risultato fondamentale qui è il principio variazionale di Jacobi [23], che Dugas (1957) definisce "una geometrizzazione del principio di minima azione".

L'idea è di mettere in relazione la dinamica con la teoria delle geodetiche, per cui il moto del sistema tra due configurazioni viene visto come quello che minimizza la 'distanza' definita dall'integrale nella [23]. Nel caso di una singola particella che si muove su una superficie con potenziale costante (cioè senza forze esterne), nella [23] si ha V=costante e il principio variazionale afferma semplicemente che la traiettoria seguita dalla particella è il cammino più breve ∫^b_ads tra gli estremi. Jacobi usa questa idea e il formalismo delle equazioni di Hamilton-Jacobi nello studio del 1838 delle geodetiche sulla superficie di un ellissoide. Questa linea di pensiero sarà alla base di una serie di ricerche matematiche sempre più astratte, la più notevole delle quali fu lo studio di Rudolf Lipschitz del 1872 sulla geometria differenziale della dinamica non euclidea.

Studi

Belhoste 1991: Belhoste, Bruno, Augustin-Louis Cauchy. A biography, translated by Frank Ragland, New York-Berlin, Springer, 1991 (ed. orig.: Cauchy 1789-1857. Un mathématicien légitimiste au XIXème siècle, Paris, Belin, 1988).

Bertoloni Meli 1993: Bertoloni Meli, Domenico, The emergence of reference frames and the transformation of mechanics in the Enlightenment, "Historical studies in the physical and biological sciences", 23, 1993, pp. 301-335.

Bucciarelli 1980: Bucciarelli, Louis L. - Dworsky, Nancy, Sophie Germain. An essay in the theory of elasticity, Dordrecht-Boston, Reidel, 1980.

Costabel 1971: Costabel, Pierre, Gaspard Gustave de Coriolis, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner's Sons, 1970-1990, 18 v.; v. III, 1971, pp. 416-419.

Dahan-Dalmédico 1992: Dahan-Dalmédico, Amy, Mathématisations. Augustin-Louis Cauchy et l'École française, Argenteuil, Éditions du Choix; Paris, Blanchard, 1992.

Dugas 1957: Dugas, René, A history of mechanics, translated by J.R. Maddox, London, Routledge & Kegan, 1957 (ed. orig.: Histoire de la méchanique, Neuchâtel, Éditions du Griffon, 1950).

Fraser 1991: Fraser, Craig G., Mathematical technique and physical conception in Euler's investigation of the elastica, "Centaurus", 34, 1991, pp. 211-246.

‒ 1995: Fraser, Craig G., The concept of elastic stress in eighteenth-century mechanics. Some examples from Euler, in: Hamiltonian dynamical systems. History, theory and applications, edited by Scott H. Dumas, Kenneth R. Meyer and Dieter S. Schmidt, New York, Springer, 1995, pp. 1-14.

Freudenthal 1971: Freudenthal, Hans, Augustin-Louis Cauchy, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner's Son, 1970-1990, 18 v.; v. III, 1971, pp. 131-148.

Grattan-Guinness 1984: Grattan-Guinness, Ivor, Work for the workers. Advances in engineering mechanics and instruction in France, 1800-1830, "Annals of science", 41, 1984, pp. 1-33.

‒ 1990: Grattan-Guinness, Ivor, Convolutions in French mathematics, 1800-1840, Basel, Birkhäuser, 1990, 3 v.

Hankins 1980: Hankins, Thomas L., Sir William Rowan Hamilton, Baltimore, Johns Hopkins University Press, 1980.

Hawkins 1975: Hawkins, Thomas W., Cauchy and the spectral theory of matrices, "Historia mathematica", 2, 1975, pp. 1-126.

Herbert 1991: Herbert, Dieter, Die Enstehung des Tensorkalküls: von den Anfängen in der Elastizitätstheorie bis zur Verwendung in der Baustatik, Stuttgart, Steiner, 1991.

Heyman 1972: Heyman, Jacques, Coulomb's memoir on statics. An essay in the history of civil engineering, Cambridge (Mass.), Cambridge University Press, 1972.

Kuhn 1969: Kuhn, Thomas S., Energy conservation as an example of simultaneous discovery, in: Critical problems in the history of science, edited by Marshall Clagett, Madison, University of Wisconsin Press, 1969, pp. 321-356 (1. ed.: 1959).

Lützen 1995: Lützen, Jesper, Interaction between mechanics and differential geometry in the 19th century, "Archive for history of exact sciences", 49, 1995, pp. 1-72.

Monna 1975: Monna, Antonie F., Dirichlet's principle. A mathematical comedy of errors and its influence on the development of analysis, Utrecht, Oosthoek, Scheltema & Holkema, 1975.

Southwell 1936: Southwell, Richard V., An introduction to the theory of elasticity for engineers and physicists, Oxford, Clarendon, 1936 (2. ed.: Oxford, Oxford University Press, 1941).

Timoshenko 1953: Timoshenko, Stephen P., History of strength of materials with a brief account of the history of theory of elasticity and theory of structures, New York, McGraw Hill, 1953.

Truesdell 1960: Truesdell, Clifford, The rational mechanics of flexible or elastic bodies, 1638-1788. Introduction to Leonhardi Euleri opera omnia, vol X et XI seriei secundae, in: Euler, Leonhard, Opera omnia, ser. II, v. 11/II, 1960.

‒ 1968: Truesdell, Clifford A., The creation and unfolding of the concept of stress, in: Truesdell, Clifford A., Essays in the history of mechanics, New York-Berlin, Springer, 1968, pp. 184-238.