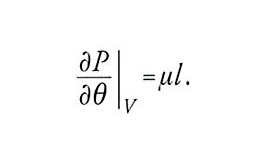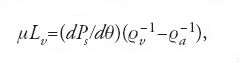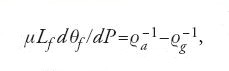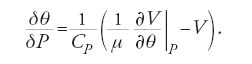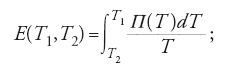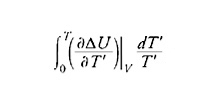L'Ottocento: fisica. La termodinamica

L'Ottocento: fisica. La termodinamica

La termodinamica

Termodinamica è il nome dato da William Thomson (futuro lord Kelvin) nel 1854 alla nuova teoria meccanica del calore, fondata da lui e da Rudolf Clausius negli anni tra il 1850 e il 1851. Essi giunsero a formularla modificando quella delle macchine termiche elaborata da Sadi Carnot, in modo da soddisfare il principio enunciato da James P. Joule sull'equivalenza tra calore e lavoro meccanico.

I due fondamenti di questa nuova scienza ponevano vincoli, come subito si resero conto Thomson e Clausius, alla possibile forma di ogni legge macroscopica riguardante gli effetti termici. Secondo la loro visione, l'universalità della termodinamica dipendeva dalla possibilità di ricondurre tutta la fisica alla meccanica; allo stesso tempo, però, essi si sforzarono di separare la termodinamica macroscopica dai suoi fondamenti ultimi cinetico-molecolari. Coerentemente con questo atteggiamento e con la stabilizzata autonomia e solidità attuale della termodinamica, la storia di tale scienza viene trattata in questa sede in modo indipendente dalla storia della meccanica statistica.

Le origini storiche della termodinamica dipendono fondamentalmente dall'adeguamento della meccanica alle necessità della teoria delle macchine, attuato agli inizi del XIX secolo. A partire almeno da Galilei, la capacità delle macchine di compiere lavoro era stata misurata dall'elevazione di un peso moltiplicata per il valore di quest'ultimo. Tale metodo, come discusso da Gottfried Wilhelm Leibniz alla fine del XVII sec., insieme alla legge di Galilei della caduta dei gravi, faceva della 'forza viva' (la massa moltiplicata per il quadrato della velocità) una misura del movimento di un corpo più importante della quantità di moto di Newton o di Descartes. Modificando il concetto teologico di conservazione del moto di Descartes, e generalizzando le affermazioni di Christiaan Huygens sugli urti elastici e sulle oscillazioni del pendolo, Leibniz giunse a ipotizzare che nell'Universo la quantità totale di forza viva si conservasse.

Nel XVIII sec., il successo della fisica newtoniana e lo sviluppo della meccanica razionale francese impedirono la diffusione del concetto leibniziano di 'forza viva'. Due notevoli eccezioni furono rappresentate dagli studi sulla ruota idraulica condotti dall'ingegnere John Smeaton in Inghilterra e da Jean-Charles Borda in Francia. Seguendo Borda, Lazare Carnot sviluppò nell'Essai sur les machines en général (1783) e nei successivi Principes fondamentaux de l'équilibre et du mouvement (1803) una teoria generale delle macchine, in cui i concetti di 'forza viva' e di 'lavoro' (moment d'activité) giocavano un ruolo centrale. Egli dimostrò che, per una macchina posta in attività in modo continuo, il lavoro totale delle forze agenti uguaglia una variazione della forza viva pari alla metà di questa. Il ruolo della macchina, quindi, consiste nel convertire il lavoro delle forze motrici in lavoro contro le forze resistenti, con una perdita corrispondente al lavoro delle forze interne di attrito. Durante qualsiasi discontinuità nel funzionamento della macchina c'è un'ulteriore perdita dipendente dalla variazione del quadrato della velocità. L. Carnot sottolineò che la quantità meccanica rilevante dal punto di vista economico era il lavoro. Al fine di preservarlo nella maggior misura possibile, si rendeva necessario che il movimento delle macchine fosse quanto più possibile simile a un movimento reversibile.

Le idee di L. Carnot erano formulate nel quadro di una nuova meccanica, la cui astrattezza rappresentava un deterrente per molti lettori; negli anni Dieci e Venti del XIX sec. esse furono rese popolari da una nuova generazione di ingegneri di impostazione matematica, formatisi all'école Polytechnique. Claude-Louis-Marie-Henri Navier ridefinì una macchina in base alla sua funzione di trasmettere lavoro; Gaspard-Gustave Coriolis introdusse il termine 'lavoro' e ridefinì la forza viva come il lavoro che un corpo in movimento è in grado di produrre; Jean-Victor Poncelet, infine, inserì il concetto di 'lavoro' al centro dei suoi corsi di meccanica. Così riformulata, la meccanica divenne più direttamente applicabile alle macchine e più accessibile a chi aveva scarse basi matematiche. Negli anni tra il 1830 e il 1850 la maggior parte degli autori tedeschi e inglesi che si occupavano di ingegneria meccanica adottò il nuovo approccio francese e questo cambiamento cominciò a riflettersi anche nei trattati sui fondamenti della meccanica.

Nella teoria delle macchine di L.Carnot, come nella dinamica di d'Alembert e nella meccanica analitica di Lagrange, le parti del sistema erano idealizzate come corpi assolutamente rigidi, le cui collisioni comportavano alla fine una distruzione del moto. Per esempio, una sfera rigida, urtando perpendicolarmente una parete, si arrestava istantaneamente. Processi come questi erano alla base della dinamica così come l'avevano concepita d'Alembert e Lagrange. Analogamente, l'attrito era considerato come una distruzione parziale del moto e, di conseguenza, parte del lavoro erogato da una macchina reale veniva definitivamente perso. Nell'Universo di L. Carnot, la forza viva totale disponibile diminuiva nel tempo, analogamente a quanto avevano fermamente creduto Newton e i suoi seguaci inglesi, per i quali si aveva distruzione del moto durante gli urti tra atomi, intesi, questi ultimi, come sferette infinitamente rigide e anelastiche.

Leibniz, l'ideatore della forza viva, aveva una visione opposta, secondo la quale il moto totale dell'Universo, misurato dalla sua forza viva, era una costante, sotto l'esclusivo controllo di Dio. L'apparente distruzione di forza viva era in effetti una ridistribuzione del moto visibile tra le componenti piccole e invisibili del sistema. In maniera analoga Smeaton credeva che la perdita di potenza in una turbina idraulica in rotazione fosse compensata da un 'cambiamento di figura' dell'acqua incidente. Nei decenni intercorsi tra il 1820 e il 1840 Navier, Coriolis e Poncelet rinunciarono alla visione idealizzata di corpo rigido, e tornarono a quella leibniziana. Seguendo Pierre-Simon de Laplace e il suo discepolo Siméon-Denis Poisson, essi sostituirono le idealizzazioni della precedente meccanica razionale con una 'meccanica fisica' che teneva conto dell'elasticità, della plasticità e di altre caratteristiche fisiche dei corpi.

Per questo essi ritenevano che tutta la materia (ponderabile e imponderabile) fosse composta di molecole che interagivano esclusivamente attraverso forze centrali. In questo quadro le perdite apparenti di lavoro corrispondevano davvero a una 'dissipazione'(per usare un termine di Poncelet) in movimenti o riorganizzazioni molecolari.

In uno scritto del 1830, mai pubblicato, l'ingegnere del genio civile Adhémar-Jean-Claude Barré de Saint-Venant formalizzò questo punto di vista, ponendolo a fondamento di una nuova legge di conservazione della Natura. Come era ben noto tanto a Leonhard Euler quanto a Lagrange, la quantità definita come la metà della forza viva totale di un sistema meccanico governato da forze centrali può aumentare soltanto a spese della diminuzione del potenziale totale delle forze; Saint-Venant applicò questo teorema all'intero Universo e lo riformulò in termini di conservazione di un 'capitale dinamico', costituito da una parte 'manifesta' e da una 'latente', tenendo presente, naturalmente, il legame tra il potenziale, la forza viva e il lavoro compiuto dalle macchine, e intendendo anche dare giustificazione della grandiosa concezione della conservazione del moto di Descartes e Leibniz.

In alcuni casi, le compensazioni immaginate da Poncelet e Saint-Venant per l'apparente perdita di moto corrispondevano a effetti visibili, come il logoramento di parti meccaniche, le vibrazioni indesiderate o l'agitazione indotta nell'acqua. In altri casi, la compensazione sembrava limitarsi all'invisibile moto molecolare; che questi effetti potessero essere misurati dal calore prodotto non fu considerato dagli ingegneri francesi, tutti convinti della conservazione del fluido calorico. I concetti di conservazione e di dissipazione di Poncelet e Saint-Venant mancavano così di supporto sperimentale e rimanevano convinzioni basate su una rappresentazione plausibile dell'Universo.

La potenza motrice del calore

I sostenitori francesi del concetto di 'lavoro' si occupavano solo di macchine meccaniche. I motori a vapore erano meno diffusi in Francia rispetto all'Inghilterra, e divennero importanti soltanto in seguito allo sviluppo del trasporto ferroviario. Tuttavia, in Francia, erano stati effettuati alcuni studi sulla produzione di potenza per mezzo del vapore, compreso un libro poco conosciuto di Sadi Carnot, figlio di Lazare. Prima di prendere in considerazione questo lavoro fondamentale, si devono però ricordare alcune nozioni preliminari sul calore, sui gas e sulle macchine a vapore.

Nel 1800 la termometria era ormai una scienza ben consolidata, con applicazioni in diversi campi, comprese la medicina, la meteorologia e la fisica. La scelta della scala termometrica e del fluido utilizzato variava: la temperatura, come osservò in seguito Ernst Mach (1838-1916), non era altro che un'etichetta convenzionale dei diversi gradi di calore. I tentativi compiuti per fornirne una definizione assoluta, come per esempio quello realizzato intorno al 1770 da Jean-André Deluc (1727-1817) attraverso il metodo del mescolamento, non erano esenti da critiche. Dopo gli esperimenti accurati di Joseph-Louis Gay-Lussac nel 1802, a dimostrazione che tutti i gas si espandono in ugual modo per una data variazione della temperatura, la migliore proposta consisteva nel definire la temperatura θ in modo tale che la pressione P e il volume V di una massa unitaria di gas fossero legati a essa dalla relazione PV=Rθ, con R costante (che combina la legge di Boyle e la legge di Gay-Lussac). Soltanto intorno al 1840, grazie alle sofisticate misure di Heinrich Gustav Magnus a Berlino e di Henri-Victor Regnault a Parigi, fu chiaro che a densità elevate si avevano deviazioni importanti da questa legge.

Negli anni Sessanta del Settecento il filosofo naturale scozzese Joseph Black (1728-1799) definì la capacità termica di corpi diversi confrontando i tempi necessari a innalzarne la temperatura di un dato intervallo e in modo simile definì il calore latente di evaporazione e quello di fusione. Sebbene lo stesso Black rifuggisse dal formulare ipotesi sulla natura del calore, sia i suoi discepoli scozzesi sia il chimico francese Antoine-Laurent Lavoisier (1743-1794) introdussero il concetto di 'fluido calorico' ed elaborarono teorie sul tipo di interazione esistente tra il calorico e le molecole di materia. Insieme a Laplace, inoltre, Lavoisier sviluppò alcune tecniche calorimetriche accurate, mentre all'inizio del XIX sec. Laplace incluse il fluido calorico autorepulsivo nella propria teoria matematica della materia. Diversi suoi colleghi francesi svilupparono la calorimetria dei gas, sperando così di poter discriminare tra le diverse teorie sul calorico. Nel 1820 la calorimetria scozzese, la fisica di Laplace e l'analogia tra il calore radiante e la luce avevano ormai soppiantato quasi completamente la vecchia idea newtoniana del calore come modalità di movimento.

Lo sviluppo della produzione di potenza dal vapore ebbe luogo nell'Inghilterra del XVIII sec. indipendentemente da qualsiasi teoria sul calore. Il principale incentivo era rappresentato dalla possibilità di facilitare il lavoro nelle miniere di carbone, dalle quali l'industria inglese dipendeva fortemente. Il primo motore a vapore di larga utilizzazione, inventato da Thomas Newcomen (1663-1729) nel 1712, era costituito da un sistema pistone-cilindro in cui potevano entrare alternativamente il vapore proveniente da una caldaia oppure acqua fredda; quando l'acqua fredda provocava la condensazione del vapore, nel cilindro si produceva un vuoto, e la pressione atmosferica esterna spingeva in giù il pistone. Nel prosieguo dello stesso secolo, il fabbricante di strumenti di Glasgow James Watt (1736-1819) perfezionò notevolmente il motore di Newcomen; provando a minimizzare il calore disperso durante la fase di condensazione, egli concepì l'idea di due cilindri separati, uno per l'azione del vapore sul pistone, l'altro per la condensazione del vapore. Per evitare la perdita di lavoro dovuta al flusso di vapore tra i due cilindri, fece in modo che esso potesse espandersi nel cilindro caldo prima di aprire la comunicazione con il cilindro di condensazione. Nel Traité de physique del 1816, un testo all'epoca molto adoperato, Jean-Baptiste Biot incluse una descrizione del motore di Watt.

L'ingegnere dell'école Polytechnique Sadi Carnot (1796-1832) conosceva le innovazioni apportate da Watt e i più recenti sviluppi delle macchine ad alta pressione. In che misura egli abbia tratto ispirazione dalle caratteristiche di tali macchine è difficile da dire. In questi motori, in effetti, si anticipavano alcuni aspetti della sua teoria, come la necessità di una sorgente fredda e la fase di espansione del ciclo di Carnot; un'altra probabile fonte di ispirazione fu l'analogia, spesso utilizzata, tra le macchine a vapore e quelle idrauliche. Per esempio, dalla tradizione in campo idraulico venne il concetto di 'lavoro', o 'rendimento', che Watt misurava mediante un diagramma segreto e coperto da brevetto. Il motore di Newcomen, viceversa, ispirò la 'colonna di macchine ad acqua', che funzionava in modo abbastanza simile a una pompa invertita. Cosa ancor più importante, Carnot aveva familiarità con la teoria generale delle macchine formulata da suo padre e che, attraverso le analogie di cui sopra, veniva a porsi in relazione con la macchina a vapore.

Carnot pubblicò il famoso lavoro Réflexions sur la puissance motrice du feu nel 1824. La sua prima affermazione fondamentale fu che la produzione di lavoro con mezzi termici dipendeva da una differenza di temperatura che consentisse una 'cascata di calorico'. L'analogia con le macchine idrauliche suggerì poi che in una macchina ottimale non si dovesse avere alcun cambiamento di temperatura che non fosse associato a una variazione di volume della sostanza in gioco. Carnot descrisse il più semplice processo ciclico che soddisfaceva questo criterio: espansione isoterma di aria mediante contatto con una sorgente calda, aumento adiabatico di temperatura attraverso la compressione, contrazione isoterma mediante contatto con una sorgente fredda, ritorno adiabatico allo stato originale. Il ciclo descritto è reversibile.

Seguì il teorema più importante di Carnot: un motore reversibile possiede il massimo rendimento possibile tra tutti i motori che lavorano tra le stesse due temperature. La dimostrazione si basa su due assiomi: (1) la conservazione del calorico; (2) l'impossibilità di una specifica forma di moto perpetuo. Supponiamo, argomentava Carnot ricorrendo a un procedimento per assurdo, che esista un motore più efficiente di quello reversibile. Il lavoro prodotto da questo ipotetico motore sarebbe quindi superiore a quello necessario a riportare il calorico 'caduto' al suo livello originario mediante il motore reversibile funzionante in senso inverso. Il funzionamento simultaneo dei due motori, di conseguenza, consentirebbe la produzione indefinita di lavoro senza bisogno di alcuna compensazione. Allo scopo di evitare questa conseguenza, deve valere il teorema di Carnot.

Un corollario di questo teorema è che tutti i motori reversibili che lavorano tra le stesse due temperature hanno la medesima efficienza: il rapporto tra il lavoro prodotto e il calore trasferito è funzione soltanto delle due temperature (della sorgente calda e del 'pozzo' freddo). Carnot cercò di determinare questa funzione universale; a tale scopo, in linea di principio, è sufficiente conoscere le proprietà elastiche e termiche di un fluido con il quale si possa effettuare un ciclo di Carnot. Egli si rese conto che i dati disponibili all'epoca erano insufficienti per una tale determinazione completa. Comprese però che usando il suo teorema si potevano ricavare relazioni tra le proprietà costitutive dei fluidi e la funzione universale che dava il rendimento. Egli dimostrò, per esempio, che per qualsiasi gas che soddisfi la relazione PV=Rθ il calore necessario all'espansione isoterma è indipendente dalla natura del gas, ed è proporzionale al logaritmo del rapporto tra il volume iniziale e quello finale.

La sua dimostrazione si basava sull'esame di un ciclo effettuato sul gas, costituito da due isoterme alle temperature θ e θ+dθ, e da due trasformazioni adiabatiche operanti all'incirca ai volumi V1 e V2. Secondo il teorema di Carnot, il lavoro prodotto δW e il calore trasferito Q in questo ciclo sono legati dalla relazione δW/Q=μ(θ)dθ, dove μ(θ) è una funzione universale di θ (la cosiddetta 'funzione di Carnot'). Il lavoro δW è l'integrale di −PdV su tutto il ciclo, che vale Rdθln(V1/V2). Il calore Q è dato da (R/μ)ln(V1/V2).

Carnot si esprimeva più a parole che mediante formule e seguiva la tendenza dei suoi contemporanei di trascurare le deviazioni dalla legge PV=Rθ. Il suo ragionamento si generalizza facilmente a un fluido arbitrario. Si considerino a questo scopo il lavoro e il calore scambiati in un ciclo di Carnot infinitesimale e 'allungato', costituito da due isoterme alle temperature θ e θ+dθ e da due trasformazioni adiabatiche ai volumi approssimativi V e dV, in cui dθ è un infinitesimo di ordine superiore a V+dV.

Il lavoro compiuto è P(θ+dθ,V)dV−P(θ,V)dV, mentre il calore trasferito è ldV, in base alla definizione del calore latente di espansione l. Uguagliando il rapporto tra queste due quantità a μ(θ)dθ si ottiene la relazione

Questa importante relazione è nota in genere come 'formula di Carnot' (o di Carnot-Clapeyron), anche se fu Thomson a fornirne l'espressione generale. La formula di Carnot necessita soltanto del teorema di Carnot, senza bisogno di far ricorso né alla conservazione del calorico, né alle leggi di Boyle e di Gay-Lussac. Molti dei risultati ricavati da Carnot non possedevano questo livello di generalità e non sopravvissero al successivo abbandono del calorico. Ciononostante, il suo teorema, come pure il metodo utilizzato per dimostrarlo, avrebbero avuto un futuro brillante. Le macchine e i processi ideali, i cicli reversibili, i ragionamenti per assurdo nonché i principî generali divennero l'essenza della termodinamica moderna.

Il trattato di Carnot passò a lungo inosservato, probabilmente per ragioni simili a quelle che ritardarono l'accoglienza dei Principes di suo padre: era troppo astratto per incontrare il favore degli ingegneri e troppo lontano dagli interessi dei matematici francesi dell'epoca. Carnot non solo ignorò gli approcci 'molecolari' di Laplace, ma utilizzò l'analisi matematica con molta parsimonia, relegandola alle note del trattato. Nel 1834 Émile Clapeyron (1799-1864) tradusse i principali risultati di Carnot in termini di coefficienti differenziali e di diagrammi pressione-volume, portandoli così all'attenzione di una comunità più vasta. La fisica francese però a quel tempo stava ormai assumendo un atteggiamento empiristico, che confinava la teoria in un ruolo puramente descrittivo. Il suo astro nascente, Henri-Victor Regnault (1810-1878), si avvicinò ai fenomeni termici con una forte sfiducia nei confronti delle teorie precedenti e progettò i suoi accurati esperimenti in modo da limitarne al minimo l'uso. Negli anni Quaranta del XIX sec., grazie ai generosi finanziamenti del ministero dei Lavori Pubblici, egli iniziò una serie sistematica di misurazioni delle proprietà termiche del vapore e dei gas. I suoi risultati erano in contraddizione con le leggi stabilite in precedenza e fornirono dati durevoli per i fisici e gli ingegneri che si occupavano di produzione di potenza a vapore. Malgrado ciò, questi stessi risultati non ispirarono nuove teorie.

Il principio di conservazione dell'energia

Sadi Carnot, dopo aver pubblicato le Réflexions, si espresse negativamente, in alcuni scritti inediti, sulla teoria del calorico. Era a conoscenza degli esperimenti che Benjamin Thompson, conte di Rumford (1753-1814), aveva effettuato nel 1798, con le trivelle rotanti sul fondo dei tubi di cannone, ma non li considerava definitivi. Rumford era stato molto attento nell'escludere due possibili spiegazioni del riscaldamento del cannone basate sulla teoria del calorico (una semplice ridistribuzione del calore e un'alterazione della capacità termica del metallo nel processo di rotazione delle trivelle), ma questo non bastava. Come aveva già osservato il chimico francese Claude-Louis Berthollet (1748-1822), la costanza della capacità termica non escludeva un calore latente di transizione. Per questo motivo Carnot basò la confutazione della teoria del calorico sull'esistenza di processi in cui si innalza la temperatura di un gas effettuando su di esso del lavoro, ma senza cambiare la sua pressione. Come esempio tipico considerò l'espansione di un gas nel vuoto, seguita da una ricompressione adiabatica alla pressione originaria. La prima fase non implicava, come stabilito da un esperimento di Gay-Lussac, alcuna variazione globale di temperatura. Della seconda fase era invece ben noto che comportava un aumento della temperatura. In contrasto con la teoria del calorico, quindi, la temperatura di un gas a una certa pressione risultava indipendente dal suo contenuto di calore.

Il declino della teoria del calorico iniziò subito dopo queste considerazioni inedite. Nello stesso anno in cui Carnot morì, il 1832, André-Marie Ampère sostenne una teoria vibrazionale del calore, in sostituzione di quella del calorico, traendo ispirazione dalla nuova teoria della luce elaborata dal suo amico Augustin-Jean Fresnel e dalla ben nota analogia tra calore radiante e luce. Negli anni successivi il problema della natura del calore fu frequentemente oggetto di discussione, con un numero crescente di sostenitori dell'interpretazione cinetica in Francia, in Inghilterra e in Germania. James P. Joule (1818-1889), un birraio di Manchester con ambizioni filosofiche, abbracciò questo punto di vista anche se il suo insegnante privato di fisica, il famoso John Dalton, aveva sostenuto appassionatamente la teoria del calorico.

Le prime ricerche di Joule, pubblicate intorno al 1840 nella rivista semidivulgativa di John Sturgeon "Annals of electricity", erano motivate dalla diffusa speranza che i motori elettrici avrebbero soppiantato quelli a vapore. Con grande disappunto, Joule scoprì che lo zinco consumato per fornire corrente a un motore sarebbe costato molto di più del carbone necessario a un motore a vapore per effettuare lo stesso lavoro. I suoi esperimenti richiedevano di misurare il calore prodotto nel circuito, da cui derivò la legge che porta il suo nome. Nel 1843 dimostrò che il calore veniva 'creato' nel filo che portava corrente e non semplicemente ridistribuito da una parte a un'altra del circuito, o prodotto da un'alterazione dello stato del filo. La sorgente elettrica, una dinamo, richiedeva una quantità di lavoro proporzionale alla quantità di calore prodotta nel circuito. Joule misurò il coefficiente di proporzionalità e presto determinò questo 'valore meccanico del calore' anche in altri due modi: facendo passare dell'acqua attraverso capillari e mediante la compressione isoterma di un gas. Tuttavia, gli esperimenti erano ancora poco precisi e non vi era accordo tra i valori determinati con i diversi metodi.

Negli anni successivi Joule diede la preferenza al metodo basato sulla viscosità dell'acqua, poiché questo forniva l'esempio più nuovo e più chiaro della conversione del lavoro in calore e anche perché riteneva di poterlo perfezionare meglio. Utilizzando una ruota a pale, messa in movimento in una vasca calorimetrica dalla caduta di alcuni pesi, determinò alla fine un valore di 4,15 joule/caloria, espresso in unità di misura moderne (il valore accettato attualmente è 4,18 J/cal). L'esperimento richiedeva abilità termometriche straordinarie e un'attenzione estrema per annullare flussi di calore indesiderati o per correggerne l'effetto. È possibile che Joule abbia acquisito parte di queste abilità grazie alle sue conoscenze degli ultimi perfezionamenti della tecnica di produzione della birra, che necessitavano di un controllo preciso della temperatura delle sostanze sottoposte a fermentazione.

Benché Joule presentasse le sue ricerche in chiave sperimentale, di tanto in tanto accennava anche a motivazioni teoriche o teologiche. Era convinto che soltanto Dio potesse creare o annullare la forza viva. La materia, per come la immaginava Joule, era costituita da molecole, per le quali l''attrazione attraverso lo spazio' e la forza viva si potevano trasformare l'una nell'altra, ma erano nel complesso indistruttibili. Il calore era visto come un tipo di movimento delle molecole che, nell'evolversi delle sue concezioni, fu di volta in volta vibrazionale, rotazionale o traslazionale. La quantità di calore di una sostanza, essendo misurata dalla forza viva corrispondente, poteva variare solamente per effetto del lavoro effettuato da forze esterne, o per l'estinzione del calore latente che Joule, nel 1847, identificava con l'attrazione (potenziale di forze molecolari) attraverso lo spazio.

All'insaputa di Joule, nel 1842 un medico tedesco, Julius Robert von Mayer (1814-1878), aveva già affermato l'equivalenza tra calore e lavoro, fornendo una prima stima del fattore di conversione sulla base delle proprietà termiche dei gas. Mayer ricordava di essere stato stimolato da un'osservazione casuale fatta nel 1840 a Giava, ossia che il sangue venoso aveva un colore più chiaro nelle persone che vivono nei climi caldi. Ai suoi occhi questo fatto confermava la teoria, allora controversa, di Lavoisier, secondo la quale la respirazione era una forma di combustione, in cui la sostanza inspirata veniva bruciata producendo calore. Una temperatura esterna più alta comportava una minore combustione e quindi un sangue più pulito. Questa teoria implicava che si producesse una quantità fissa di calore per ogni data quantità di sostanza inspirata. Mayer proseguì quindi argomentando che il corpo umano avrebbe potuto nello stesso tempo produrre lavoro, che si sarebbe potuto convertire in calore per attrito. Ipotizzando che il calore totale così prodotto direttamente e indirettamente dal corpo fosse costante per una data quantità di sostanza inspirata (e ipotizzando anche implicitamente che l'attrito 'creasse' calore), Mayer concluse che il lavoro effettuato e il calore corrispondente fossero in rapporto costante.

Nel 1842 Mayer ricavò dunque il fattore di conversione tra calore e lavoro uguagliando il calore C_V, necessario a innalzare di un grado la temperatura di una massa unitaria di gas a volume costante, al calore C_P, necessario a realizzare lo stesso incremento di temperatura a pressione costante, diminuito dell'equivalente in calore del lavoro effettuato dal gas in quest'ultimo processo. In formule si ricava quindi l'equazione di Mayer J(C_P−C_V)=R, in cui R è la costante dei gas perfetti e J è il numero di unità di lavoro corrispondenti a un'unità di calore. I dati calorimetrici provenienti dalla Francia fornivano un valore J=3,60 joule/caloria (in unità moderne). Questo calcolo presupponeva la possibilità di connettere gli stati del gas dopo il riscaldamento isocoro e isobaro senza consumo di calore o lavoro. Come lo stesso Mayer spiegò nel 1845, l'espansione alla Gay-Lussac di un gas nel vuoto, non implicando variazioni di temperatura, forniva proprio il passaggio richiesto.

Mayer inquadrò, inoltre, l'equivalenza tra calore e lavoro in un principio generale di 'uguaglianza di causa ed effetto', in base al quale 'forze' mutuamente dipendenti come il lavoro, la forza viva e il calore possedessero equivalenti numerici. Egli d'altra parte non prese posizione sulla natura stessa del calore. Dove Joule vedeva una trasformazione della forza viva macroscopica in forza viva microscopica, Mayer individuava, invece, una creazione di calore determinata dalla distruzione di forza viva. È notevole il fatto che nel 1842 Mayer fosse convinto solo che non si potesse distruggere una forza senza che questa ricomparisse in qualche altra forma. Considerava la creazione di una forza un fenomeno non solo possibile, ma addirittura necessario, come nel caso del calore solare. Soltanto nel 1845 Mayer affermò un principio generale di conservazione della forza, considerando in questo caso il calore solare provocato da meteoriti.

Sia l'affermazione dell'equivalenza tra calore e lavoro sia l'enunciazione generale della conservazione della forza passarono quasi inosservate finché, nel 1854, non vennero riprese da Hermann von Helmholtz (1821-1894). Egli, come Mayer, era stato un medico, e formulò le sue prime considerazioni sulla conservazione della forza in un contesto di fisiologia; a differenza di Mayer, però, aveva una maggiore padronanza della fisica matematica e una posizione fermamente riduzionista in termini meccanici. La sua memoria del 1847 sulla conservazione della forza iniziava con un'introduzione kantiana, in cui cercava di dimostrare che una piena comprensibilità della Natura richiedeva che essa fosse riducibile all'azione di forze centrali tra coppie di punti materiali. Questa riduzione implicava l'esistenza di un potenziale per le forze, la conservazione della somma del potenziale totale e della forza viva totale, e l'impossibilità del moto perpetuo. Helmholtz cercò di dimostrare anche l'implicazione inversa, ossia che l'impossibilità del moto perpetuo comportava la riducibilità a sole forze centrali. In questo contesto dimostrò sia familiarità con il concetto di 'lavoro' elaborato in Francia, sia una propensione per la fisica molecolare di stile laplaciano.

La parte più ampia, e più durevole, della memoria di Helmholtz consisteva nella formulazione precisa in termini fisico-matematici della nuova legge di conservazione in ogni ambito della fisica. In alcuni settori, come la gravitazione o l'elettrostatica, la riduzione a forze centrali era già stata operata, cosicché l'identificazione della quantità conservata era semplice e diretta. In altri casi, come quello dell'elettrodinamica, non si disponeva ancora di una simile riduzione; Helmholtz usò quindi la conservazione della forza come un vincolo sulla forma delle leggi fisiche in termini macroscopici. Per esempio, ricavò l'induzione elettromagnetica dall'esistenza delle forze elettromagnetiche ipotizzando che il calore di Joule prodotto in un filo conduttore chiuso in movimento in prossimità di un magnete fosse uguale al lavoro necessario a muovere il filo (tale impostazione non è corretta, in quanto non tiene in considerazione la possibilità di un'energia interna del sistema costituito dal filo chiuso e dal magnete interagenti; per una fortunata coincidenza, nel caso particolare questa energia risulta costante). Questo tipo di ragionamenti era alla base di un genere di fisica basata su principî generali, che Helmholtz portò avanti per tutta la vita.

Nel capitolo della sua memoria dedicato al calore, Helmholtz si dichiarò a favore della teoria cinetica, che gli era familiare dagli anni del ginnasio. Nel farlo, richiamò le ragioni a sfavore della teoria del calorico, e citò la determinazione pionieristica dell'equivalente meccanico della caloria da parte di Joule. Elogiò quindi Carnot e Clapeyron per aver fornito il primo esempio notevole di come si potesse utilizzare l'impossibilità del moto perpetuo quale vincolo imposto alle leggi fisiche, anche se condannò il fondamento dato da Carnot ai suoi risultati, basato sul calorico. Nell'eventualità che il teorema e la relazione [1] di Carnot potessero sopravvivere all'abbandono del calorico, Helmholtz combinò quest'ultima con la relazione di Carl Holtzmann Jl=P, ottenendo μ=J/θ per la funzione di Carnot. Anche se Holtzmann aveva usato la sua relazione nel contesto della teoria del calorico, egli era convinto che la sua corretta giustificazione appartenesse alla teoria cinetica del calore: il calore di espansione isoterma JldV avrebbe dovuto uguagliare il lavoro di espansione PdV se l'energia potenziale delle interazioni molecolari fosse risultata trascurabile. Helmholtz ottenne quindi la prima determinazione corretta della funzione di Carnot; non aveva d'altra parte alcuna idea di come riconciliare la teoria di Carnot con la concezione cinetica del calore.

Joule, Mayer e Helmholtz sono considerati generalmente i principali artefici del principio di conservazione dell'energia. D'altra parte le loro diverse motivazioni condussero questi studiosi a formulare il principio in modi diversi, e anche la diffusione delle loro idee non fu senza ostacoli. Joule ebbe difficoltà a far approvare il suo lavoro dalle autorità della Royal Society; la memoria di Helmholtz fu rifiutata dagli "Annalen der Physik" e all'inizio ricevette più critiche che elogi; l'articolo di Mayer apparve come una speculazione dilettantistica alla maggior parte dei suoi contemporanei. Con l'eccezione di Helmholtz, i sostenitori più attivi della fisica basata sul concetto di energia non furono i suoi inventori. Fu un piccolo gruppo di filosofi naturali inglesi, quali William Thomson, Peter Guthrie Tait, William Rankine e James C. Maxwell, a percepire con maggior chiarezza i vantaggi teorici e pratici di questo nuovo tipo di fisica e a mettere in campo sforzi intensi a livello politico e istituzionale per rimpiazzare il vecchio stile della fisica basata sul concetto di forza. Nel 1851 Thomson introdusse il significato, oggi consueto, di 'energia' come capacità di compiere lavoro, e divenne presto il leader inglese di un nuova 'fisica dell'energia'.

I principî della termodinamica

William Thomson (1824-1907) era un matematico formatosi a Cambridge, dotato di uno spiccato interesse per i problemi pratici, grazie al suo passaggio per l'Università di Glasgow e alla stretta relazione con il fratello James, ingegnere. I due fratelli assimilarono dal loro professore d'ingegneria di Glasgow e dal loro amico Lewis Gordon l'idea di Poncelet che il lavoro, o 'effetto meccanico' secondo la terminologia di Gordon, non si potesse annullare, ma solo dissipare. Al pari di Descartes, Joule e Saint-Venant, Thomson riservava la Creazione a Dio. Verso la fine del decennio 1840-1850, egli applicò il 'principio dell'effetto meccanico' all'elettricità, fornendo con ciò sia una definizione dell'energia potenziale e della forza elettromotrice basata sul concetto di energia, sia una deduzione dell'induzione elettromagnetica simile a quella di Helmholtz. Per Thomson, come per Poncelet, qualunque perdita di effetto meccanico non poteva che essere apparente. Il fatto che in alcuni casi, come per l'acqua che irrompe in una chiusa e poi raggiunge lo stato di quiete, non sembrasse esservi alcuna compensazione per la perdita di moto, costituiva per lui e per suo fratello un mistero.

Thomson iniziò a interessarsi al funzionamento dei motori a vapore in seguito alle conversazioni con il fratello James, e in occasione di una sua visita al laboratorio di Regnault nel 1845; lesse in quel periodo la memoria di Clapeyron e ammirò la potenza e l'ampiezza del ragionamento di Carnot. Nel 1848 propose una scala assoluta di temperatura, in cui il grado era definito "dall'effetto meccanico che si ottiene dalla diminuzione di un'unità di calore". Tale definizione è incompatibile con quella termodinamica fornita in seguito dallo stesso Thomson, poiché implica μ(T)=T invece di μ(T)=1/T. Nel 1849 tentò di ricavare la funzione μ di Carnot attraverso le misure di Regnault sul vapore, utilizzando l'ipotesi che il vapore saturo seguisse approssimativamente la legge dei gas perfetti e usando la

in cui L_v è il calore latente di vaporizzazione, P_s la pressione di vapore saturo, ϱ_v la densità del vapore e ϱ_a la densità dell'acqua. Questa relazione deriva dal teorema di Carnot applicato a un ciclo di Carnot infinitesimale con coesistenza di vapore e acqua. Il fratello James ricavò poco tempo dopo la relazione analoga

che determina l'abbassamento del punto di fusione θ_f del ghiaccio in termini di calore latente di fusione L_f, densità dell'acqua ϱ_a e densità del ghiaccio ϱ_g. La conferma di questa relazione a opera di William ebbe l'effetto di accrescere la fiducia dei fratelli Thomson nella validità della teoria di Carnot.

Nello stesso tempo, William Thomson apprezzava la qualità degli esperimenti di Joule favorendone il riconoscimento; accolse positivamente l'idea della generazione di calore attraverso la semplice agitazione dell'acqua, che risolveva il paradosso dell'acqua nella chiusa; trovava tuttavia difficile accettare l'idea inversa, secondo la quale si poteva trasformare il calore in lavoro, poiché questo minava le basi del ragionamento di Carnot. Il compromesso adottato da Thomson, per cui il calore poteva essere creato ma non distrutto, conduceva a nuovi paradossi. Come notò Joule, se il calore veniva conservato in un ciclo di Carnot e poteva essere creato mediante attrito, il lavoro fornito da un motore di Carnot si sarebbe potuto convertire in calore e il calore totale dell'Universo sarebbe così aumentato ad libitum. Thomson stesso rilevò un conflitto paradossale con il principio dell'effetto meccanico:

Quando l''agente termico' [una differenza di temperatura] […] viene impiegato per condurre calore attraverso un solido, che ne è dell'effetto meccanico che esso potrebbe produrre? Nulla può andare perduto nel funzionamento della Natura ‒ nessuna porzione di energia si può distruggere […]. Può sembrare che si possa superare completamente la difficoltà abbandonando il postulato fondamentale di Carnot [la conservazione del calore durante la sua 'caduta']; visione questa, fortemente incoraggiata dal signor Joule […]. Se operiamo così, però, ci scontriamo con innumerevoli altre difficoltà ‒ insuperabili in mancanza di altri studi sperimentali e di una totale ricostruzione della teoria del calore dalle sue fondamenta. È in realtà agli esperimenti che dobbiamo guardare, o per una verifica del postulato di Carnot e una spiegazione delle difficoltà che abbiamo considerato, o per un fondamento completamente nuovo della teoria del calore. (Thomson 1849 [1882, pp. 118-119])

Thomson analizzò inutilmente, con questo suo atteggiamento empirista, i dati di Regnault sul vapore. La vera soluzione del paradosso risiedeva in una modifica del ragionamento teorico di Carnot, come spiegò Rudolf Clausius (1822-1888) nella memoria del 1850 dal titolo Über die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen (Sulla forza motrice del calore e le leggi che se ne possono dedurre per la teoria del calore). Clausius, all'epoca semplice Privatdozent presso l'Università di Berlino, osservò che si poteva ammettere contemporaneamente, in una macchina di Carnot, il trasferimento di calore dalla sorgente calda a quella fredda e la trasformazione di parte del calore in lavoro. Si poteva dunque preservare il teorema di Carnot, senza contraddire l'affermazione di Joule sull'equivalenza tra calore e lavoro. Non era più possibile però basare il teorema sull'impossibilità del moto perpetuo. Imitando il ragionamento per assurdo di Carnot, Clausius ipotizzò l'esistenza di una macchina termica che funzionasse tra due temperature e che avesse un rendimento maggiore di una macchina di Carnot reversibile. Il lavoro prodotto da questa ipotetica macchina si sarebbe potuto usare per far funzionare una macchina di Carnot a ciclo inverso tra le stesse sorgenti. Il risultato netto sarebbe stato un trasferimento di calore da una sorgente fredda a una calda senza alcuna compensazione. L'impossibilità di un tale trasferimento, che divenne il fondamento della formulazione di Clausius, implica il teorema di Carnot.

Poiché questa impossibilità si accordava con il 'comportamento noto del calore', Clausius prese il teorema di Carnot come suo secondo principio. Il primo consisteva in una versione dell'equivalenza di Joule tra calore e lavoro: "In tutti i casi in cui il calore produce lavoro, si consuma una quantità di calore proporzionale al lavoro prodotto e, inversamente, si può produrre la stessa quantità di calore consumando una uguale quantità di lavoro" (Clausius 1850 [1867, p. 18]). Questo principio contraddiceva, come notò lo stesso Clausius, l'idea generalmente accettata di un 'contenuto di calore' totale di un sistema, secondo la quale il calore acquistato durante un certo processo dipendeva soltanto dallo stato iniziale e finale del sistema stesso. Seguendo il modello di Clapeyron, Clausius applicò questo postulato a un ciclo infinitesimale di Carnot e ottenne così una relazione differenziale tra i calori specifici. Da questa dedusse che la forma

[2] dU=δQ+δW

doveva essere un differenziale esatto (da ora in poi il calore sarà espresso direttamente nelle stesse unità di misura del lavoro). Clausius non fornì un'interpretazione della funzione U. Introdusse invece il lavoro dw delle forze interne e interpretò la differenza dY=dU−dw come il calore libero contenuto nel corpo. Egli ipotizzò inoltre che in un gas poco denso le forze intermolecolari non compissero lavoro durante l'espansione, il che rende U funzione della sola temperatura. Da ciò consegue la relazione di Holtzmann l=P. La relazione di Carnot [1] rimaneva ancora valida, dipendendo soltanto dalla validità del teorema di Carnot. Queste due formule, insieme all'equazione dei gas perfetti, danno μ=1/θ, coerentemente con i risultati precedenti di Helmholtz (che Clausius tuttavia non citò). Clausius verificò che i dati di Regnault sul vapore erano compatibili con questa espressione della funzione di Carnot.

La memoria di Clausius stabilì il fondamento della termodinamica moderna sulla base di due principî e dei vincoli sulle proprietà costitutive che da questi stessi principî derivano. Il suo approccio era prevalentemente macroscopico, con un puntuale riferimento alla rappresentazione cinetico-molecolare dei gas che servì a mettere in relazione la funzione universale di Carnot con la temperatura del gas ideale.

Nel 1851, dopo aver letto Clausius, Thomson stabilì un principio fondante simile, utilizzando la teoria dinamica del calore, ma con alcune differenze. Diversamente da Clausius, egli utilizzò le nozioni di integrale ciclico e di differenziale esatto per ricavare i vincoli sulle proprietà costitutive e, cosa più importante, mise in relazione la prima legge della termodinamica con il suo principio dell'effetto meccanico, introducendo il termine 'energia' nella sua accezione tecnica moderna e definì l'energia interna di un sistema. Thomson argomentò che il principio dell'effetto meccanico implicava che il lavoro totale delle forze esterne agenti su un sistema dovesse uguagliare la variazione della sua energia cinetica, diminuita del lavoro delle relative forze interne del sistema. Questo lavoro totale, di conseguenza, si annulla in un ciclo del sistema (purché le forze interne derivino da un potenziale); esso comprende il lavoro delle relative forze macroscopiche e quello delle forze microscopiche responsabili degli scambi termici. Quindi la somma del lavoro e del calore scambiato (espresso nelle unità di misura del lavoro) si annulla in un ciclo, secondo la riformulazione di Thomson che precisava la legge di equivalenza di Joule. Tale postulato implica, come notò inoltre Thomson, che la somma del lavoro e del calore scambiato da un sistema in un processo non ciclico dipende soltanto dagli stati iniziale e finale del sistema. Partendo da uno stato di riferimento, Thomson fornì quindi una definizione operativa dell''energia meccanica' di un sistema in un dato stato come il valore di questa somma per qualsiasi processo che conduca dallo stato di riferimento a quello in questione.

Un'altra differenza tra Thomson e Clausius risiedeva nella formulazione del secondo principio. Utilizzando un'altra versione del ragionamento per assurdo di Carnot, il calore prelevato dalla sorgente calda da parte dell'ipotetica macchina termica superiore a quella reversibile poteva essere recuperato facendo funzionare al contrario una macchina di Carnot. Dal momento che il lavoro richiesto da quest'ultima è inferiore a quello necessario a far funzionare la macchina termica ipotetica, sarebbe possibile produrre lavoro prelevando calore da una singola sorgente. La formulazione di Thomson del secondo principio afferma l'impossibilità di una simile produzione di lavoro grazie a un'unica temperatura: "È impossibile produrre, mediante mezzi materiali inanimati, alcun effetto meccanico da qualsiasi porzione di materia raffreddandola al di sotto della temperatura del più freddo degli oggetti circostanti" (Thomson 1851 [1882, p. 179]).

L'anno successivo Thomson stabilì una relazione tra il secondo principio e il comportamento irreversibile. Nella formulazione del suo paradosso del 1848 si era chiesto cosa ne sarebbe stato, nella conduzione termica da una sorgente calda a una fredda, del lavoro che si sarebbe potuto altrimenti produrre. Nella sua nuova teoria del calore, il conflitto con il principio dell'effetto meccanico scompariva, poiché il lavoro prodotto da una macchina termica appariva ora equivalente a una perdita netta di calore da parte delle sorgenti. Rimaneva vero, però, che il calore scambiato non poteva più essere utilizzato per agire su una macchina termica, poiché in base al secondo principio un motore che sfruttasse una sola temperatura era impossibile. Thomson espresse questo dualismo con due affermazioni: "Il potere creatore di per sé può generare o distruggere energia […]. C'è attualmente una tendenza universale in natura alla dissipazione dell'energia meccanica" (Thomson 1852 [1882, p. 514]).

Per dissipazione s'intendeva una trasformazione tale che non fosse possibile ripristinare lo stato iniziale senza qualche compensazione, come nel caso di una macchina irreversibile, nella conduzione del calore o nell'assorbimento della luce. Per motivi teologici, Thomson non esitò ad applicare il principio all'intero Universo, e arrivò a predire che la Terra sarebbe prima o poi diventata inadatta a ospitare l'uomo, provocando con ciò grandi discussioni pubbliche.

Un'ultima differenza tra le prime ricerche di Thomson e di Clausius in termodinamica riguardava le diverse strategie seguite per determinare la funzione di Carnot. Tenendo presente il quadro offerto dalla teoria cinetica dei gas, Clausius non dubitava del fatto che la formula di Holtzmann fosse corretta e così anche la conseguenza che ne derivava, μ=1/θ. Thomson, che in quel periodo preferiva la rappresentazione dei gas nei termini dei vortici molecolari di Rankine, non aveva un'analoga predisposizione teorica e si affidava esclusivamente agli esperimenti per la determinazione di μ. Le misure di Regnault sul vapore, con l'ipotesi (errata) che il vapore saturo seguisse approssimativamente la legge dei gas perfetti, portavano a un valore di μ molto diverso da quello di Clausius. Per fortuna Thomson si rivolse a verifiche più dirette dell'ipotesi di Clausius, basate sulla variazione di temperatura δθ di un gas fatto passare attraverso una membrana porosa grazie a una differenza di pressione δP. Dall'applicazione dei due principî della termodinamica a questo processo adiabatico Thomson ricavò la relazione:

Di conseguenza, per un gas che obbedisca alla legge PV=Rθ la variazione di temperatura dipende da quanto la funzione di Carnot μ differisce dal valore di Clausius 1/θ. La lunga serie di accurate misurazioni compiute da Thomson e Joule confermò l'ipotesi di Clausius e permise di ricavare le correzioni appropriate per i gas reali.

Come Thomson osservò nel 1854, è possibile definire la temperatura T in modo che la relazione μ=1/T valga in modo esatto, il che implica, insieme al primo postulato, che valga la relazione Q1/T1+Q2/T2=0 per un ciclo di Carnot in cui vengano scambiate le quantità di calore Q1 e Q2 tra le sorgenti a temperature T1 e T2. Per un ciclo reversibile in cui venga scambiato calore con un numero arbitrario di sorgenti, Thomson ricavò inoltre la formula ∑Q_i/T_i=0, che egli considerava "l'espressione matematica del secondo principio". Applicando successivamente la termodinamica allo studio della termoelettricità e dell'elasticità, egli utilizzò direttamente questa formula al posto dei cicli infinitesimali di Carnot che avevano caratterizzato gli inizi della termodinamica.

Nello stesso anno Clausius pubblicò una memoria intitolata Über eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie (Su una formulazione modificata del secondo principio della teoria meccanica del calore), intendendo con questa chiarire la relazione esistente tra il primo e il secondo principio, esprimendo entrambi in termini di vincoli sulle quantità di calore rilasciate da sorgenti a temperature diverse attraverso un processo ciclico. Il primo principio afferma che il calore totale rilasciato uguaglia il lavoro compiuto nel processo, W=−Q, e implica l'esistenza di una funzione U di due stati del sistema, che esprime il valore di W+Q per qualsiasi trasformazione che porti dal primo al secondo stato e che Clausius in seguito, d'accordo con Thomson, chiamerà 'energia'. Nel caso più semplice, di un ciclo di Carnot, il secondo principio (insieme al primo) richiede che il rapporto tra le quantità di calore scambiate dalle due sorgenti sia una funzione data delle loro temperature. Clausius voleva generalizzare questo risultato a un numero qualsiasi di sorgenti di calore e lo fece mediante un procedimento particolare, scomponendo le variazioni di calore per le sorgenti in due tipi di trasformazioni: la conversione del calore da una delle sorgenti in lavoro (oppure viceversa) e il trasferimento di calore tra una coppia di sorgenti. È chiaro come egli fosse ancora influenzato dalla rappresentazione di Carnot della perdita di calore quale equivalente alla produzione di lavoro in un ciclo di Carnot.

In generale, Clausius definì l'equivalenza tra due trasformazioni mediante la condizione che la prima, combinata con l'inverso della seconda, si potesse realizzare per mezzo di un processo ciclico reversibile. Definì quindi numericamente il 'valore di una trasformazione' in modo tale che i valori di due trasformazioni equivalenti fossero uguali (primo postulato), e che il valore della combinazione di due trasformazioni fosse uguale alla somma dei valori delle due trasformazioni (secondo postulato). È possibile a questo punto semplificare il ragionamento di Clausius, abbandonando la distinzione tra i due tipi di trasformazioni e considerando solo le quantità di calore fornite dalle diverse sorgenti. In base al secondo postulato, il valore della trasformazione consistente nel rilascio della quantità Q di calore da parte della sorgente a temperatura θ deve essere della forma Qf(θ). Il valore di una trasformazione che coinvolga due sorgenti θ1 e θ2 è della forma Q1f(θ1)+Q2f(θ2). Si supponga ora che tale trasformazione sia realizzabile mediante un ciclo di Carnot: il suo valore, in accordo con il primo postulato, dovrebbe essere nullo. Il confronto con la relazione Q1/T1+Q2/T2=0, in cui T è la temperatura del gas perfetto (o temperatura assoluta di Thomson), implica che f(T) sia proporzionale a 1/T.

Clausius derivò così l'espressione generale ∫δQ/T per il valore equivalente di una trasformazione arbitraria in cui avvenga lo scambio della quantità di calore δQ attraverso una serie continua di sorgenti.

Per una trasformazione che sia realizzabile attraverso un processo ciclico reversibile, il valore totale deve essere nullo; Clausius considerò quest'ultima formulazione come 'l'espressione analitica del secondo principio della teoria meccanica del calore'. Per una trasformazione effettuata attraverso un ciclo di una macchina irreversibile, il valore totale deve essere negativo; se non lo fosse, tale trasformazione si potrebbe scomporre in una di valore nullo e in una per la quale le variazioni di calore δQ sono tutte positive, cosicché si potrebbe produrre lavoro senza la compensazione di un trasferimento di calore.

Clausius prese quindi in considerazione una sostanza soggetta a un ciclo reversibile. In questo caso, le temperature assunte in successione dalla sostanza sono uguali a quelle delle sorgenti con le quali essa scambia calore; il valore corrispondente della trasformazione deve quindi essere nullo. Siccome questo deve valere per qualsiasi ciclo, la grandezza δQ/T deve essere un differenziale esatto. Clausius utilizzò questa proprietà come metodo semplice per ricavare la formula di Carnot-Clapeyron. In seguito, nel 1865, Clausius introdusse il termine 'entropia', dal greco τϱοπή (trasformazione), per indicare l'integrale di questa forma differenziale a partire da uno stato di riferimento; analizzò anche transizioni irreversibili della sostanza da uno stato di equilibrio a un altro. La stessa sostanza poteva essere ricondotta allo stato originario mediante una trasformazione reversibile; lungo il ciclo risultante deve valere la disuguaglianza

[4] ∫δQ/T<0,

da cui segue che l'entropia del sistema complessivo comprendente la sostanza e tutte le sorgenti può solo aumentare, mentre la sua energia rimane ovviamente invariata. Le conclusioni di Clausius sono contenute in due affermazioni cosmiche, nello stile di Thomson: "L'energia dell'Universo è costante"; "L'entropia dell'Universo tende a un massimo" (Clausius 1865, p. 365).

Per comprendere meglio il significato dell'entropia, Clausius fece ricorso al concetto, da lui introdotto in precedenza, di 'disgregazione'. Era stato a lungo convinto, come spiegò nel 1862, che la capacità di produrre lavoro da parte di una sostanza scaldata a una certa temperatura dovesse risultare proporzionale a quella temperatura. Questo preconcetto, in linea con l'impostazione di Carnot, comportava che la somma δw+δW del lavoro interno e di quello esterno dovesse potersi esprimere nella forma TdZ, dove Z è una funzione di stato. Clausius chiamò Z la 'disgregazione', poiché essa fornisce 'il grado di dispersione delle molecole del corpo'. Questa è legata all'entropia S e alla quantità di calore Y interno dalla relazione dS=dZ+dY/T. Tale concetto non sopravvisse a Clausius; la maggior parte degli studiosi che contribuì ai primi sviluppi della termodinamica era contraria alle definizioni che non possedessero una controparte sperimentale, o che avessero delle somiglianze con la teoria del calorico. Il fisico americano Josiah W. Gibbs (1839-1903) rappresentò un'eccezione e osservò che il concetto di 'disgregazione' di Clausius anticipava un risultato della meccanica statistica, secondo il quale l'entropia di una sostanza si deve poter esprimere come somma di una funzione della sola temperatura e di una funzione dipendente dalla distanza tra le molecole. Thomson e Tait ragionavano piuttosto in termini di energia dissipata e di energia disponibile, nozioni queste che determinavano la capacità da parte dell'uomo di utilizzare l'energia per i suoi scopi.

Un altro contributo importante ai primi sviluppi della termodinamica venne dall'ingegnere scozzese William Rankine (1820-1872) il cui ruolo in questa vicenda è stato spesso considerato irrilevante, poiché il suo approccio appariva in opposizione con lo spirito fenomenologico della nuova termodinamica e il suo stile poteva risultare oscuro anche ai suoi stessi contemporanei. Malgrado ciò, Rankine nel 1850 ricavò, indipendentemente da Clausius e basandosi sul modello dei vortici molecolari, una serie di relazioni tra i 'coefficienti costitutivi' di una sostanza, che contenevano non espressamente tutte le implicazioni della moderna termodinamica. Nel 1853 Rankine riformulò i suoi risultati in una forma che appariva meno dipendente dalle ipotesi molecolari e introdusse l'integrale che dà l'entropia di una sostanza. Coniò anche i termini 'energia cinetica' ‒ tuttora in uso ‒ ed 'energia latente', che sarebbe presto diventata 'energia potenziale'. Infine, giocò un ruolo rilevante nella diffusione della nuova fisica dell'energia nella comunità ingegneristica in Inghilterra.

Anche se Clausius, Thomson e Rankine definirono principî e metodi della termodinamica, sarebbe errato attribuire a essi la sua formulazione definitiva. Le critiche successive e le nuove applicazioni contribuirono a chiarire il significato dei principî, a perfezionare il formalismo matematico, a eliminare nozioni superflue e a introdurre concetti nuovi e utili, come i potenziali termodinamici. Abbiamo già menzionato la caduta in disuso dei concetti di 'calore interno' e di 'disgregazione' di Clausius. Riguardo al significato dei principî, la versione di Clausius del secondo principio risultò meno ovvia di quanto egli avesse originariamente ritenuto. Per esempio, nel rispondere a un'obiezione di Gustave Adolphe Hirn, Clausius spiegò nel 1863 che la 'compensazione' necessaria per trasferire calore da un corpo freddo a uno caldo non doveva necessariamente essere di natura meccanica: poteva trattarsi di una variazione di temperatura di altri corpi. Gli autori che si occuparono di termodinamica verso la fine del XIX sec., come Max Planck, Pierre-Maurice-Marie Duhem e Jules-Henri Poincaré, eliminarono altri punti oscuri nella definizione di entropia, nel significato della reversibilità e nella distinzione tra le proprietà della sorgente e quelle del sistema.

Dal punto di vista matematico, i testi originali di Clausius risentivano della mancanza di una notazione specifica per le derivate parziali e utilizzavano la notazione fuorviante C=dQ/dθ per la capacità termica. Holtzmann rigettò così l'equazione di Clausius d(dQ/dV)/dθ−d(dQ/dθ)/dV=R/JV (applicazione del primo principio a un ciclo di Carnot infinitesimale) come un'assurdità matematica. La notazione dQ/dθ fu presto abbandonata, ma si conservò a lungo, fino al secolo successivo, la notazione dQ o dW, che confonde la forma differenziale con il differenziale esatto. Ferdinand Reech fu il solo che, a partire dal 1850 ca., utilizzò il simbolo δ per distinguere le forme differenziali dai differenziali esatti.

Malgrado queste vicissitudini, intorno al 1880 la termodinamica era ormai una scienza ben consolidata che si era dimostrata fertile in diversi ambiti della fisica, veniva insegnata nelle università e di essa esistevano notevoli trattati come quelli di Tait, Maxwell, Clausius e Carl Neumann.

Sviluppi

Coerentemente con la sua origine storica, la prima applicazione della termodinamica riguardò i gas e le transizioni di fase. Thomson estese ben presto le sue applicazioni alla termoelettricità, come ben si addiceva a uno studioso esperto sia nel campo della termologia sia in quello dell'elettricità. Dal primo principio egli dedusse il fatto che la forza elettromotrice di Seebeck E(T1,T2) in un circuito composto da due diversi conduttori metallici, con giunzioni alle temperature T1 e T2, era pari alla differenza tra le quantità di calore Π(T1) e Π(T2) sviluppate per effetto Peltier nelle due giunzioni (nelle unità di misura del lavoro), sommata a una quantità aggiuntiva di calore causata dal gradiente di temperatura lungo i due fili (chiamato ora 'calore di Thomson'). Thomson immaginò quindi una dinamo inserita nel circuito, in modo da controbilanciare quasi esattamente la forza di Seebeck; poiché la dissipazione per effetto Joule diventava in questo modo trascurabile, il processo risultava quasi reversibile e si poteva applicare l'equazione ∫δQ/T=0. Thomson ottenne così un'altra relazione tra la forza elettromotrice di Seebeck, il calore di Peltier e il calore di Thomson, e insieme alla precedente ne trasse l'utile formula

notò inoltre che i dati sperimentali disponibili richiedevano un effetto Thomson non nullo e fornì di ciò dimostrazione diretta nel 1856.

La base dei ragionamenti di Thomson sulla termoelettricità e sulla termoelasticità rimaneva l'annullamento di due integrali, quello della quantità δQ+δW lungo un processo ciclico e quello della quantità δQ/T su un processo ciclico reversibile; la funzione entropia non veniva utilizzata e i processi irreversibili non giocavano alcun ruolo: l'affermazione di Clausius sull'aumento di entropia nell'Universo non aveva in questo contesto alcuna applicazione pratica.

È significativo il fatto che soltanto negli anni Settanta del XIX sec. comparissero metodi nuovi nello studio della termodinamica. In Francia, l'ingegnere François Massieu (1832-1896) introdusse la fonction charactéristique ψ=S−U/T, funzione delle variabili T e V. Se ψ è nota, rilevò Massieu, il differenziale dψ=(U/T2)dT+(P/T)dV fornisce U e P come funzioni di T e V, da cui derivano tutte le altre proprietà termodinamiche del sistema. La funzione S−(U+PV)/T, dipendente dalle variabili T e P, offre la stessa potenzialità. Nel suo primo articolo, nel 1873, Gibbs illustrò l'utilità di scegliere S e V come variabili di stato per una sostanza omogenea e le utilizzò per una rappresentazione grafica delle sue diverse fasi (liquido, solido, vapore).

Della massima importanza fu l'articolo On the equilibrium of heterogeneous substances che Gibbs pubblicò nel 1875 servendosi, ispirato dalla legge di Clausius sull'aumento dell'entropia, del principio secondo il quale l'entropia di un sistema chiuso in equilibrio deve assumere un valore massimo, rispetto a qualsiasi variazione di stato del sistema. Per poter applicare tale principio a una miscela di componenti omogenee, Gibbs espresse l'energia di questa come funzione di S, V e delle masse m1, m2, ..., m_i, ... delle componenti, in modo che risultasse

[6]  dU=TdS-PdV+∑μ_idm_i,

dove μ_i rappresenta i potenziali elettrochimici delle relative componenti. In base al principio di Gibbs, l'equilibrio di tale sistema richiede che la sua entropia assuma un valore massimo, rispetto a qualsiasi variazione di stato derivante da transizioni di fase o da reazioni chimiche virtuali, con energia e volume costanti. Dunque dS=0 quando dU=0 e dV=0, quindi ∑μ_idm_i=0 per qualsiasi variazione virtuale delle masse, compatibile con le leggi di conservazione della miscela. Per esempio, per una reazione chimica, scritta in notazione algebrica ∑a_iK_i=0 (come la reazione 2H₂+O₂→2H₂O, scritta 2H₂+O₂−2H₂O=0), questa condizione porta all'equazione ∑a_iμ_i=0. Nel caso più generale si arriva alla 'regola delle fasi', secondo la quale il numero di variabili di stato indipendenti del sistema in equilibrio è n+2−r, dove r indica il numero di fasi e n il numero di componenti indipendenti.

Gibbs pubblicò queste considerazioni, e molto altro, nelle "Transactions of the Connecticut Academy", che non avevano grande diffusione. Maxwell, che ne aveva ricevuto una copia, le utilizzò tessendone le lodi; esse però rimasero in gran parte ignorate ancora per alcuni anni, in primo luogo a causa della propensione di Gibbs per una generalità astratta, il che rendeva i suoi scritti illeggibili tanto per i chimici quanto per i fisici sperimentali. Un altro motivo risiedeva in una radicata tradizione in termochimica, secondo la quale le affinità chimiche dipendevano solo dai calori di reazione. Questa idea, sviluppata dal chimico danese Julius Thomsen negli anni Cinquanta e dal chimico francese Marcellin Berthelot (1827-1907) negli anni Sessanta, sembrava confermata in larga misura dagli esperimenti. Berthelot era consapevole di alcune eccezioni al suo 'principio di lavoro massimo', per esempio l'esistenza di processi endotermici spontanei, che giustificava ammettendo l'esistenza di processi fisici simultanei capaci di assorbire calore.

Nel decennio 1870-1880, diverse ricerche in termodinamica minarono la validità della distinzione netta operata da Berthelot tra processi fisici e processi chimici. Oltre al lavoro di Gibbs, vi erano le analogie proposte da August Friedrich Horstmann (1842-1929) tra la dissociazione e le transizioni di fase e l'idea avanzata da John W. Strutt (lord Rayleigh; 1842-1919) che la dissipazione fosse alla base delle reazioni chimiche. Fu tuttavia Helmholtz ad abbattere in modo definitivo la vecchia termochimica, nel 1882. Studiando le anomalie elettrochimiche, egli si era convinto che l'entropia giocasse un ruolo essenziale nelle reazioni chimiche e introdusse il concetto di 'energia libera'

[7] F=U−TS,

la cui variazione a temperatura costante fornisce il 'lavoro convertibile' compiuto sul sistema (−PdV se la pressione è la sola forza agente) e dimostrò che F deve assumere un valore minimo in una miscela di reagenti chimici, per volume e temperatura fissati. Ricavò così condizioni di equilibrio simili a quelle trovate da Gibbs, anche se con un minore grado di generalità. Jacobus Henricus van't Hoff, Planck e Duhem svilupparono ulteriormente la termodinamica chimica, che intorno agli anni Novanta dell'Ottocento divenne una componente essenziale della fisica chimica, istituzionalizzata da Friedrich Wilhelm Ostwald e Walther Nernst.

Berthelot e i suoi allievi francesi continuarono comunque a sostenere la validità del principio di lavoro massimo. Essi argomentavano che l'introduzione dell'entropia non migliorava il valore della termochimica dal punto di vista empirico, poiché l'entropia delle sostanze risultava in generale inaccessibile alle misure.

La risposta definitiva a questa obiezione fu il principio enunciato da Nernst nel 1906, chiamato a volte 'terzo principio della termodinamica', secondo il quale la variazione di entropia in qualsiasi reazione chimica si annulla al tendere della temperatura a zero. La variazione di entropia ΔS a temperatura T si può ricavare dall'integrale seguente

in cui ΔU(T′) è il calore di reazione a volume costante e alla temperatura T′. Quindi è possibile calcolare la variazione di energia libera ΔF=ΔU−TΔS, che determina la possibilità che la reazione avvenga alla temperatura data, se si conosce il calore di reazione (a volume costante) per tutte le temperature inferiori. Nernst scrisse che lo scopo principale della termochimica, ossia il calcolo esatto dell'equilibrio chimico a partire dai calori di reazione, appare ora accessibile.

Un ultimo gruppo di applicazioni della termodinamica del XIX sec. riguarda il calore radiante o la luce. Nel 1859 confrontando le linee scure dello spettro solare con lo spettro di emissione del sodio, Gustav Robert Kirchhoff (1824-1887) stabilì un legame teorico tra il potere di assorbimento e il potere di emissione della luce, o del calore radiante, in una sostanza. Il suo ragionamento si basava sull'applicazione dei principî della termodinamica a un apparato immaginario: due piastre poste l'una di fronte all'altra, ognuna con la faccia esterna coperta da uno specchio. Per ciascuna delle piastre, il primo principio della termodinamica implica che il bilancio tra la radiazione emessa e quella assorbita debba fornire il calore sviluppato nella piastra. Il secondo principio, nella formulazione di Clausius, stabilisce che le due piastre debbano restare alla stessa temperatura, se lo sono all'inizio. Per ogni piastra, quindi, la radiazione totale emessa deve uguagliare quella totale assorbita. Applicando questa condizione al caso in cui una delle piastre assorbe ed emette radiazione a una sola lunghezza d'onda, Kirchhoff dimostrò che il rapporto tra il potere emissivo e quello assorbente era una funzione universale della lunghezza d'onda, indipendente dalla sostanza considerata. L'anno seguente ricavò nuovamente la stessa conclusione attraverso un altro 'esperimento mentale', che richiedeva l'esistenza di un 'corpo nero', completamente assorbente a tutte le lunghezze d'onda, e di filtri con profili di assorbimento variabili.

Mentre Kirchhoff usò il secondo principio di Clausius per vincolare la forma delle leggi della radiazione, altri utilizzarono tali leggi per tentare di violare il secondo principio di Clausius. Nel 1852 Rankine avanzò l'ipotesi che il calore radiante dell'Universo potesse essere riflesso ai confini di questo e rifocalizzato in punti specifici come il Sistema solare, sperando così di scongiurare la morte termica di Thomson. Nel 1863 Clausius dimostrò che le quantità di calore scambiate attraverso la radiazione da due elementi di superficie alla stessa temperatura erano sempre in equilibrio se valeva la legge di Kirchhoff, qualsiasi dispositivo ottico si frapponesse tra gli elementi stessi. Ne concluse che ogni tentativo di violare il suo secondo principio attraverso processi radiativi era destinato a fallire.

Gli esperimenti mentali sulla radiazione di Kirchhoff e di Clausius si limitavano a sistemi statici composti da corpi riscaldati, specchi e filtri. Nel 1876, il fisico italiano Adolfo Bartoli (1851-1896) concepì un ingegnoso ciclo a quattro fasi, in cui si utilizzava un movimento di specchi per trasferire radiazione termica da un corpo nero più freddo a uno più caldo. Per evitare questa violazione del secondo principio di Clausius, egli ipotizzò che la radiazione esercitasse una pressione sugli specchi e che il lavoro corrispondente giustificasse il trasferimento di calore. Fonti di ispirazione di Bartoli furono il 'radiometro' di William Crookes del 1875 e la sua interpretazione, presto dimostratasi errata, nei termini della pressione di radiazione di Maxwell. Nel 1884 il fisico americano Henry T. Eddy propose un esperimento mentale simile, con l'intento di confutare il secondo principio di Clausius e la morte termica dell'Universo. Ne seguì una polemica, che spinse Bartoli a ripubblicare le sue considerazioni nel "Nuovo Cimento". Ludwig Boltzmann presto corresse la stima di Bartoli della pressione di radiazione e dimostrò che la legge sperimentale di Joseph Stefan, E=σT⁴ (dove σ è la costante di Stefan), per il potere emissivo totale di un corpo nero, derivava dal secondo principio e dalla formula di Maxwell per la pressione di radiazione.

Quest'ultima dimostrazione di Boltzmann si basava su una versione perfezionata dell'esperimento mentale di Bartoli. Nel 1893 Wilhelm Wien utilizzò lo stesso tipo di esperimento concettuale allo scopo di mettere in relazione lo spettro di corpo nero a una determinata temperatura con lo spettro di corpo nero a un'altra temperatura. L'idea di base era che lo spostamento di un pistone mobile con la superficie riflettente di uno specchio alterava la lunghezza d'onda della radiazione riflessa a causa dell'effetto Doppler, preservando d'altra parte l'equilibrio termico della radiazione. La forma risultante, u_ν=ν³ f(ν/T), della densità spettrale u_ν alla frequenza ν e alla temperatura T, viene chiamata 'legge dello spostamento di Wien', e giocò un ruolo rilevante nella storia successiva degli studi sulla radiazione di corpo nero, da cui emersero i primi concetti quantistici.

Da questo breve riassunto delle prime considerazioni termodinamiche sulla radiazione, appare chiaro che alla fine dell'Ottocento non vi era un consenso unanime sul grado di generalità da attribuire ai principî della termodinamica. Thomson, Clausius e Planck erano convinti che fossero così generali da potersi applicare anche su scala cosmica; altri ritenevano invece che essi fallissero a causa di alcuni processi radiativi; altri ancora, tra cui Maxwell, Boltzmann e Gibbs, pensavano che il secondo principio avesse soltanto una validità statistica. Infine, la scoperta della radioattività indusse a formulare congetture su una possibile violazione del principio di conservazione dell'energia. Agli inizi del XX sec. la termodinamica era ormai una teoria relativamente ben compresa, aveva principî enunciati con chiarezza e regole univoche di applicazione; ciononostante, la natura profonda dei suoi principî rimaneva ancora controversa.

Bibliografia

Barkan 1999: Barkan, Diana, Walther Nernst and the transition to modern physical science, Cambridge-New York, Cambridge University Press, 1999.

Bevilacqua 1993: Bevilacqua, Fabio, Helmholtz's Über die Erhaltung der Kraft. The emergence of a theoretical physicist, in: Hermann von Helmholtz and the foundations of nineteenth-century science, edited by David Cahan, Berkeley, University of California Press, 1993, pp. 291-333.

Brush 1976: Brush, Stephen G., The kind of motion we call heat. A history of the kinetic theory of gases in the 19th century, Amsterdam, North Holland, 1976, 2 v.

Caneva 1993: Caneva, Kenneth L., Robert Mayer and the conservation of energy, Princeton, Princeton University Press, 1993.

Cardwell 1971: Cardwell, Donald S.L., From Watt to Clausius. The rise of thermodynamics in the early industrial age, Ithaca (N.Y.), Cornell University Press, 1971 (rist.: Ames, Iowa State University Press, 1989).

Chang 2001: Chang, Hasok, Spirit, air, and quicksilver. The search for the 'real' scale of temperature, "Historical studies in the physical and biological sciences", 31, 2001, pp. 249-284.

Costabel 1960: Costabel, Pierre, Leibniz et la dynamique. Les textes de 1692, Paris, Hermann, 1960 (ediz. bilingue: Leibniz et la dynamique. Les textes de 1692. Leibniz and dynamics. The texts of 1692, Paris, Hermann; Ithaca (N.Y.), Cornell University Press, 1973).

Darrigol 1992: Darrigol, Olivier, From c-numbers to q-numbers. The classical analogy in the history of quantum theory, Berkeley, University of California Press, 1992.

‒ 2001: Darrigol, Olivier, God, waterwheels, and molecules. Saint-Venant's anticipation of energy conservation, "Historical studies in the physical and biological sciences", 31, 2001, pp. 285-353.

Daub 1971: Daub, Edward E., Clausius, Rudolf, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner's Sons, 1970-1990, 18 v.; v. III, 1971, pp. 303-311.

Dolby 1984: Dolby, Riki G.A., Thermochemistry versus thermodynamics. The nineteenth century controversy, "History of science", 22, 1984, pp. 375-400.

Dörries 1998: Dörries, Matthias, Vicious circles, or the pitfalls of experimental virtuosity, in: Experimental essays. Versuche zum Experiment, hrsg. von Michael Heidelberger und Friedrich Steinle, Baden-Baden, Nomos, 1998, pp. 123-140.

Fox 1971: Fox, Robert, The caloric theory of gases. From Lavoisier to Regnault, Oxford, Clarendon, 1971.

Grattan-Guinness 1984: Grattan-Guinness, Ivor, Work for the workers. Advances in engineering mechanics and instruction in France, 1800-1830, "Annals of science", 41, 1984, pp. 1-33.

Harman 1982: Harman, Peter M., Energy, force, and matter. The conceptual development of nineteenth century physics, Cambridge-New York, Cambridge University Press, 1982.

Hiebert 1978: Hiebert, Erwin N., Nernst, Hermann Walther, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner's Sons, 1970-1990, 18 v.; v. XIV, 1978, pp. 432-453.

Hong 1994: Hong, Sungook, Controversy over voltaic contact phenomena. 1862-1900, "Archive for history of exact sciences", 47, 1994, pp. 233-289.

Klein 1969: Klein, Martin J., Gibbs on Clausius, "Historical studies in physical and biological sciences", 1, 1969, pp. 127-149.

‒ 1972: Klein, Martin J., Gibbs, Josiah Willard, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner's Sons, 1970-1990, 18 v.; v. V, 1972, pp. 386-393.

Kragh 1984: Kragh, Helge, Julius Thomsen and classical thermochemistry, "British journal for the history of science", 17, 1984, pp. 255-272.

‒ 1989: Kragh, Helge - Carazza, Bruno, Adolfo Bartoli and the problem of radiant heat, "Annals of science", 46, 1989, pp. 183-194.

‒ 1993: Kragh, Helge, Between physics and chemistry. Helmholtz's route to a theory of chemical thermodynamics, in: Hermann von Helmholtz and the foundations of nineteenth-century science, edited by David Cahan, Berkeley, University of California Press, 1993, pp. 403-431.

Kuhn 1959: Kuhn, Thomas S., Energy conservation as an example of simultaneous discovery, in: Critical problems in the history of science, edited by Marshall Clagett, Madison, University of Wisconsin Press, 1959, pp. 321-356.

Sibum 1995: Sibum, Otto, Reworking the mechanical value of heat: Instruments of precision and gestures of accuracy in early Victorian England, "Studies in the history and philosophy of science", 26, 1995, pp. 273313.

Siegel 1976: Siegel, Daniel, Balfour Steward and Gustav Robert Kirchhoff. Two independent approaches to 'Kirchhoff's radiation law', "Isis", 67, 1976, pp. 565-600.

Smith 1989: Smith, Crosbie - Wise, M. Norton, Energy and empire. A biographical study of Lord Kelvin, Cambridge, Cambridge University Press, 1989.

‒ 1998: Smith, Crosbie, The science of energy. A cultural history of energy physics in Victorian Britain, Chicago, University of Chicago Press, 1998.

Truesdell 1980: Truesdell, Clifford A., The tragicomical history of thermodynamics. 1822-1854, New York-Berlin, Springer, 1980.