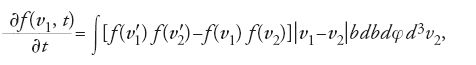L'Ottocento: fisica. La nascita della meccanica statistica

L'Ottocento: fisica. La nascita della meccanica statistica

La nascita della meccanica statistica

Modelli meccanici dei fenomeni termici

Con la locuzione 'meccanica statistica' il fisico americano Josiah W. Gibbs (1839-1903) designa lo studio delle proprietà statistiche di un grande numero di sistemi meccanici della stessa natura. In questo capitolo la storia della meccanica statistica verrà delineata in un senso più ampio; si illustreranno infatti anche i tentativi di spiegare le proprietà termodinamiche dei corpi macroscopici in termini di regolarità statistiche che caratterizzano sistemi composti da numerosi costituenti identici.

Nella seconda metà del XIX sec. la meccanica statistica emerge in un contesto contraddistinto dagli sforzi compiuti per interpretare i fenomeni termici basandosi sulla meccanica, allora considerata il settore fondamentale delle scienze fisiche. Anche se fenomeni come quelli ottici, elettrici, magnetici e termici non erano a prima vista di natura meccanica, gli scienziati cercavano di spiegarli facendo riferimento a entità meccaniche non osservabili quali l'etere o corpuscoli molto piccoli. I modelli meccanici dei fenomeni termici fanno parte della fisica intuitiva ed erano stati utilizzati sin dall'Antichità. La diffusione del calore da un corpo a un altro diveniva così comprensibile come movimento di particelle invisibili oppure come flusso di un fluido invisibile, o anche come effetto di una propagazione ondulatoria. Queste spiegazioni meccaniche del calore potevano anche dar conto dei suoi legami con effetti meccanici percepibili, per esempio la dilatazione termica dei corpi, la pressione esercitata dai gas o la possibilità di generare calore dal movimento. Quale di questi modelli meccanici apparisse, in un dato momento storico, il più adatto per la spiegazione del calore dipendeva da molteplici fattori, come la conoscenza disponibile dei fenomeni termici, la sua collocazione nel complesso della fisica e il suo livello di elaborazione.

Il calore come fluido e come movimento

Nel XVIII sec. si sviluppò una concezione in base alla quale il calore veniva considerato un fluido ‒ il cosiddetto 'calorico' ‒ in analogia con le idee contemporanee sulla natura dell'elettricità. Il calore e l'elettricità, in effetti, condividevano molte proprietà che portavano a interpretarne il comportamento in termini di fluidi imponderabili. Per esempio, entrambi non avevano una forma definita, come fu dimostrato dagli esperimenti di calorimetria: il calore poteva essere 'immagazzinato', proprio come l'elettricità, in 'recipienti' appropriati e poteva 'fluire' da un corpo a un altro; entrambi tendevano a diffondersi e a riempire i loro recipienti il più possibile; entrambi erano imponderabili, ossia non avevano un peso apprezzabile. Il modello a fluido spiegava anche il ruolo giocato dal calore nelle reazioni chimiche: il calorico si comportava in modo analogo alle altre sostanze, potendo esistere o allo stato libero o a quello combinato. Alla fine del Settecento il modello a fluido fu inserito nel programma laplaciano di riduzione della fisica all'azione reciproca di forze centrali agenti tra sostanze ponderabili e imponderabili. Più tardi, nelle riflessioni di Sadi Carnot del 1824, esso fu posto alla base della discussione sui limiti teorici delle macchine termiche.

Nel corso della prima metà del XIX sec., diverse acquisizioni contribuirono al graduale abbandono del modello a fluido e alla diffusa accettazione della concezione del calore come forma di movimento. La prima acquisizione fu costituita dal successo ottenuto negli anni Venti dalla teoria ondulatoria della luce a causa della stretta connessione che si supponeva esistesse tra quest'ultima e il calore. Successivamente, negli anni Trenta, fisici italiani come Macedonio Melloni rafforzarono l'analogia tra calore e luce, rivelando tra l'altro l'esistenza di fenomeni di riflessione e rifrazione del calore. La terza acquisizione fu la dimostrazione della possibilità di convertire il lavoro meccanico in calore a seguito degli accurati esperimenti eseguiti da James P. Joule negli anni Quaranta. A partire dal 1850, il modello del calore come forma di movimento fu associato al principio di conservazione dell'energia, che era stato proposto in modo autorevole da William Thomson (lord Kelvin) e Hermann von Helmholtz.

Le idee su quale fosse il tipo di movimento in cui consisteva realmente il calore variavano in maniera considerevole. All'inizio, la concezione più comune era quella, suggerita da André-Marie Ampère, di un moto vibratorio delle molecole che veniva trasmesso dall'etere. Tuttavia questa concezione, anche se spiegava sia il calore radiante sia la conduzione del calore nella materia, era assai meno efficace per quanto riguardava il comportamento dei gas. Alla metà del secolo, autorevoli fisici britannici, tra i quali Thomson, James C. Maxwell e William Rankine, pensarono a moti vorticosi delle molecole dei gas, in lontana analogia con la vecchia spiegazione newtoniana della pressione dei gas come repulsione tra molecole contigue (considerate in stato di quiete). In questa immagine teorica il calore corrispondeva alla rotazione delle molecole e l'elasticità alla loro forza centrifuga.

La teoria cinetica

Sempre nello stesso periodo, Joule, Rudolf Clausius e altri elaborarono una diversa concezione del calore che si basava sul moto traslatorio delle molecole. Essi supponevano che le molecole del gas occupassero solamente una piccola frazione del volume a disposizione e si muovessero di moto rettilineo e uniforme, soltanto occasionalmente interrotto da collisioni con altre molecole oppure con le pareti del recipiente. Anche se questo modello affondava le proprie radici nell'atomismo antico, la sua applicazione ai gas risaliva al XVIII secolo. La prima spiegazione della pressione dei gas basata su di esso fu data da Daniel Bernoulli nel 1738, John Herapath lo aveva riscoperto nel 1820 e venne in seguito riproposto ancora una volta da John Waterston negli anni Quaranta. Semplificando, si assume che la pressione del gas sia proporzionale al numero delle collisioni delle particelle del gas con la parete e alla loro quantità di moto. Essendo, poi, il numero degli urti proporzionale alla densità del gas e alla velocità delle molecole, la pressione risulta proporzionale sia alla densità del gas, in accordo con la legge di Boyle, sia al quadrato della velocità delle molecole, in accordo con la legge di Gay-Lussac, se si suppone che la temperatura sia una funzione lineare del quadrato della velocità.

All'inizio il campo di applicazione di un simile modello era molto limitato. Tuttavia, a differenza del modello a fluido, esso spiegava la conversione tra calore e lavoro meccanico, consentendo nello stesso tempo, a differenza dei modelli vibratori e rotatori, di dare una descrizione quantitativa del comportamento dei gas.

La teoria dei gas tra meccanica e termodinamica

La formulazione della termodinamica, tra il 1840 e il 1850, da parte di Rankine, Thomson e Clausius condusse a una teoria che non era più basata su un modello meccanico. Il primo e il secondo principio di questa teoria trattavano i fenomeni termici esclusivamente in termini di macchine termiche, senza fare riferimento a una sostanza del calore o a un movimento termico. Tuttavia, nel contesto della termodinamica, il modello del calore come forma di movimento acquistava una nuova rilevanza e un nuovo status epistemologico. Mentre prima era servito soltanto alla modellizzazione del comportamento termico dei gas, ora il modello aveva una funzione di collegamento tra due pilastri fondamentali della fisica. Esso rendeva plausibili i processi di conversione tra energia meccanica e termica nelle macchine termodinamiche e quindi forniva un sostegno meccanico alla nuova termodinamica. Inoltre, il supporto così ottenuto ebbe ripercussioni sulla meccanica stessa, che allora era ancora considerata la base concettuale di tutta la fisica. La teoria cinetica dei gas tradusse i progressi della termodinamica in altrettante sfide per la meccanica che alla fine portarono alla creazione della meccanica statistica.

In particolare, lo studio della teoria cinetica consentì agli scienziati di confrontarsi con una delle principali caratteristiche strutturali della termodinamica che la rendono diversa dalla meccanica, ossia l'irreversibilità delle sue leggi rispetto all'inversione del tempo. Quando, per esempio, due parti a diversa temperatura di un liquido sono mescolate tra loro, l'intero liquido raggiungerà una temperatura intermedia; questo processo non è reversibile, ossia il liquido non si separerà mai spontaneamente in una parte più calda e una più fredda. Contrariamente ai processi descritti dalla termodinamica, le leggi della meccanica non sono influenzate da un'inversione della direzione del tempo. Questa contraddizione divenne una sfida per lo sviluppo della teoria cinetica, così come il problema di descrivere sempre più adeguatamente le proprietà di sistemi fisici specifici.

Il fisico che di fatto resuscitò la teoria cinetica dei gas fu Clausius, uno dei fondatori della termodinamica. Nel 1857, egli diede alla relazione di Bernoulli la forma corretta PV= =(1/3)Nmu², dove P è la pressione, V è il volume del recipiente, N il numero delle molecole, m la loro massa e u² il valore medio del quadrato delle loro velocità. In base a questa espressione egli trasse la conclusione che, una volta ammessa l'ipotesi di Avogadro (secondo cui il numero di molecole in un'unità di volume è lo stesso per tutti i gas a condizioni normali), l'energia media dei moti traslatori delle molecole era la stessa per ogni gas. Inoltre egli considerò l'energia interna del gas come l'energia totale dei moti traslatori delle molecole. Da ciò derivava che il calore specifico a volume costante era pari alla costante R dei gas perfetti moltiplicata per 3. Dato che questo valore era molto inferiore a quelli osservati, Clausius concluse che le molecole avevano, oltre ai moti traslatori, anche moti rotatori e vibratori. Le collisioni reciproche facevano sì che le energie medie di questi tre tipi di moto stessero tra loro in rapporti costanti.

Anche se era consapevole del fatto che in seguito alle collisioni le velocità delle molecole assumevano diversi valori, per semplificare i suoi calcoli Clausius suppose che tutte le molecole avessero la stessa velocità. L'approccio del suo primo articolo, über die Art der Bewegung, welche wir Wärme nennen (Sulla natura del movimento che chiamiamo calore, 1857), consisteva nell'eguagliare le proprietà dell'intero sistema con quelle delle singole particelle. Per esempio, egli identificava la temperatura del gas con l'energia cinetica delle sue molecole. Le considerazioni statistiche, che potevano riguardare la formazione dei valori medi, giocavano nelle sue argomentazioni un ruolo marginale. Le ipotesi di Clausius consistevano semplicemente nell'assumere che le molecole occupassero una frazione trascurabile del volume del gas e che esse si muovessero in linea retta con la stessa velocità fino a urtare una delle pareti del recipiente; i dettagli dei processi di collisione reciproca e le forze molecolari non venivano invece presi in considerazione. Tuttavia, l'identificazione diretta delle proprietà del sistema con quelle dei suoi costituenti avrebbe ben presto reso evidente il contrasto tra il suo modello e le conoscenze empiriche sui gas.

Le proprietà di trasporto dei gas

Il problema che portò a concepire i gas come insiemi statistici fu quello relativo alle loro proprietà di trasporto. Uno dei lettori di Clausius, il meteorologo olandese Christoph Hendrik Diederik Buys-Ballot (1817-1890), sollevò l'obiezione che la teoria cinetica implicasse per la diffusione dei gas una velocità molto più alta di quella osservata, dato che le velocità molecolari calcolate da Clausius erano, in condizioni normali, confrontabili con la velocità del suono. Per replicare, Clausius nel 1858 introdusse nell'articolo über die mittlere Länge der Wege (Sulla lunghezza media delle traiettorie) quello che può essere considerato il primo concetto statistico non banale della teoria cinetica, ossia il 'cammino libero medio'. Tale concetto, infatti, non si riferisce né a una proprietà di una particella individuale né a una proprietà di un gas come sistema macroscopico; ha senso solo se il gas viene concepito come un complesso statistico.

Il cammino libero medio è definito come la distanza media percorsa da una molecola prima della collisione con un'altra molecola. Secondo l'argomentazione di Clausius, la frazione di molecole che viaggiando nella direzione dell'asse x e percorrendo la distanza dx urtano un'altra molecola è data dalla frazione πr²ndx della superficie attraversata occupata dalle 'sfere d'azione' delle molecole, dove r è il raggio di azione e n il numero di molecole nell'unità di volume. Ne deriva che la probabilità W(x) che il moto di una molecola rimanga 'libero' per una distanza x è e^−αx, con α=πr²n, mentre la probabilità che questa molecola subisca la sua prima collisione tra x e x+dx è W(x)−W(x+dx)=αe^−αxdx. In base a quest'ultima legge probabilistica, il cammino libero medio l è la media 1/α della distanza x. Clausius prevedeva che questa distanza fosse abbastanza piccola da impedire la diffusione ultrarapida di cui parlava Buys-Ballot.

Partendo dai lavori di Clausius, Maxwell diede un notevole sviluppo agli aspetti statistici della teoria cinetica dei gas. In particolare egli si occupò delle variazioni di velocità prodotte dalle collisioni reciproche tra le molecole. Nel 1860, nell'articolo Illustrations of the dynamical theory of gases, egli determinò la distribuzione di equilibrio f(v) delle velocità molecolari ipotizzando la sua isotropia assieme all'indipendenza statistica delle tre componenti della velocità lungo gli assi delle coordinate. Queste due condizioni portavano alle equazioni funzionali f(v)=φ(v²)=ψ(v_x)ψ(v_y)ψ(v_z), la cui soluzione aveva la forma f(v)=αe^−βv2 dove α e β sono due costanti. Più tardi Maxwell avrebbe giudicato 'precaria' questa dimostrazione, dato che la seconda assunzione non aveva ancora alcuna giustificazione. Tuttavia, egli non avrebbe mai dubitato della validità della funzione di distribuzione delle velocità che oggi porta il suo nome.

Lo scopo principale che Maxwell si era prefisso nell'articolo del 1860 era quello di ricavare nuove conseguenze fisiche dal concetto di cammino libero medio, adottando il modello di un gas composto da un grande numero di sfere perfettamente elastiche. In questo modo egli calcolò l'interdiffusione dei gas e anche l'attrito interno (la viscosità) e la conduzione termica considerati in termini di diffusione della quantità di moto e dell'energia cinetica. In base al ragionamento di Maxwell, le molecole che si allontanano da un dato strato di gas trasportano con sé la loro massa n, la loro quantità di moto e la loro energia cinetica per una distanza dell'ordine del cammino libero medio l, dopo di che trasmettono queste grandezze, mediante gli urti, a un altro strato di gas. Il flusso netto di queste grandezze nella direzione dell'asse x è dell'ordine di lu∂(nq)/∂x, dove q sta rispettivamente per m, mu, (1/2)mu². I coefficienti corrispondenti di diffusione, viscosità e conduzione termica sono dunque rispettivamente lu, nmlu e (P/T)lu con coefficienti numerici che Maxwell ottenne effettuando le medie necessarie sul cammino libero. I valori ottenuti da George G. Stokes (1819-1903) per la viscosità dell'aria e da Thomas Graham (1805-1869) per il coefficiente di interdiffusione di due gas fornivano stime compatibili per il cammino libero medio, valutato dell'ordine di circa 10⁻⁷m (non si avevano invece dati sulla conducibilità termica). Naturalmente questa convergenza giocò a favore dell'approccio maxwelliano.

L'interpretazione della viscosità proposta da Maxwell aveva però una conseguenza meno desiderabile. Dal momento che il cammino libero medio è inversamente proporzionale alla densità del gas, l'attrito interno risulta indipendente dalla densità stessa, con un esito contrario all'intuizione che lasciò perplesso Maxwell. Questa e altre conseguenze non accettabili lo spinsero a dubitare subito della validità complessiva della teoria cinetica. Tuttavia, nel 1866, alcuni esperimenti accuratamente condotti da lui e da sua moglie confermarono la sorprendente indipendenza della viscosità dalla densità: questa importantissima scoperta conferì dunque molta credibilità alla teoria cinetica in generale.

Nello stesso tempo, gli esperimenti di Maxwell erano in contraddizione con il più specifico modello delle sfere rigide; infatti i valori misurati della viscosità risultavano proporzionali alla temperatura assoluta, laddove il modello a sfere rigide prevedeva una proporzionalità rispetto alla radice quadrata della temperatura. Per superare questa difficoltà Maxwell si orientò verso un modello diverso, conservando le ipotesi generali di Clausius ma sostituendo le sfere rigide del 1860 con centri di forza repulsiva. Inoltre egli abbandonò il metodo basato sul cammino libero medio e adottò un approccio più potente ai fenomeni di trasporto, basato sul calcolo del numero delle collisioni di diverse specie di molecole e sulle conseguenti variazioni delle proprietà molecolari medie. L'integrazione delle equazioni che ne risultavano richiedeva la conoscenza della funzione di distribuzione delle velocità in condizioni perturbate, eccetto che nel caso di una forza di interazione tra le molecole inversamente proporzionale alla quinta potenza della distanza. Per questo caso particolare Maxwell determinò il trasporto della massa, della quantità di moto e dell'energia cinetica nel gas. Ritrovò così l'equazione di Navier-Stokes per il moto di gas viscosi e ottenne relazioni quantitative tra viscosità, velocità di diffusione e conducibilità termica. La viscosità risultava proporzionale alla temperatura, in accordo con i suoi esperimenti. Maxwell accolse dunque con sollievo il fatto che la Natura sembrasse aver scelto il caso matematicamente favorevole di forze molecolari variabili secondo la legge 1/r⁵. Egli, tuttavia, era consapevole che questa legge non poteva valere per distanze intermolecolari più grandi, per le quali la forza doveva essere attrattiva, né per distanze tanto piccole da far entrare in gioco la struttura delle molecole.

Pochi anni più tardi, le accurate misurazioni di viscosità dei gas di Oskar Emil Meyer e di Josef Stefan indicarono una dipendenza della viscosità dalla temperatura che non si accordava né con la legge 1/r⁵ né con il modello a sfere rigide. Nel corso degli anni Ottanta i successori di Maxwell lavorarono vanamente sui suoi coefficienti di trasporto. Da un punto di vista retrospettivo si può dire che il problema non avrebbe potuto comunque essere risolto con le tecniche matematiche e i modelli di cui essi disponevano.

La legge di Maxwell-Boltzmann

L'elemento cruciale per la comprensione dei gas intesi come insiemi statistici di particelle era la distribuzione di equilibrio delle velocità. Per questo motivo Maxwell e il suo più importante successore, Ludwig Boltzmann (1844-1906), cercarono di stabilire tale distribuzione con la maggiore certezza possibile, generalizzandola anche a gradi di libertà diversi da quelli traslazionali. Nel 1867 Maxwell ne diede una dimostrazione inedita, servendosi dell'approccio, prima citato, basato sul calcolo del numero delle collisioni tra le molecole. In un contesto viennese favorevole ai metodi atomistici e britannici, Boltzmann restò ovviamente affascinato dalla memoria di Maxwell sulla teoria dinamica dei gas del 1867. Nel 1868 e nel 1871 egli generalizzò l'approccio basato sul numero di collisioni a molecole aventi gradi interni di libertà e soggette a forze esterne come, per esempio, la forza di gravità. Egli arrivò così alla forma αe^−βE per la distribuzione stazionaria delle variabili molecolari dalle quali dipende l'energia E di una molecola. Questa legge, oggi chiamata 'distribuzione di Maxwell-Boltzmann', fa tuttora parte della fisica statistica come elemento essenziale.

Il problema dei calori specifici

La teoria cinetica rese possibile calcolare i calori specifici dei gas a partire dalla distribuzione dell'energia sui diversi gradi di libertà. La soluzione di Maxwell e di Boltzmann a questo problema era basata sul teorema di equipartizione. Nella sua forma più generale, questo teorema stabilisce che a ciascun termine quadratico che compare nell'espressione dell'energia corrisponde un'energia media pari a (1/2)kT, dove k è la costante di Boltzmann e T la temperatura. In particolare, dall'equipartizione conseguono i risultati che Clausius aveva già ottenuto nel 1857, ossia che, per un gas monoatomico a bassa densità composto di N particelle puntiformi, l'energia totale sarebbe stata U=(3/2)NkT e il calore specifico a volume costante C_V=(3/2)Nk.

Nel 1860 Maxwell, con il suo modello a sfere rigide, aveva dimostrato, in base all'ipotesi del carattere casuale delle collisioni tra le molecole del gas, che le collisioni tra due diversi tipi di molecole avrebbero portato progressivamente a rendere uguali le loro energie cinetiche; ciò implicava la validità dell'ipotesi di Avogadro (se si segue il ragionamento di Clausius). Maxwell dimostrò anche che, nel caso di molecole asferiche, rigide ed elastiche, le collisioni producono moti rotatori che hanno un'energia cinetica media uguale a quella dei moti traslatori. Con suo disappunto, il calore specifico risultante era molto più alto di quello osservato per la maggioranza dei gas.

In seguito Maxwell si convinse del fatto che i calori specifici osservati non potevano essere previsti da alcun modello meccanico coerente. Le molecole puntiformi davano un valore troppo piccolo, quelle assimilate a corpi rigidi valori troppo grandi. Per le molecole dei gas poliatomici, che Boltzmann trattò nel 1871, la legge di Maxwell-Boltzmann prevede un'energia media pari a (1/2)kT per ciascun termine quadratico dell'energia della molecola. Come Maxwell dedusse nello scritto del 1875 On the dynamical evidence of the molecular constitution of bodies, ciò implica che il rapporto γ tra i calori specifici a pressione e a volume costante sia pari a 1+2/r, dove r è il numero dei termini quadratici di cui sopra. Se si tiene conto dei gradi di libertà rotazionali e traslazionali, il valore risultante di γ differisce molto da quello osservato sperimentalmente. Il commento di Maxwell fu che ci si trovava di fronte alla più seria difficoltà che la teoria molecolare avesse mai incontrato; alla fine del secolo i fisici non si erano ancora messi d'accordo sulla sua gravità: la soluzione, infatti, avrebbe richiesto l'applicazione della teoria quantistica.

L'equazione di Boltzmann e il teorema H

Tav. I

Fino al 1871 Boltzmann aveva dimostrato la stazionarietà della legge di Maxwell-Boltzmann, ma non la sua unicità. Nel 1872, per colmare questa lacuna, in uno scritto intitolato Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen (Altri studi sull'equilibrio termico fra molecole di gas), egli ricostruì l'evoluzione della distribuzione di velocità dei gas a partire da uno stato iniziale qualsiasi fino all'equilibrio. Secondo il suo ragionamento, se il numero di collisioni che si verificano in un gas distribuito spazialmente in modo omogeneo è noto, allora l'evoluzione della distribuzione delle velocità può essere calcolata. La variazione, in un dato intervallo di tempo δt, del numero di molecole con velocità v₁, in un intervallo pari a d³v₁, è uguale al numero di collisioni tale per cui la velocità finale di una delle molecole appartiene al suddetto intervallo di velocità, meno il numero di collisioni tale per cui la velocità iniziale di una molecola appartiene a quell'intervallo. Utilizzando le formule di Maxwell per il numero delle collisioni dirette e inverse (Tav. I) e tenendo conto del fatto che la velocità relativa e il prodotto d³v₁d³v₂ restano invariati durante una collisione, si ottiene il caso più semplice della cosiddetta 'equazione di Boltzmann':

dove v′₁ e v′₂ sono le velocità finali di due molecole che prima della collisione avevano velocità v₁ e v₂, b è il parametro d'urto e φ l'angolo azimutale. Questa equazione determina completamente l'evoluzione di f a partire dal suo stato iniziale. Essa implica la stazionarietà della distribuzione maxwelliana, dato che l'annullamento della differenza tra le parentesi quadre equivale alla condizione di stazionarietà di Maxwell.

A questo punto Boltzmann introdusse la funzione

[2]  H=∫flnfd³v,

(originariamente chiamata E, probabilmente perché aveva la stessa forma dell'espressione dell'entropia). Come conseguenza dell'equazione di Boltzmann, questa funzione risulta strettamente decrescente del tempo, a meno che la distribuzione f non sia quella di Maxwell. Ne deriva che quest'ultima è l'unica a essere stazionaria e che ogni altra distribuzione tende a quella di Maxwell. Questo è il contenuto del cosiddetto 'teorema H'. Boltzmann fece anche notare che il valore di −H, corrispondente alla distribuzione maxwelliana, era identico a quello dell'entropia di Clausius. Inoltre, nel caso di distribuzioni diverse da quella maxwelliana, egli propose di considerare tale funzione (−H) come una generalizzazione del concetto di entropia a stati di non-equilibrio, dato che essa era una funzione del tempo sempre crescente. Infine Boltzmann estese la sua equazione a distribuzioni e sistemi di natura più generale.

L'equazione di Boltzmann è diventata uno strumento essenziale per trattare i fenomeni di trasporto nella fisica statistica. Ai tempi di Boltzmann, però, essa poteva essere risolta solo nel caso delle forze dipendenti da 1/r⁵ introdotte da Maxwell, anche se Boltzmann tentò tenacemente di estenderla al modello delle sfere rigide. Solo all'inizio del XX sec. si sarebbero resi disponibili metodi più efficaci, basati sulla teoria delle perturbazioni, per risolvere l'equazione in casi più realistici.

Sfide alla seconda legge

La connessione tra meccanica e termodinamica rappresentata dalla teoria cinetica non ebbe solo ripercussioni sulle concezioni meccaniche, nelle quali venivano introdotti concetti statistici per la descrizione del moto molecolare, ma influenzò anche, in modo analogo, la comprensione della termodinamica. Maxwell riteneva che la teoria cinetico-molecolare mettesse in evidenza i limiti della seconda legge della termodinamica, indicandone il carattere statistico. In una lettera a Peter Guthrie Tait del dicembre 1867 e nel trattato Theory of heat (1871), egli immaginò che "un essere finito", in grado di "vedere le singole molecole", sarebbe stato in grado di creare un flusso di calore da un corpo freddo a uno caldo senza spendere lavoro. Questo essere, che poco tempo dopo Thomson chiamò 'demone di Maxwell', avrebbe in effetti potuto agire su un diaframma, posto su una parete isolante che separava un gas a temperatura più elevata da un gas a temperatura più bassa, in modo da far passare dalla parte fredda alla parte calda solo le molecole più veloci. Nelle discussioni con Thomson e John W. Strutt, Maxwell metteva in relazione questa eccezione alla seconda legge con quella che derivava dall'immaginare un'inversione delle velocità di tutte le molecole a un dato istante. Come egli scriveva a Strutt nel 1870, "la seconda legge della termodinamica ha lo stesso grado di verità dell'affermazione che una volta che hai versato un secchio d'acqua nel mare non puoi più raccogliere di nuovo la stessa acqua" (Maxwell 1990-95, II, pp. 582-583). In seguito Maxwell si espresse in termini di 'certezza statistica' della seconda legge. Nel 1878 nell'articolo Diffusion dell'Encyclopaedia Britannica egli osservò come la dissipazione di lavoro durante l'interdiffusione di due gas dipendeva dalla nostra capacità di separarli fisicamente o chimicamente, concludendo che "la dissipazione dell'energia dipende dai limiti della nostra conoscenza […]. Solo per un essere di scala intermedia, che può controllare alcune forme di energia mentre altre sfuggono alla sua presa, l'energia appare come qualcosa che passa inevitabilmente dallo stato utilizzabile a quello dissipato" (Maxwell 1878b [1990-95, II, p. 646]).

Nel 1871, un anno prima della pubblicazione del teorema H, Boltzmann sottolineò il fatto che l'interpretazione meccanica della seconda legge della termodinamica richiedeva considerazioni probabilistiche. Egli notò anche che, dal punto di vista meccanico, l'energia di un sistema in contatto termico con un termostato fluttuava nel tempo. Ancora prima, nel 1868, negli Studien über das Gleichgewicht der lebendigen Kraft zwischen bewegten materiellen Punkten (Studi sull'equilibrio dell'energia viva fra punti materiali in moto) egli aveva notato che particolari stati iniziali del gas, per esempio quello in cui tutte le molecole giacciono inizialmente sullo stesso piano, non possono raggiungere una situazione di equilibrio. Nell'introduzione della memoria sull'equazione che ha preso il suo nome ‒ Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen ‒, Boltzmann insisteva sul fatto che "i problemi della teoria meccanica del calore [erano] problemi di calcolo delle probabilità" e che la regolarità osservata delle proprietà medie di un gas dipendeva dall'estrema grandezza del numero delle molecole. Tuttavia il suo teorema H veniva enunciato in termini assoluti: H "deve necessariamente diminuire". Nel 1876 il collega viennese di Boltzmann, Joseph Loschmidt, fece notare che non tutti gli stati iniziali del gas soddisfacevano il teorema. In particolare, egli osservava, la reversibilità delle leggi della meccanica aveva come conseguenza il fatto che a ogni evoluzione del sistema che faceva diminuire H doveva corrispondere un'evoluzione inversa per la quale H aumentava. La dimostrazione di Boltzmann della diminuzione di H sembrava quindi essere in contraddizione con le basi meccaniche della teoria.

Boltzmann replicò a questo paradosso con lo scritto Bemerkungen über einige Probleme der mechanischen Wärmetheorie (Osservazioni su alcuni problemi della teoria meccanica del calore, 1877), considerandolo "estremamente pertinente", e adoperando il modello, più intuitivo, della distribuzione spaziale di sfere rigide: "Non è possibile dimostrare che, per ogni possibile posizione e velocità iniziali delle sfere, la loro distribuzione deve diventare più uniforme dopo un tempo molto lungo; si può solo dimostrare che il numero di stati iniziali che portano a uno stato uniforme è infinitamente più grande di quello degli stati iniziali che portano a uno stato non uniforme dopo un lungo intervallo di tempo dato; in quest'ultimo caso la distribuzione tornerà a essere uniforme dopo un tempo ancora più lungo" (Boltzmann 1877a [1909, II, p. 117 e segg.]).

L'intuizione di Boltzmann, espressa nei termini attuali di 'microstato' e 'macrostato', dimostrava che il numero di microstati compatibili con un macrostato uniforme era enormemente più grande di quello compatibile con un macrostato non uniforme. Quindi se ne poteva dedurre che l'evoluzione del gas verso una maggiore uniformità era immensamente più probabile.

L'interpretazione probabilistica dell'entropia

Alla precedente soluzione del paradosso di Loschmidt, Boltzmann, sempre nella stessa memoria, aggiunse la seguente osservazione: "Oltre al numero relativo delle diverse distribuzioni di stato si potrebbe anche calcolare la loro probabilità: il che forse ci condurrebbe a un metodo interessante per la trattazione matematica dell'equilibrio termico" (ibidem, p. 121). Questo è, appunto, ciò che egli riuscì a fare pochi mesi più tardi con il lavoro über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung (Sul rapporto fra il secondo principio della teoria meccanica del calore e il calcolo delle probabilità, 1877). La probabilità che egli aveva in mente era proporzionale al numero di microstati corrispondenti a un dato macrostato. Tale numero era difficile da definire finché si riteneva che la configurazione delle molecole potesse variare con continuità.

La procedura che Boltzmann fu in grado di concepire era legata alla sua particolare visione del concetto di continuità così come l'aveva introdotta nel calcolo. Dal suo punto di vista, infatti, gli integrali e i differenziali erano solo espressioni sintetiche rispettivamente di somme di molti termini e di differenze finite piccole. Oggetti e processi discreti erano più fondamentali e più rigorosamente definibili rispetto a quelli continui. Come era avvenuto, per esempio, nella sua derivazione del teorema H, Boltzmann, quando si trovava di fronte a integrazioni difficili o a equazioni integro-differenziali, analizzava le loro controparti discrete per avere una visione più chiara delle soluzioni possibili.

Dunque Boltzmann cominciò le sue considerazioni sulle probabilità di stato con una 'finzione' matematica: l'energia di una molecola può essere solo un multiplo intero iε di un elemento finito ε. Ne deriva che il microstato, o, secondo Boltzmann, 'complessione', del gas è definito da una serie di N numeri interi che indicano ciascuno il numero di elementi di energia di ogni molecola. Il macrostato, a sua volta, diviene allora la versione discreta della distribuzione dell'energia: per ciascun possibile valore iε dell'energia, esso indica i numeri N_i delle molecole con quella energia. Quindi la probabilità di un dato macrostato è proporzionale alla sua 'permutabilità' N!/(N₁! N₂!… N_i!…). Per un dato valore del numero totale delle molecole ∑N_i e dell'energia ∑N_iiε, usando l'approssimazione di Stirling per i fattoriali, tale permutabilità assume un valore massimo quando N_i è proporzionale a e^−βiε (dove β è il moltiplicatore di Lagrange associato al vincolo dell'energia totale fissata). Dopodiché Boltzmann sostituì la suddivisione uniforme dell'asse dell'energia con una suddivisione uniforme dello spazio delle velocità e calcolò il limite continuo della distribuzione N_i, ottenendo la distribuzione delle velocità di Maxwell. Per una qualsiasi distribuzione N_i, il logaritmo della permutabilità è, nell'approssimazione di Stirling, −∑N_ilnN_i (a meno di una costante), ovvero, nella versione continua, è identico a −H. Ne risulta che la funzione −H, ossia l'entropia del gas, è uguale alla probabilità combinatoria della distribuzione del gas stesso, come Boltzmann aveva già intravisto nella sua replica a Loschmidt.

Nel 1878, nell'articolo über die Beziehung der Diffusionsphänomene zum zweiten Hauptsatze der mechanischen Wärmetheorie (Sul rapporto tra i fenomeni di diffusione e il secondo principio della teoria meccanica del calore), Boltzmann usò l'approccio combinatorio per spiegare l'esistenza di un'entropia di mescolamento per due gas chimicamente equivalenti. Nel 1883, dopo aver letto i lavori di Helmholtz sulla termodinamica dei processi chimici, egli mostrò come il suo metodo combinatorio, applicato a una reazione chimica reversibile, spiegasse la dipendenza dell'equilibrio dall'entropia della reazione. In questo contesto Helmholtz introdusse la distinzione tra 'moto ordinato', che poteva essere convertito completamente in lavoro, e 'moto disordinato', che consentiva solo una conversione parziale. Seguendo questo suggerimento, Boltzmann identificò la permutabilità con la misura del disordine associato a una distribuzione. L'entropia di mescolamento divenne così l'ovvio equivalente dell'aumento di disordine.

La curva H

L'interpretazione probabilistica fornita da Boltzmann per la funzione H non riuscì a tacitare le critiche al teorema H. Nel 1894, i fisici inglesi che si occupavano di teoria cinetica invitarono Boltzmann al congresso annuale della British Association for the Advancement of Science, anche per fare chiarezza sul significato di questo teorema. Uno di essi, Samuel H. Burbury (1831-1911), propose un'innovazione terminologica ‒ il 'caos molecolare' ‒ introdotta per designare una condizione per la validità della formula delle collisioni introdotta da Maxwell. Burbury e lo stesso Boltzmann fornirono anche un'interpretazione intuitiva di questa condizione (che non deve essere tuttavia confusa con il concetto molare di 'disordine' già introdotto da Helmholtz): essa corrisponde all'esclusione di configurazioni predisposte in modo particolare, per esempio quelle in cui le velocità delle molecole più vicine puntano le une verso le altre. Finché il gas resta molecolarmente disordinato la funzione H evolve secondo l'equazione di Boltzmann. Quest'ultimo, peraltro, non escludeva interamente stati ordinati. Egli ammise persino che uno stato inizialmente disordinato avrebbe potuto, di tanto in tanto, passare attraverso stati ordinati con conseguenti fluttuazioni dell'entropia verso valori decrescenti. Tuttavia egli considerava questi eventi occasionali come estremamente improbabili.

A questo punto di vista gli interlocutori inglesi di Boltzmann opposero una versione raffinata del paradosso della reversibilità. Infatti essi osservarono che gli stati corrispondenti a stati crescenti o decrescenti di H in un gas isolato avrebbero dovuto essere ugualmente frequenti, dato che essi si convertono l'uno nell'altro in seguito a un'inversione del tempo. Per chiarire questo punto Boltzmann analizzò la forma della curva H reale determinata dalla dinamica molecolare, discutendone le relazioni con le variazioni di H indicate dall'equazione di Boltzmann. La curva reale, infatti, è l'effetto cumulativo della rapida successione di collisioni che avvengono nel gas; essa, quindi, possiede una forma estremamente irregolare e non ammette una ben definita derivata dH/dt, nel senso ordinario del termine. è chiaro allora che la versione raffinata del paradosso della reversibilità fallisce, dato che essa identifica implicitamente il decremento di H con il segno negativo della sua derivata. Una formulazione rigorosa dell'interpretazione boltzmanniana del decremento di H è la seguente: per un macrostato iniziale fuori dall'equilibrio e per un tempo finito di evoluzione, il numero di microstati compatibili per i quali H diminuisce è molto più grande del numero di microstati compatibili per i quali H aumenta. Questa formulazione è rigorosamente simmetrica rispetto alla direzione del tempo. Essa significa che, considerando un intervallo di tempo molto lungo, H è quasi sempre molto vicina allo zero e che la frequenza delle sue fluttuazioni diminuisce molto rapidamente con la loro ampiezza. Pertanto, come sosterrà Boltzmann nello scritto del 1895, On certain questions of the theory of gases, un qualsiasi valore significativo di H è con grande probabilità molto vicino a un massimo della curva H. A partire da questo punto H può aumentare per un certo tempo, ma tale tempo è con grande probabilità molto piccolo e sarà seguito da una diminuzione per lo più uniforme.

L'anno seguente l'assistente di Max Planck, Ernst Zermelo (1871-1953), formulò un'ulteriore obiezione al teorema H basata sul teorema di ricorrenza di Jules-Henri Poincaré secondo il quale un qualsiasi sistema meccanico (regolato dalle equazioni di Hamilton), che evolve in uno spazio finito con un numero finito di gradi di libertà, torna dopo un tempo sufficientemente lungo arbitrariamente vicino alla sua configurazione iniziale (fatta eccezione per alcuni tipi particolari di moto). Il teorema, secondo Zermelo e Planck, rendeva in linea di principio impossibile la deduzione della legge dell'entropia da un modello meccanico molecolare. Boltzmann, per non protrarre la discussione, replicò che la sua descrizione della curva H era perfettamente compatibile con le suddette ricorrenze, a condizione che il tempo in questione fosse ben oltre il limite dell'umana accessibilità. Con un semplice calcolo egli stimò che il valore del tempo di ricorrenza di un gas era espresso da un numero composto da 10¹⁰ cifre. Egli paragonò Zermelo a un giocatore di dadi che avrebbe dichiarato che un dado era truccato perché non aveva mai ottenuto una sequenza di mille 1.

La prima ricezione della teoria cinetica

L'attacco di Zermelo era un sintomo dell'ostilità di molti fisici verso considerazioni di tipo atomistico. Esponenti illustri della fisica tedesca come Gustav Robert Kirchhoff, Helmholtz e Planck erano a favore di una fisica macroscopica basata su equazioni differenziali che regolavano grandezze osservabili. Spesso le previsioni sperimentali della teoria cinetico-molecolare potevano essere ottenute anche con metodi semplicemente macroscopici. Le uniche eccezioni importanti erano costituite dalla convergenza delle determinazioni del cammino libero medio ottenute dai fenomeni di viscosità, di diffusione e conduzione termica e dalla compatibilità delle stime del numero di Avogadro effettuate da Loschmidt (1865), Thomson (1870) e altri sulla base dei valori del cammino libero medio e di altri fenomeni. Boltzmann avrebbe aggiunto a questi successi la sua spiegazione dei calori specifici dei gas monoatomici e biatomici, in termini di molecole rigide con simmetria sferica e cilindrica. Tuttavia questa era una conclusione controversa. Maxwell stesso pensava che l'elasticità delle molecole di Boltzmann implicasse l'equipartizione dell'energia su tutti i loro gradi di libertà, incluse le vibrazioni interne. In sintesi, i successi sperimentali giustificavano a mala pena le difficoltà matematiche e concettuali della teoria cinetica.

Mentre in Germania i soli ricercatori importanti che lavoravano sulla teoria cinetica e sulle sue conseguenze sperimentali erano Clausius e Meyer, in Gran Bretagna erano impegnati sullo stesso argomento più studiosi, anche per il diffuso entusiasmo verso le teorie dinamiche. Il testo di John Tyndall, Heat as a mode of motion (1862), ebbe un notevole successo e contribuì efficacemente alla divulgazione della teoria cinetica; nel 1876 fu pubblicato il Treatise on the kinetic theory of gases di Henry W. Watson. A partire dal 1890, in Gran Bretagna l'attività di ricerca in questo settore era senza dubbio fiorente. Tuttavia, né in questo paese né in Austria, dove l'interesse tradizionale per le teorie molecolari aveva favorito lo sviluppo delle teorie di Boltzmann e aveva stimolato le importanti ricerche sperimentali di Stefan, la teoria cinetica riuscì a ottenere un chiarimento completo dei propri fondamenti tecnici e concettuali.

I suoi stessi fondatori non erano d'accordo sullo status e sulla portata della loro teoria; essi non proposero una presentazione canonica del suo nucleo fondante che avrebbe potuto contribuire a porre le basi di una tradizione comune. Maxwell non scrisse mai un trattato sulla teoria cinetica; in una lettera a Tait commentava ironicamente gli scritti di Boltzmann nel modo seguente: "Più studio Boltzmann più mi riesce difficile comprenderlo. Così come lui non potrebbe capirmi data la mia stringatezza, per me le sue lungaggini costituiscono un ostacolo insormontabile" (Maxwell 1990-95, II, pp. 915-916). Le Vorlesungen über Gastheorie (Lezioni sulla teoria dei gas) di Boltzmann arrivarono tardi (negli anni 1896-1898), peraltro trattando solo alcuni aspetti del proprio lavoro e di quello di Maxwell. La conseguenza fu che il campo rimase aperto per quelle estensioni e reinterpretazioni che avrebbero portato alla moderna meccanica statistica.

Dalla teoria cinetica alla meccanica statistica

La meccanica statistica fornisce alcuni strumenti per analizzare i processi termici non solo in riferimento ai gas ma anche per sistemi fisici generali con gradi di libertà microscopici, quale che sia la loro esatta costituzione. Al centro della meccanica statistica vi è il concetto di 'insieme virtuale' di sistemi macroscopici, considerati tutti caratterizzati dalla stessa dinamica ma diversi tra loro per la configurazione microscopica iniziale. Invece di ricostruire il comportamento statistico dei costituenti atomici di un sistema macroscopico, la meccanica statistica studia le proprietà di un insieme così definito. Diversi tipi di sistemi termodinamici in equilibrio sono rappresentati da diversi insiemi statistici: in particolare, un sistema isolato dal punto di vista termodinamico è rappresentato da un 'insieme microcanonico', nel quale tutti i membri hanno la stessa energia; un sistema in equilibrio con una sorgente di calore è rappresentato da un 'insieme canonico', in cui le energie dei membri sono distribuite secondo una legge esponenziale. Le proprietà termodinamiche sono quindi ricavate effettuando operazioni di media sull'insieme. Grazie a questo suo carattere generale, la meccanica statistica può essere utilizzata sia in fisica classica, sia ‒ con le opportune modifiche ‒ in fisica quantistica. Ed è per questo motivo che essa poté giocare appunto un ruolo decisivo nella transizione dalla fisica classica alla moderna fisica quantistica.

Di fatto tutti gli elementi fondamentali della meccanica statistica possono essere rintracciati nelle numerose pubblicazioni di Maxwell e di Boltzmann. Tuttavia in queste pubblicazioni tali elementi vengono presentati secondo prospettive diverse rispetto a quelle della meccanica statistica odierna. La prima formulazione autonoma e coerente della meccanica statistica fu proposta da Gibbs nel trattato Elementary principles in statistical mechanics, pubblicato nel 1902. In questo lavoro sono introdotte le locuzioni già viste, oggi abituali, di 'insieme microcanonico' e 'insieme canonico'. Nello stesso anno Albert Einstein pubblicò il primo di una serie di tre articoli che davano, indipendentemente da Gibbs, un'altra formulazione generale della meccanica statistica, Kinetische Theorie des Wärmegleichgewichtes und des zweiten Hauptsatzes der Thermodynamik (Teoria cinetica dell'equilibrio termico e del secondo principio della termodinamica). Questi lavori fornirono le basi per le indagini di Einstein in fisica quantistica, e anche per la sua analisi del moto browniano e di altri fenomeni di fluttuazione come prova sperimentale a favore dell'esistenza degli atomi. Nel medesimo periodo, la stessa teoria cinetica subì ulteriori sviluppi e approfondimenti, sicché all'inizio del XX sec., per la trattazione dei problemi più disparati di fisica statistica, era disponibile una notevole varietà di approcci.

Questo sviluppo dei metodi statistici era stimolato dalla necessità di integrare le crescenti conoscenze sui processi atomici e statistici, come, per esempio, la conduzione ionica ed elettronica e la radiazione termica. L'applicazione a questi nuovi contesti spostò il centro dell'attenzione della teoria cinetica del calore dalle questioni affrontate da Maxwell e Boltzmann e riguardanti i fondamenti meccanici della teoria al problema di trattare sistemi fisici generali in equilibrio termico. In seguito a questo cambiamento di prospettiva, i risultati della teoria cinetica assunsero un nuovo significato, andando a costituire altrettante pietre angolari di una fisica statistica concepita in modo più ampio. In ciò che segue verrà ricostruita sinteticamente la genesi di questo nuovo tipo di fisica, ricapitolando dapprima le sue radici negli 'approcci globali' alla teoria cinetica di Maxwell e di Boltzmann, discutendo poi l'estensione della teoria cinetica a nuovi fenomeni e infine presentando i risultati ottenuti da Gibbs e da Einstein come l'effetto di una riflessione su questi sviluppi.

Gli approcci globali

Nella sua forma originaria più semplice la teoria cinetica si basava sulla statistica molecolare. Boltzmann e Maxwell proposero però anche altri approcci, rivolti alla definizione della probabilità delle configurazioni dell'intero sistema. Mentre l'approccio originario è più intuitivo e porta di per sé allo studio dei processi irreversibili, il secondo fornisce metodi formidabili per ricavare le proprietà di equilibrio di sistemi molto generali. Purtroppo, però, non esiste un percorso univoco e diretto per definire e ricavare queste proprietà globali. Ciò spiega perché le considerazioni pionieristiche di Boltzmann su tali probabilità poterono essere seguite da una varietà di reinterpretazioni, ivi incluse le meccaniche statistiche di Gibbs e di Einstein.

Il primo esempio di approccio globale si trova nella fondamentale, già citata, memoria di Boltzmann del 1868, nella quale egli introdusse la distribuzione ϱ(r₁,r₂,…,r_N; v₁,v₂,…,v_N) per la quale ϱdσ fornisce la frazione di tempo che, dopo un intervallo molto lungo, un sistema di N atomi puntiformi trascorre dentro il volume elementare dσ=d³r₁,d³r₂,…,d³r_N d³v₁, d³v₂,…,d³v_N, nelle vicinanze del punto (r₁,r₂,…,r_N; v₁,v₂,…,v_N) dello spazio delle fasi. Egli, quindi, prese in considerazione l'elemento dσ′ di tale spazio, composto dalle fasi che il sistema assume dopo essersi evoluto, per un tempo costante τ, a partire da una qualsiasi fase di dσ. La frazione di tempo trascorso dal sistema in questi due elementi è ovviamente uguale e quindi: ϱdσ=ϱ′dσ′. Dato che, per il teorema di Liouville (che Boltzmann riscoprì in questa circostanza) dσ=dσ′, e dato che il tempo τ è arbitrario, la distribuzione ϱ è costante lungo la traiettoria del sistema nello spazio delle fasi. Boltzmann credeva inoltre che la traiettoria di sistemi sufficientemente complessi avrebbe riempito il volume dello strato dello spazio delle fasi accessibile al sistema (quello compreso tra le superfici corrispondenti agli estremi dell'intervallo dE di incertezza dell'energia), con l'eccezione di configurazioni particolari altamente instabili ‒ si tratta di quella che più tardi Paul Ehrenfest (1880-1933) avrebbe chiamato 'ipotesi ergodica'. Di conseguenza, la distribuzione ϱ doveva essere la distribuzione uniforme sullo strato corrispondente a un valore costante dell'energia, ossia quella che più tardi Gibbs avrebbe chiamato 'microcanonica'.

Da questa distribuzione, riguardante il sistema nella sua globalità, si può derivare la distribuzione di un qualsiasi sottosistema debolmente accoppiato in senso termico con il resto del sistema, semplicemente integrando sulle variabili della parte complementare del sistema stesso. Quando il sottosistema è relativamente piccolo, la sua funzione di distribuzione risulta proporzionale a e^−βH, dove H è l'energia del sottosistema espressa come funzione della sua fase. Il sistema complementare gioca il ruolo di un termostato, la cui temperatura assoluta è appunto 1/β (a meno di un fattore costante). Boltzmann ottenne questo risultato generale, che corrisponde alla successiva legge di distribuzione canonica di Gibbs, nel 1871 e lo espose nella memoria Einige allgemeine Sätze über Wärmegleichgewicht (Alcuni principî generali sull'equilibrio termico). Essa naturalmente contiene la legge di Maxwell-Boltzmann nel caso particolare in cui il sottosistema si riduca a una singola molecola.

Nello stesso anno Boltzmann pubblicò l'Analytischer Beweis des zweiten Hauptsatzes der mechanischen Wärmetheorie (Dimostrazione analitica del secondo principio della teoria meccanica del calore), basandosi appunto sulla distribuzione canonica di un sistema in contatto con un termostato. La sua idea era quella di identificare l'energia interna del sistema con la media temporale ⟨H> della sua funzione energia H, e il lavoro fornito al sistema nel corso di una variazione infinitesima delle condizioni esterne con la media temporale della variazione corrispondente dell'energia potenziale. Quindi, il calore scambiato con il termostato è δQ=d⟨H> ‒ ⟨dH>, misurato in unità di energia. Le medie sono basate sulla distribuzione e^−βH/Z, dove Z=∫ e^−βH dσ. Si vede subito che il prodotto βδQ costituisce il differenziale di βH+lnZ. In altre parole, esiste una funzione entropia, che Boltzmann riscrisse l'anno seguente come

[3]  S=-∫ϱlnϱdσ.

In questo caso Boltzmann sottolineò la necessità di considerazioni probabilistiche per ricavare un'espressione dell'entropia su base meccanica.

Nonostante questi notevoli risultati, Boltzmann cominciò ben presto a dubitare della validità dell'ipotesi di ergodicità, che era il presupposto della sua dimostrazione. Tornò quindi al suo approccio cinetico-molecolare, che riteneva meglio fondato anche se meno generale. Nel 1879, con il lavoro On Boltzmann's theorem on the average distribution of energy in a system of material points, fu Maxwell a resuscitare l'approccio globale dandogli un ulteriore approfondimento. Mentre Boltzmann aveva sviluppato il suo ragionamento in termini di probabilità temporali riferite a un singolo sistema, Maxwell adottò la cosiddetta 'specificazione statistica', in base alla quale le proprietà di equilibrio di un sistema termodinamico sono da confrontarsi non con quelle di un singolo sistema meccanico, bensì con quelle di un insieme stazionario di sistemi meccanici. Maxwell dimostrò la stazionarietà dell'insieme microcanonico per un qualsiasi sistema che seguisse le equazioni di Hamilton, ricavando, per tale insieme, la distribuzione di Maxwell-Boltzmann e l'equipartizione dell'energia. Tuttavia, egli non spiegò perché gli insiemi stazionari rappresentassero le proprietà termiche dei corpi macroscopici; riteneva che questa proprietà costituisse un'assunzione plausibile, da verificare con l'esperimento e forse, in prospettiva, da giustificare in base all'ipotesi ergodica.

Boltzmann, che apprezzò il contributo di Maxwell, cercò di colmare tale lacuna con un'argomentazione euristica. Egli mise in evidenza che, dal momento che il comportamento temporale medio di un sistema termodinamico non dipende dalla sua iniziale configurazione microscopica, quasi tutti i sistemi di un insieme devono portare alle stesse medie temporali. Quindi, la media temporale di un singolo sistema può essere sostituita con la media d'insieme della media temporale, che è anche la media temporale della media d'insieme. Pertanto, per un insieme stazionario, la media d'insieme deve essere uguale alla media temporale. Anche se in maniera non rigorosa, questa argomentazione giustificava l'uso di insiemi statistici come modelli meccanici della termodinamica; per Boltzmann, tuttavia, restavano aperte altre possibilità per costruire modelli meccanici della termodinamica.

Per esempio, negli anni Ottanta, Boltzmann riprese l'analogia introdotta da Helmholtz tra i cosiddetti 'sistemi meccanici monociclici' e i sistemi termodinamici. Helmholtz non aveva certo cercato di fornire una descrizione realistica dei processi meccanici responsabili dei fenomeni termodinamici; piuttosto aveva preso in considerazione sistemi meccanici semplici, con solo pochi gradi di libertà, per i quali fosse identificabile una funzione con le proprietà dell'entropia. è evidente, invece, che l'interesse di Boltzmann per questo approccio nasce dal suo obiettivo primario di trovare analogie meccaniche capaci di rendere chiara la relazione tra meccanica e termodinamica. In un articolo del 1885, über die Eigenschaften monozyklischer und anderer damit verwandter Systeme (Sulle proprietà dei sistemi monociclici e di altri a essi affini), egli introdusse e discusse, dandogli il nome di 'olodo', quello che in seguito sarebbe stato chiamato 'insieme canonico'. Tuttavia, mentre nella meccanica statistica l'insieme canonico serve a indagare sulle proprietà fisiche di sistemi del tutto generali in equilibrio termico a temperatura costante, il concetto introdotto da Boltzmann stabiliva semplicemente un'analogia meccanica, nel senso dei sistemi monociclici di Helmholtz. Questo esempio ci consente di chiarire un fatto generale: anche se la maggior parte degli elementi fondanti della meccanica statistica fu anticipata nel lavoro di Maxwell e di Boltzmann, tali elementi erano immersi in contesti concettuali diversi da quello della meccanica statistica moderna.

Oltre i gas

Un fattore essenziale della transizione verso la meccanica statistica moderna fu l'applicazione della teoria cinetica a sistemi diversi dai gas. Nel contesto ristretto dei gas la teoria cinetica serviva sostanzialmente a fornire un modello meccanico per la termodinamica e per i fenomeni di trasporto. Malgrado qualche successo sperimentale, essa conservò un carattere di precarietà, come appare evidente dai dibattiti in cui Boltzmann fu coinvolto. Tuttavia, verso la fine del secolo, la teoria cinetica fu applicata con successo a nuovi settori della fisica che riguardavano anche gli ioni e gli elettroni. Questo processo incoraggiò in modo naturale un rafforzamento e un ampliamento dei fondamenti di tale teoria.

Già nel 1857 Clausius aveva fornito una spiegazione qualitativa dei tre stati della materia e aveva tracciato schematicamente una rappresentazione cinetica dei passaggi di stato. La teoria del fisico olandese Johannes Diderik van der Waals (1837-1923) costituisce il primo tentativo coronato da successo di comprendere quantitativamente la transizione liquido-gas. La teoria cinetica di Clausius e di Maxwell era limitata ai gas ideali, per i quali la distanza media tra due molecole è molto più grande del loro diametro e le forze intermolecolari sono trascurabili tranne che durante le collisioni. Nel 1873, nello scritto Over die continuiteit van de gas- en vloeistoftoestand (Sulla continuità del gas e dello stato liquido), van der Waals lasciò cadere queste restrizioni con l'ambizione di creare una teoria cinetica dei liquidi. Il modello si basava su molecole sferiche, rigide ed elastiche, la cui attrazione reciproca diminuiva rapidamente all'aumentare della distanza, come ipotesi per spiegare lo stato liquido. In base al suo ragionamento, l'effetto di quest'ultima forza si limitava a un'attrazione delle molecole collocate sulla superficie del fluido verso l'interno. Da una parte, questa modificazione superficiale implica un fattore correttivo pari ad a/V² per la pressione P, che bilancia l'effetto dinamico degli urti sulla superficie stessa. Dall'altra, l'effetto dinamico si discosta dal valore ideale di Clausius (1/3)Nmu²/V, dato che la dimensione finita delle molecole altera il loro flusso vicino alla parete nella proporzione (V−B)/V, dove B è pari a quattro volte il volume totale delle sfere. Van der Waals usò con successo l'equazione di stato che derivava da queste assunzioni, (P+a/V²)(V−B)=RT, per una descrizione unitaria dello stato liquido e dello stato gassoso. Il suo modello, benché semplice e di scarso rigore, consente un'efficace rappresentazione delle proprietà più ovvie dei fluidi reali e sia Maxwell sia Boltzmann contribuirono a diffonderlo.

Un altro esempio, successivo, della generalizzazione dei metodi della teoria cinetica a sistemi diversi dai gas è costituito dalla teoria di Planck della radiazione termica, sviluppata tra il 1896 e il 1900. Di fatto Planck apparteneva alla schiera degli scettici riguardo alla teoria cinetica ed era inizialmente convinto che le proprietà termiche della radiazione potessero essere spiegate senza ricorrere ai metodi della fisica statistica. Il suo scetticismo nasceva dalla fede nella validità assoluta dei principî della termodinamica. Ai suoi occhi l'interpretazione boltzmanniana della legge dell'entropia non poteva essere vera, dato che essa assegnava a tale legge solo una validità statistica. Egli, invece, credeva che la diffusione delle onde elettromagnetiche da parte di risonatori elettrici fosse un processo intrinsecamente irreversibile dal quale poteva essere ricavato l'aumento di entropia. Tuttavia, in seguito alle pressanti critiche di Boltzmann, ben presto Planck dovette ammettere che occorreva introdurre l'ipotesi aggiuntiva della 'radiazione naturale', che costituiva l'esatta controparte di quella relativa al 'caos molecolare', anche senza accettare la concezione statistica di 'disordine' adottata da Boltzmann. Secondo Planck, la complessità dell'invisibile dinamica dei risonatori, o quella delle pareti del recipiente contenente il gas, garantiva un'evoluzione strettamente irreversibile del sistema, in piena armonia con la sua concezione assoluta della seconda legge della termodinamica. Il concetto di 'disordine elementare', che si riferiva genericamente sia alla radiazione naturale sia al caos molecolare, assumeva così un ruolo centrale nella trattazione in termini non statistici della relazione tra micromondo e macromondo.

La reinterpretazione dei metodi cinetici di Boltzmann fornita da Planck non si fermò qui. Nel 1900 lo sviluppo delle ricerche sulla radiazione termica lo portò a utilizzare la relazione di Boltzmann tra entropia S e probabilità W, anche se il carattere puramente formale della procedura gli impedì di intravedere le conseguenze rivoluzionarie del suo approccio. Egli giustificò la nuova formula per lo spettro di equilibrio della radiazione (la legge del corpo nero di Planck) basandosi sul conteggio boltzmanniano delle complessioni, ma reinterpretandolo come valutazione del disordine elementare che caratterizzava i risonatori della stessa frequenza ν. In questo procedimento si inserivano gli elementi finiti di energia hν, con h costante di Planck, ma senza entrare in contraddizione con la dinamica continua dei risonatori e con la natura continua della radiazione. In questo contesto Planck scrisse la formula che rappresentava l'interpretazione statistica dell'entropia e che ora appare sulla tomba di Boltzmann: S=klnW, con k costante di Boltzmann e W numero di microstati compatibile con un dato macrostato. Eppure egli continuò a non accettare la validità statistica della legge dell'entropia fino al 1914. I primi a trattare la radiazione del corpo nero come un sistema statistico furono Einstein ed Ehrenfest, arrivando così a dimostrare la sua incompatibilità con le leggi della fisica classica.

L'interesse per la teoria cinetica di Maxwell e di Boltzmann crebbe notevolmente verso la fine del secolo, con l'affermazione delle concezioni atomistiche e dei metodi statistici nella fisica dell'epoca. Gli esempi più eclatanti sono la teoria dell'elettrone di Hendrik Antoon Lorentz (1853-1928) ‒ una versione atomistica dell'elettromagnetismo maxwelliano ‒, la teoria elettronica dei metalli di Paul Drude (1863-1906), la teoria ionica della conduzione elettrolitica, la teoria cinetica delle soluzioni e l'uso di modelli atomici in chimica organica e inorganica. La ricerca sperimentale trovava occasioni inedite di sviluppo: si presentavano nuovi tipi di radiazione, sia di natura ondulatoria sia di natura corpuscolare; si manifestavano nuove forme di interazione tra radiazione e materia, come l'effetto Zeeman e l'effetto fotoelettrico, che confermavano la validità dei modelli atomistici della materia o ne suggerivano nuovi; le nuove ricerche sulle sospensioni colloidali sembravano rendere osservabili i moti molecolari, e via discorrendo. Nello stesso tempo si potevano ottenere stime del numero di Avogadro partendo da fonti diverse, come lo studio della capillarità, la teoria cinetica dei gas, gli esperimenti su film sottili e, sorprendentemente, anche dalla teoria della radiazione del corpo nero. La concordanza tra i valori ottenuti non solo fece crescere la fiducia nelle ipotesi atomistiche, ma rese anche più urgente l'elaborazione di teorie molecolari che collegassero tra loro i diversi settori della fisica.

Le formulazioni di Gibbs e di Einstein

All'inizio del XX sec. Gibbs ed Einstein proposero due versioni della meccanica statistica. Essi erano entrambi convinti che il loro lavoro non costituisse un contributo fondamentalmente originale, ma solo un cambiamento di prospettiva rispetto a quello che Maxwell, Boltzmann e altri avevano già ottenuto. I loro approcci, invece, spostavano l'enfasi della trattazione e introducevano un'organizzazione concettuale diversa rispetto agli approcci globali precedenti.

L'interesse di Gibbs era più matematico e più astratto rispetto a quello dei suoi predecessori. Essendo consapevole del moltiplicarsi delle teorie molecolari alla fine del XIX sec., egli diffidava delle ipotesi molecolari specifiche e quindi intendeva impostare la fisica statistica su basi il più possibile generali. La strategia di Gibbs era quella di sviluppare lo studio degli insiemi statistici (ensembles) di per sé e quindi di cercare le analogie tra le proprietà di tali insiemi e le leggi della termodinamica. La parte prevalente dei suoi Elementary principles of statistical mechanics del 1902 era dedicata alla descrizione puramente formale del sistema meccanico posto alla base della teoria; descrizione che era effettuata in termini di coordinate generalizzate regolate dalle equazioni di Hamilton, dal momento che egli concordava con Maxwell sul fatto che le violazioni dell'equipartizione dell'energia mettevano in dubbio i fondamenti della dinamica molecolare. Egli introdusse e analizzò sistematicamente i tre tipi fondamentali di insiemi della meccanica statistica: il microcanonico, il canonico e il grancanonico (nel quale poteva variare il numero delle molecole). Gibbs prese in esame le relazioni tra questi tre insiemi e le loro analogie con i sistemi termodinamici, comprese le formule per le fluttuazioni. Diversamente da Boltzmann, egli non cercò di fornire una giustificazione a priori del significato termodinamico dei suoi insiemi; il suo approccio era essenzialmente assiomatico.

Einstein, che non conosceva i Principles di Gibbs, affrontò la termodinamica statistica introducendo un punto di vista ancora diverso, con risultati parzialmente analoghi ma con scopi decisamente nuovi. Quando era studente egli era rimasto impressionato dallo sviluppo della fisica molecolare, nonostante lo scetticismo di molti fisici tedeschi. In particolare, lo colpì la teoria dei metalli di Drude del 1900, che combinava la teoria dell'elettrone di Lorentz con quella cinetica di Boltzmann. Sulla base dell'esperienza fatta sulle applicazioni dei metodi della teoria cinetica, ivi compreso il lavoro di Planck sulla radiazione termica, egli percepì l'approccio di Boltzmann come troppo centrato sulla fondazione meccanica della termodinamica e troppo poco orientato verso le recenti conferme sperimentali della concezione atomistica della materia e della radiazione. Dal suo punto di vista i metodi di Boltzmann erano lacunosi, anche perché egli li conosceva solo in maniera frammentaria attraverso la lettura delle Vorlesungen über Gastheorie. Gli articoli di Einstein, scritti tra il 1902 e il 1904, aspiravano quindi a dare nuovi fondamenti alla meccanica statistica.

Sfruttando i metodi che aveva appreso da Boltzmann, Einstein ricavò la seconda legge della termodinamica da un insieme canonico con forze esterne lentamente variabili, giustificando l'assunzione che tale insieme rappresentasse un sistema fisico a una data temperatura in base al fatto che esso poteva essere considerato un piccolo sottoinsieme dell'insieme microcanonico. Egli dava inoltre un'interpretazione fisica delle probabilità introdotte in quanto misure della frazione di tempo che il sistema trascorreva nelle varie configurazioni.

Ciò che distingueva Einstein dai suoi predecessori era una differenza di accento che si rivelò poi ricca di conseguenze. Boltzmann, per esempio, aveva mostrato la propria capacità di trovare le leggi macroscopiche della termodinamica e aveva minimizzato le divergenze da queste leggi che derivavano dalla struttura molecolare della materia. Einstein ebbe un atteggiamento opposto: egli desiderava usare la meccanica statistica per dimostrare la struttura molecolare della materia e per sondare la struttura non classica della radiazione. Per questa ragione concentrò la sua attenzione su quelle fluttuazioni rispetto allo stato di equilibrio che erano trascurabili per Boltzmann e inesistenti per Planck. La probabilità che compariva nella relazione di Boltzmann-Planck (S=klnW) era interpretata da Einstein in termini di frequenza temporale delle fluttuazioni di un sistema, la costante k come misura della 'stabilità termica'. Nel 1905, la sua analisi del moto browniano mostrò come le fluttuazioni potessero diventare osservabili in sistemi mesoscopici. Nello stesso tempo, attraverso una sorta di 'inversione' della relazione di Boltzmann, cercò di esplorare gli aspetti sconosciuti della dinamica dei microsistemi. Fu con questo procedimento che egli giunse a formulare l'ipotesi dei quanti di luce. Mentre Maxwell e Boltzmann intendevano stabilire i fondamenti meccanici della termodinamica, Einstein usò la meccanica statistica per mettere in discussione questi stessi fondamenti.

L'eredità di Boltzmann

Gibbs ed Einstein, nella loro formulazione sintetica della meccanica statistica, effettuarono una selezione e una reinterpretazione di alcuni aspetti del lavoro di Maxwell e di Boltzmann; ne trascurarono però altri che erano essenziali sia per Maxwell sia per Boltzmann, per esempio la discussione dei processi irreversibili e i fenomeni di trasporto. Più fedele a Boltzmann fu il suo allievo Ehrenfest, che tentò assieme alla moglie Tatiana di mettere in evidenza le connessioni tra i vari approcci di Boltzmann e di chiarire le ipotesi probabilistiche più rilevanti. Il loro lavoro enciclopedico del 1911 ‒ Begriffliche Grundlagen der statistischen Auffassung in der Mechanik (Fondamenti concettuali dell'interpretazione statistica in meccanica) ‒ resta una sintesi significativa delle idee di Boltzmann. Essi condividevano lo scetticismo di quest'ultimo verso l'ipotesi ergodica a un punto tale che Ehrenfest pensò che vi fosse una connessione tra le proprietà quantistiche e le violazioni dell'ergodicità. Essi si occuparono a lungo dei processi irreversibili, dell'equazione di Boltzmann e della curva H rimproverando, nello stesso tempo, Gibbs per aver trascurato questa parte dell'eredità di Boltzmann e aver a mala pena notato i contributi di Einstein.

La meccanica statistica è ora divenuta una parte essenziale della fisica. Tuttavia la diversità di approcci che ha caratterizzato la sua creazione è tuttora viva. Inoltre, la natura e la solidità dei suoi fondamenti restano questioni ancora da risolvere. I fisici e i matematici tuttora discutono sulla pertinenza dell'ipotesi ergodica e sulla distinzione tra processi reversibili e processi irreversibili. I filosofi continuano a riflettere sulle varie interpretazioni del concetto di probabilità e sulla freccia del tempo. Un secolo dopo la sua nascita, la meccanica statistica è ancora aperta e viva come Maxwell e Boltzmann volevano che fosse ogni teoria fisica.

Bibliografia

Brush 1965-72: Brush, Stephen G., Kinetic theory, New York, Pergamon, 1965-1972, 3 v.

‒ 1976: Brush, Stephen G., The kind of motion we call heat. A history of the kinetic theory of gases in the 19th century, Amsterdam, North Holland, 1976, 2 v.

‒ 1983: Brush, Stephen G., Statistical physics and the atomic theory of matter, from Boyle and Newton to Landau and Onsager, Princeton, Princeton University Press, 1983.

Darrigol 1988-91: Darrigol, Olivier, Statistics and combinatorics in early quantum theory, ‟Historical studies in the physical sciences", 19, 1988, pp. 17-80; 21, 1991, pp. 237-298.

Everitt 1975: Everitt, C.W. Francis, James Clerk Maxwell. Physicist and natural philosopher, Cambridge, Scribner's Sons, 1975 (rist. in: Maxwell, James Clerk, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner's Sons, 1970-1990, 18 v.; v. IX, 1981, pp. 198-230).

Fox 1971: Fox, Robert, The caloric theory of gases. From Lavoisier to Regnault, Oxford, Clarendon, 1971.

Gallavotti 1995: Gallavotti, Giovanni, Ergodicity, ensembles, irreversibility in Boltzmann's and beyond, "Journal of statistical physics", 78, 1995, pp. 1571-1589.

Garber 1986: Garber, Elizabeth - Brush, Stephen G. - Everitt, C.W. Francis, Introduction, in: Maxwell on molecules and gases, edited by Elizabeth Garber, Stephen G. Brush and C.W. Francis Everitt, Cambridge (Mass.), MIT Press, 1986.

Klein 1970a: Klein, Martin J., Paul Ehrenfest, Amsterdam, North Holland, 1970.

‒ 1970b: Klein, Martin J., Maxwell, his demon, and the second law of thermodynamics, "American scientist", 58, 1970, pp. 84-97.

‒ 1972a: Klein, Martin J., Mechanical explanation at the end of the nineteenth century, "Centaurus", 17, 1972, pp. 58-82.

‒ 1972b: Klein, Martin J., Gibbs, Josiah Willard, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner's Sons, 1970-1990, 18 v.; v. V, 1972, pp. 386-393.

‒ 1973: Klein, Martin J., The development of Boltzmann's statistical ideas, in: The Boltzmann equation. Theory and applications, edited by Ezechiel G.D. Cohen and Walter Thirring, Wien-New York, Springer, 1973, pp. 53-106.

Knott 1911: Knott, Cargill G., Life and scientific work of Peter Guthrie Tait, Cambridge, Cambridge University Press, 1911.

Plato 1991: Plato, Jan von, Boltzmann's ergodic hypothesis, "Archive for history of exact sciences", 42, 1991, pp. 71-89.

‒ 1994: Plato, Jan von, Creating modern probability. Its mathematics, physics, and philosophy in historical perspective, Cambridge, Cambridge University Press, 1994.

Porter 1986: Porter, Theodore M., The rise of statistical thinking, 1820-1900, Princeton, Princeton University Press, 1986.

Renn 1997: Renn, Jürgen, Einstein's controversy with Drude and the origin of statistical mechanics: a new glimpse from the 'love letters', "Archive for the history of exact sciences", 51, 1997, pp. 315-354.

Sklar 1993: Sklar, Lawrence, Physics and chance. Philosophical issues in the foundations of statistical mechanics, Cambridge, Cambridge University Press, 1993.