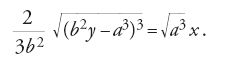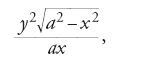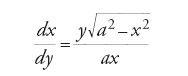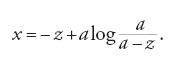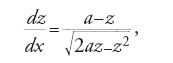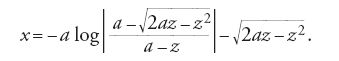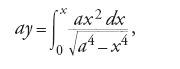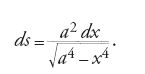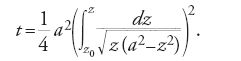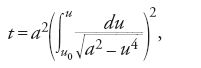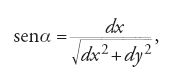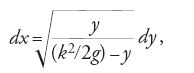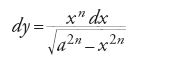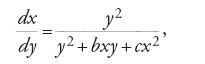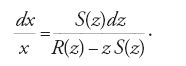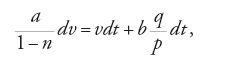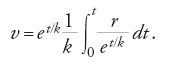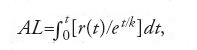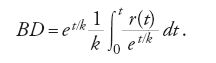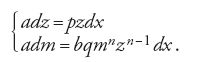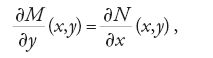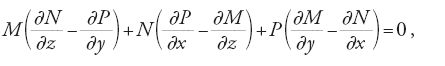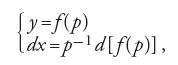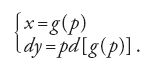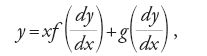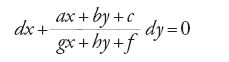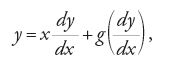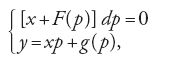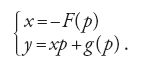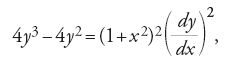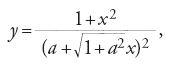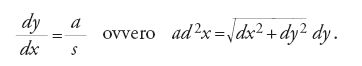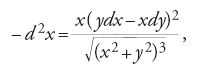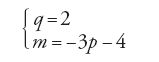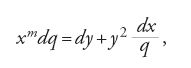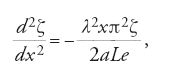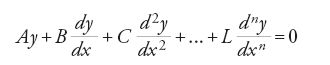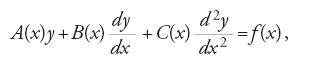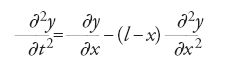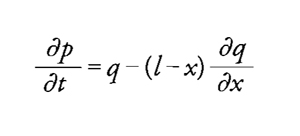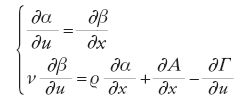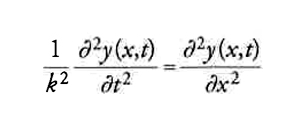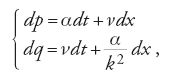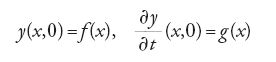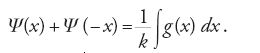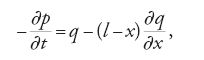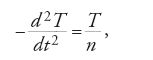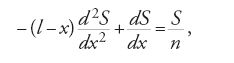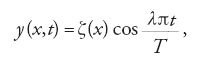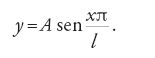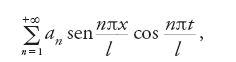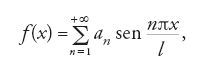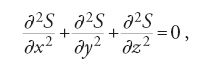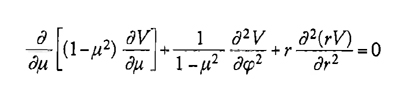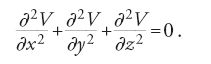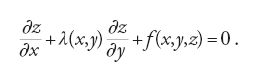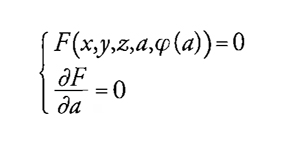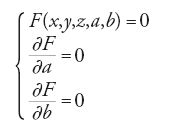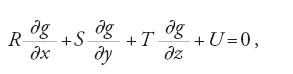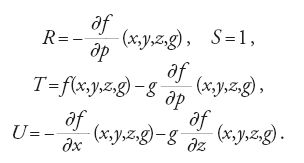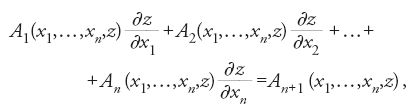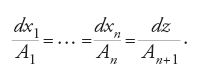L'Età dei Lumi: matematica. Le equazioni differenziali

L'Eta dei Lumi: matematica. Le equazioni differenziali

Le equazioni differenziali

E con la nascita del calcolo infinitesimale di Newton e di Leibniz, nella seconda metà del XVII sec., che compaiono i primi studi sulle equazioni differenziali. Essi hanno origine con il cosiddetto 'problema inverso delle tangenti', che consiste nel determinare la natura della curva che soddisfa una data relazione fra le coordinate e i loro elementi differenziali (o momenti delle flussioni): per esempio, una data proprietà sulla tangente o sulla normale, o sulla sottotangente. Dunque il problema inverso delle tangenti corrisponde a risolvere un'equazione differenziale del primo ordine. Il contesto iniziale è dunque geometrico, ma si estende in breve tempo ad altre branche della scienza, quali la meccanica, l'ottica, l'astronomia, l'idrodinamica e la iatromatematica. Fra i primi e più celebri problemi affrontati con successo tra l'ultimo decennio del XVII sec. e l'inizio del XVIII, ricordiamo, per esempio, quelli che portarono alla determinazione di curve trascendenti, come la catenaria, la trattrice, la brachistocrona, il discusso problema delle famiglie di traiettorie ortogonali e gli studi sul moto di un corpo soggetto a un campo di forze centrali nel vuoto o in un mezzo resistente. Da una congerie di esempi specifici di questo tipo si passa a individuare, già negli anni Novanta del Seicento, metodi adatti a risolvere particolari classi di equazioni differenziali: sostituzioni e separazione delle variabili condussero alla soluzione delle equazioni omogenee, delle equazioni lineari del primo ordine e delle equazioni di Bernoulli. Inoltre, nel volgere di pochi anni a cavallo dei due secoli, si assiste a un graduale trapasso da ricerche ancora segnate da una forte impronta geometrica a studi di carattere puramente analitico.

Gli approcci degli esponenti delle due scuole, newtoniana e leibniziana, alla soluzione delle equazioni differenziali presentano fin dall'inizio elementi di diversità, che permangono nel corso del Settecento. Gli Inglesi privilegiano l'uso delle serie come strumento fondamentale nel calcolo integrale e Newton fornisce una soluzione generale del problema dell'integrazione delle equazioni differenziali in termini di serie di potenze. I leibniziani preferiscono invece ricercare soluzioni in termini finiti, vale a dire soluzioni in cui le funzioni incognite sono espresse tramite un numero finito di operazioni algebriche tra funzioni elementari. Quando ciò non è possibile essi ricorrono, inoltre, alla cosiddetta 'integrazione per quadrature', in cui le funzioni incognite sono espresse anche mediante un numero finito di integrali indefiniti.

Tra la fine del Seicento e la prima metà del Settecento, tutti i matematici più autorevoli si applicano per risolvere le equazioni differenziali che si presentavano sempre più numerose nello studio di problemi geometrici o fisico-matematici. Dalle loro ricerche scaturisce un caleidoscopio di idee e di metodi che porta, nella seconda metà del XVIII sec., alla costituzione di una teoria autonoma. Alla fine del secolo la trattazione sistematica delle equazioni differenziali ordinarie si può considerare definita, almeno per ciò che concerne i metodi elementari di risoluzione (separazione delle variabili, sostituzioni, fattori integranti), l'individuazione della soluzione generale per alcune classi di equazioni (equazioni lineari, di Bernoulli, di d'Alembert, di Clairaut) e i concetti basilari (soluzione generale, particolare, singolare).Per i risultati fondamentali, quali il teorema di esistenza e unicità locale delle soluzioni per il problema con condizioni iniziali, si devono attendere le lezioni tenute da Augustin-Louis Cauchy all'École Polytechnique nel 1823-1824, mentre per lo studio della dipendenza dai dati occorre giungere alla fine del XIX secolo.

Per quanto riguarda le equazioni alle derivate parziali, i matematici del Settecento non hanno ancora gli strumenti tecnici per trattarle, eccetto per alcuni casi particolari che provengono spesso da problemi di meccanica o di fisica. Il caso più celebre, che coinvolge tutti gli studiosi più eminenti e dà l'avvio ad accesi dibattiti nella seconda metà del Settecento, riguarda l'equazione della corda vibrante e questo è anche l'unico caso esaminato in modo approfondito e generale. A cavallo tra la fine del XVIII e l'inizio del XIX sec., si ottengono risultati importanti per la teoria delle equazioni alle derivate parziali del primo ordine. Tuttavia si devono attendere gli anni Venti del XIX sec. per avere, con Cauchy, una rappresentazione generale della soluzione di un'equazione alle derivate parziali lineare a coefficienti costanti, con assegnate condizioni iniziali, e gli anni Quaranta per il primo teorema di esistenza e unicità locale delle soluzioni analitiche di un sistema di equazioni analitiche, lineari rispetto alle derivate parziali delle funzioni incognite e con condizioni iniziali analitiche, ancora una volta dovuto a Cauchy.

Ci proponiamo ora di ripercorrere, in ordine cronologico, quelle che, a nostro avviso, sono le tappe più significative della storia delle equazioni differenziali ordinarie e alle derivate parziali.

Il problema inverso delle tangenti e le equazioni differenziali ordinarie del primo ordine

La prima soluzione edita di un'equazione differenziale riguarda il celebre problema, proposto da Florimond de Beaune (1601-1652) a Descartes, di determinare la curva di sottotangente costante, che equivale a risolvere l'equazione differenziale y(dx/dy)=c. Tale soluzione compare nel 1684 in appendice alla prima esposizione del calcolo differenziale di Leibniz ed è ottenuta osservando che, fissato il differenziale dell'ascissa dx=b costante, infinitesimo, alla successione delle ascisse in progressione aritmetica corrisponde una successione di ordinate in progressione geometrica, per cui la curva soluzione è una "logaritmica", corrispondente al grafico di una funzione esponenziale.

A partire dal 1690, sugli "Acta Eruditorum", Leibniz e i fratelli Jakob I (1654-1705) e Johann I (1667-1748) Bernoulli pubblicano una messe incredibile di soluzioni di problemi difficili e di grande attualità, risolti con eleganza e scioltezza, nei quali le equazioni differenziali giocano un ruolo di primo piano. A proposito di questi risultati, l'insigne matematico Christiaan Huygens (1629-1695), che aveva assistito alla nascita del calcolo differenziale, scriverà a Leibniz nel maggio del 1694: "Vi siete riservato dei veri colpi da maestro, Signore, […]. Potreste stendere un eccellente trattato sugli usi diversi di questo calcolo, e io vi esorto a questo compito come a un'opera di grande bellezza e utilità, che deve venire da voi piuttosto che da qualsiasi altro" (Leibniz, Mathematische Schriften, I, pp. 174-175).

Tra le prime questioni affrontate, emerge il problema proposto da Leibniz ai cartesiani sulle "Nouvelles de la République des Lettres" del settembre del 1687, che si inseriva nell'acceso dibattito sulla misura delle forze vive. Esso consiste nel determinare la natura della curva isocrona, cioè della curva lungo la quale un corpo soggetto al suo peso discende uniformemente e si avvicina ugualmente all'orizzonte in tempi uguali (velocità costante −b nella direzione verticale). Nell'ottobre del 1687, sulla stessa rivista, Huygens presenta la soluzione senza la relativa dimostrazione e nel 1689 Leibniz, ritornando sulla questione negli "Acta Eruditorum", verifica che la curva "parabolica quadrato-cubica" soddisfa il problema. Si deve però a Jakob I Bernoulli la pubblicazione, nell'articolo Analysis problematis del 1690, della formulazione e trattazione analitica dello stesso problema, con l'uso del calcolo leibniziano. Giunto all'equazione differenziale a variabili separate

Bernoulli determina analiticamente la curva isocrona soluzione integrando: "Ergo et horum integralia aequantur" (p. 218),

Quando l'equazione differenziale non si presenta a variabili separate, il procedimento utilizzato per costruire le soluzioni tramite le quadrature è la separazione delle variabili, cui si perveniva, se necessario, con opportune sostituzioni. Per esempio, Leibniz nel 1691, nel suo carteggio con Huygens, risolve il problema di determinare le curve di sottotangente uguale a

che si riconduce all'equazione differenziale a variabili separabili

e trova tre soluzioni. Negli "Acta Eruditorum" del 1694, sia Jakob I Bernoulli sia suo fratello Johann I, dopo aver ricordato le innumerevoli regole particolari da loro ideate per separare le variabili nelle equazioni differenziali del primo ordine, osservano acutamente che non si può sperare di determinare una regola generale che fornisca la separazione delle variabili in un'equazione qualunque.

fig. 2

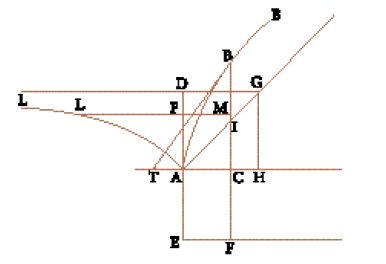
Un caso in cui la separazione delle variabili si ottiene facilmente tramite un'opportuna sostituzione è il problema di de Beaune (fig. 2), presentato da Johann I Bernoulli e Guillaume-François-Antoine de L'Hôpital (1661-1704) sul "Journal des Sçavants" nel 1692 e sugli "Acta Eruditorum" nel 1693. Date le rette AC e AI che formano l'angolo CAI di 45°, trovare la curva ABB riferita all'asse AC, tale che, condotte da un suo punto qualunque B l'ordinata BC, la tangente BT e la sottotangente CT, si abbia BC/CT=a/BI, con a costante assegnata. La costruzione geometrica della soluzione è data da Bernoulli senza la relativa trattazione analitica. Essa dipende dalla quadratura dell'iperbole, dal momento che il problema proposto corrisponde a risolvere l'equazione differenziale dy/dx=a/(y−x) che, con la sostituzione z=y−x, diventa zdz/(a−z)=dx. Integrando e imponendo la condizione z(0)=0 si ottiene infatti

Un altro risultato interessante è la soluzione, pubblicata da Leibniz nel settembre del 1693, del problema della trattrice, che Claude Perrault (1613-1688) gli aveva posto all'epoca del suo soggiorno a Parigi (1672-1676), problema consistente nella determinazione della curva descritta su un piano orizzontale da un corpo pesante legato a un estremo di una corda il cui altro estremo si muove lungo una retta fissa situata in quel piano. La proprietà geometrica caratteristica della curva è dunque che in ogni suo punto il segmento di tangente compreso tra il punto stesso e la retta fissa ha lunghezza costante a uguale alla lunghezza della corda. Da tale proprietà si deduce l'equazione differenziale

di cui Leibniz fornisce la costruzione geometrica, legata alla quadratura dell'iperbole. Integrando la [6] e imponendo la condizione z(0)=0, troviamo infatti che la trattrice è la curva trascendente di equazione

Anche gli studi sull'elasticità danno luogo ad altri notevoli contributi nell'ambito delle equazioni differenziali. Nel 1691 Jakob I Bernoulli pone il problema di determinare la forma di una trave uniforme ed elastica sotto tensione, supponendo che essa sia fissata verticalmente a un estremo e che un peso sia attaccato all'altro estremo in modo da mantenerlo orizzontale. Nel giugno del 1694 egli stesso pubblica la soluzione del problema, che, nel caso in cui, secondo la legge di Hooke, le estensioni siano proporzionali alle forze applicate in ciascun punto, conduce all'equazione differenziale dell'elastica

ove a è la distanza orizzontale fra i due estremi della trave. Bernoulli fornisce la costruzione geometrica per quadrature della soluzione, che corrisponde alla formula analitica

e inoltre calcola il differenziale dell'arco di lunghezza s, precisamente

Quest'ultimo risultato è da lui collegato immediatamente a un altro celebre problema di grande attualità, quello dell'isocrona paracentrica, proposto da Leibniz ai cartesiani nel 1689: stabilire la natura della curva lungo la quale la caduta di un corpo, soggetto al suo peso, è tale che esso si allontana o si avvicina uniformemente da un punto assegnato, ossia determinare il luogo dei punti per i quali la distanza dal punto fisso, al tempo t, è proporzionale a t. Nello stesso mese del 1694 Jakob I Bernoulli pubblica, infatti, un secondo articolo nel quale considera l'equazione differenziale dell'isocrona paracentrica, che era già stata ricavata da suo fratello Johann all'epoca del soggiorno parigino (1691-1692):

Dopo aver rilevato che di quest'equazione non erano state date né la soluzione analitica né la costruzione geometrica, a causa delle difficoltà nella separazione delle variabili, Bernoulli mostra come questa sia possibile quando si operino le sostituzioni ay=tz e ax=t(a2−z2)1/2 e fornisce la costruzione geometrica della curva soluzione, la cui espressione analitica dipende da un integrale ellittico:

Ponendo z=u2 si ottiene

in cui l'integrale a secondo membro rappresenta la lunghezza di un arco dell'elastica; pertanto Bernoulli costruisce l'isocrona paracentrica tramite una rettificazione. In un successivo articolo, pubblicato nel settembre dello stesso anno sugli "Acta Eruditorum", egli riconduce la costruzione della stessa curva alla rettificazione della lemniscata.

Un altro famoso problema su cui si cimentano i pionieri del nuovo calcolo è quello della brachistocrona, proposto pubblicamente nel 1696 da Johann I Bernoulli: dati due punti A e B in un piano verticale, determinare la curva descritta da un corpo soggetto al suo peso che partendo da A raggiunga B nel minor tempo possibile. Già Galilei nei Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla mecanica et i movimenti locali (1638) aveva mostrato che il cammino più veloce percorso da un corpo pesante fra due punti assegnati non coincide con quello più breve, cioè con il segmento congiungente i due punti; egli tuttavia aveva erroneamente dedotto che il cammino più veloce avviene lungo un arco di cerchio. Sul numero di maggio degli "Acta Eruditorum" del 1697 compaiono ben sei soluzioni corrette del problema, da parte di Leibniz, Johann I Bernoulli, Jakob I Bernoulli, L'Hôpital ed Ehrenfried Walther von Tschirnhaus (1651-1708); lsoluzione è anonima e fu concordemente attribuita a Newton, su suggerimento di Johann I Bernoulli che aveva riconosciuto ex ungue leonem. Bernoulli riconduce il problema in modo elegante a un'equazione differenziale, sulla base di un'analogia con un problema di ottica, fondata sul principio di Fermat, secondo cui la Natura si serve sempre dei mezzi e delle vie più facili e più veloci. Precisamente, egli individua la brachistocrona come la curva descritta da un raggio di luce che si propaghi in un mezzo la cui densità è inversamente proporzionale alla velocità che un grave acquisterebbe cadendo. In ogni punto è perciò v=(2gy)1/2 e per la legge di rifrazione risulta v/senα=k, ove α è l'angolo formato fra la tangente e la verticale in quel punto. Poiché

Bernoulli ottiene

da cui conclude che la curva è una cicloide.

Alla fine di questo articolo, Bernoulli propone pubblicamente il problema di determinare le traiettorie ortogonali a una famiglia di curve logaritmiche. Tali questioni, legate al problema più generale di trovare la famiglia di curve che taglino secondo un angolo dato un'altra famiglia di curve assegnata, erano già apparse nella corrispondenza fra Leibniz e i Bernoulli fin dal 1694; ma ètra la fine del Seicento e gli inizi del Settecento che riceve grande attenzione da parte dei matematici, sia del Continente sia inglesi, i quali concentrano sforzi ed energie alla ricerca di un metodo generale di soluzione. È infatti in occasione della disputa sulla priorità dell'invenzione del calcolo che Leibniz e Johann I Bernoulli, fra il 1715 e il 1716, ripropongono come sfida ai newtoniani problemi di traiettorie ortogonali, che ritengono atti a dimostrare quanto profonda sia la loro abilità nel risolvere le equazioni differenziali. In particolare, soluzioni del difficile problema di determinare la famiglia delle traiettorie ortogonali alle curve soluzione dell'equazione differenziale

sono state pubblicate da Jacob Hermann e Brook Taylor nel 1717, da Johann I Bernoulli e suo figlio Nikolaus II nel 1718 e da Nikolaus I Bernoulli nel 1719.

Fin dai primi studi sulle equazioni differenziali i leibniziani s'interrogano sulla possibilità di determinare procedimenti atti a risolvere specifiche classi di equazioni. Le equazioni differenziali omogenee sono le prime a presentarsi alla loro attenzione ed essi individuano facilmente la sostituzione generale che consente la separazione delle variabili. Già in una lettera destinata a L'Hôpital del 1692-1693, Leibniz afferma di saper ridurre alle quadrature le equazioni differenziali omogenee, quale per esempio

e anche Johann I Bernoulli conosce la sostituzione che separa le variabili, come risulta sia dalle Lectiones che diede a L'Hôpital nel 1691-1692, sia dalla lettera a Leibniz del maggio del 1694. La pubblicazione della regola generale per le equazioni omogenee risale però al 1714 con l'articolo di Gabriele Manfredi edito sul "Giornale de' Letterati d'Italia". Egli considera l'equazione T(x,y)dx=U(x,y)dy, dove T e U sono funzioni omogenee dello stesso grado, e con la sostituzione y=zx ottiene l'equazione a variabili separate

Altre importanti classi di equazioni ordinarie, la cui soluzione è determinata sugli "Acta Eruditorum" alla fine del XVII sec., sono le equazioni lineari del primo ordine e le cosiddette 'equazioni di Bernoulli'.

Nel 1695, al termine di un lungo articolo interamente dedicato alle equazioni differenziali, Jakob I Bernoulli propone il problema di separare le variabili, ossia di costruire per quadrature l'equazione differenziale che per questo da lui prende il nome

[19] ady=pydx+bqyⁿdx,

dove p e q dipendono soltanto da x.

Nella Notatiuncula del 1696 Leibniz afferma semplicemente di aver ricondotto tale equazione a un'equazione differenziale lineare, di cui ha già comunicato agli amici il metodo generale di risoluzione, e pertanto non giudica necessario fornire ulteriori spiegazioni. Egli infatti aveva trasmesso per lettera a L'Hôpital, nel novembre del 1694, una soluzione della generica equazione lineare non omogenea del primo ordine, mostrando che essa soddisfa l'equazione data. Precisamente, per l'equazione

[20] mdx+nydx+dy=0,

ove m e n dipendono solo da x, indicata con p la funzione tale che ∫(1/p)dp=∫ndx, aveva verificato che la funzione y, definita ponendo py+∫mpdx=0, è una soluzione dell'equazione di partenza.

Jakob I Bernoulli ritorna sulla sua equazione nel luglio del 1696 e negli Addenda del settembre 1697, che seguono cronologicamente la soluzione analitica della stessa equazione pubblicata da suo fratello Johann nel marzo 1697. Nel primo articolo Jakob, riprendendo le considerazioni di Leibniz, dapprima osserva che l'equazione da studiare è riconducibile a un'equazione lineare e poi mostra come si costruisce quest'ultima. Infatti l'equazione ady=pydx+bqyⁿdx, con le sostituzioni pdx=dt e y=v1/(1−ⁿ), diviene

che rappresenta un'equazione lineare non omogenea nell'incognita v=v(t), ove t=∫p(x)dx. Egli pertanto considera l'equazione differenziale lineare

[22] kdv=vdt+rdt,

ove k è costante e r dipende da t, e fornisce la costruzione geometrica di una soluzione. Tale costruzione equivale al seguente ragionamento analitico: posto v=mn, e sostituendo nell'equazione [22], risulta kmdn+kndm=mndt+rdt, che può essere soddisfatta semplicemente imponendo che sia

Osserviamo che la prima di queste due equazioni fornisce la soluzione n dell'equazione omogenea, mentre la seconda impone che mn sia una soluzione dell'equazione non omogenea; il metodo di risoluzione adottato, dunque, è quello che sarà poi denominato 'metodo della variazione delle costanti arbitrarie'. Dalla prima equazione segue che n=e^t/^k e quindi, sostituendo nella seconda, si ha kdm=(r/e^t/^k)dt, per cui in conclusione si ottiene

Per costruire geometricamente la funzione incognita v=v(t) Bernoulli considera allora la logaritmica FG di coordinate AB=t e BG=e^t/^k e, preso BC=r(t) e Af=k, costruisce BH come quarto proporzionale fra BG, BC e Af, per cui BH=kr/e^t/^k. Se l'area del rettangolo Af×AL uguaglia l'area della regione

per cui

l'ordinata v=v(t) da determinare non è altro che il segmento BD, quarto proporzionale fra Af, BG e AL, cioè

Johann I Bernoulli, per risolvere l'equazione proposta dal fratello, pone invece direttamente y=mz e ottiene l'equazione

[26] azdm+amdz=pmzdx+bqmⁿzⁿdx,

che può essere soddisfatta semplicemente imponendo

In questo modo la separazione delle variabili risulta effettuata ed è possibile determinare in modo algebrico oppure per quadrature sia z sia m e, di conseguenza, anche la funzione incognita y.

Tra gli artifici ideati dai primi studiosi delle equazioni differenziali e contenuti nelle lezioni date ai loro allievi, vogliamo ricordare quello che, successivamente elaborato e sviluppato, è diventato l'attuale metodo del fattore integrante. In certi casi particolari sia Johann I Bernoulli nelle Lectiones per L'Hôpital, sia Jacopo Riccati (1676-1754) nel trattato Della separazione delle indeterminate, composto nel 1722-1723 per gli allievi Lodovico da Riva (1698-1746) e Giuseppe Suzzi (1701-1764), consigliano di moltiplicare o dividere tutti i termini dell'equazione differenziale per un'opportuna potenza di x o di y, in modo da individuare immediatamente dei differenziali esatti.

Negli anni 1734-1735 la condizione per l'esattezza di una forma differenziale è osservata in maniera esplicita da Leonhard Euler (1707-1783), che in questa occasione utilizza anche fattori integranti. È negli articoli di Alexis-Claude Clairaut (1713-1765) editi sui "Mémoires de l'Académie Royale des Sciences" di Parigi del 1739 e del 1740 che troviamo la sistemazione teorica delle equazioni differenziali esatte. Qui egli dimostra che se l'equazione differenziale

[28] M(x,y)dx+N(x,y)dy=0

verifica la condizione

essa è integrabile e i suoi integrali sono dati nella forma implicita F(x,y)=c, ove la funzione F è tale che ∂F/∂x=M e ∂F/∂y=N. Inoltre, egli mostra come la primitiva F può essere ottenuta dalle funzioni M e N integrando opportunamente la prima rispetto a x e la seconda rispetto a y. Clairaut estende il risultato a funzioni di più variabili e determina opportuni fattori integranti; nel caso delle equazioni in tre variabili

[30] M(x,y,z)dx +N(x,y,z)dy +P(x,y,z)dz = 0

stabilisce la condizione di integrabilità

che garantisce l'esistenza di un fattore integrante.

Negli anni successivi Euler sviluppa notevolmente il metodo del fattore integrante tramite il quale ottiene integrali per quadrature e in un lungo studio del 1760-1761 pubblicato sui "Novi Commentarii", editi a Pietroburgo dall'Academia Scientiarum Imperialis Petropolitana, esamina le condizioni che debbono essere soddisfatte per l'esistenza di fattori integranti e individua numerose classi di equazioni per le quali è possibile determinare un fattore integrante.

Le equazioni ordinarie del primo ordine non esplicitabili rispetto a y′ e le soluzioni singolari

Le equazioni del primo ordine non esplicitabili rispetto al quoziente dy/dx, che si incontrano numerose nei problemi geometrici e nelle applicazioni, ricevono particolare attenzione da parte di vari studiosi. Nel caso di equazioni differenziali riconducibili alla forma y=f(dy/dx) oppure a x=g(dy/dx), essi individuano l'utilità della sostituzione dy=pdx per avere la soluzione in forma parametrica. Operata tale sostituzione si ottiene, infatti, nel primo caso

e nel secondo

Da questi sistemi si può trarre la soluzione in funzione del parametro p.

Jean-Baptiste Le Rond d'Alembert, in un articolo edito nel 1748 sull'"Histoire de l'Académie des Sciences" di Berlino, mostra che la sostituzione dy=pdx, utile nelle equazioni del primo ordine mancanti della x o della y, può applicarsi più in generale a equazioni del tipo

attualmente note in letteratura come equazioni di d'Alembert-Lagrange. Differenziando l'equazione si ha infatti

[35] [p-f (p)]dx=xd[f (p)]+d[g (p)]

con dy=pdx, da cui si ottiene la soluzione in funzione del parametro p, dal momento che la [35] è un'equazione lineare se p−f(p)≠0. Inoltre, d'Alembert osserva che casi particolari dell'equazione considerata sono, oltre alle equazioni omogenee, quelle del tipo

e quelle del tipo

oggi denominate 'equazioni di Clairaut'. Nel caso di queste ultime, differenziando ricava

e pertanto le soluzioni sono date dal fascio di rette di equazione y=cx+g(c) e dalla curva di equazioni parametriche

Poiché tale curva non può essere ottenuta dalla soluzione generale per alcun valore della costante arbitraria, siamo in presenza di una soluzione singolare.

I concetti di soluzione o integrale generale (o completo), di soluzione particolare e di soluzione singolare diventano gradualmente più chiari nel corso del XVIII sec., e la relativa terminologia non è univoca, ma varia da studioso a studioso.Per esempio, Joseph-Louis Lagrange (1736-1813) nel 1774 chiama integrali particolari le soluzioni singolari.

Già nel 1694, nel Modus generalis construendi omnes aequationes differentiales primi gradus, Johann I Bernoulli aveva mostrato che un'equazione differenziale del primo ordine ammette infinite soluzioni e Gabriele Manfredi, nel De constructione aequationum differentialium primi gradus (1707), aveva osservato che le soluzioni di un'equazione del primo ordine dipendono da una costante arbitraria, rilevando che in alcuni casi le curve così ottenute differiscono per una traslazione, mentre in altri casi cambia la natura della curva. I concetti di integrale generale e di integrale particolare sono stabiliti in modo esplicito da Euler in una memoria del 1743 in cui egli afferma che l'integrale completo di un'equazione ordinaria di ordine n dipende da n costanti arbitrarie e che gli integrali particolari si ottengono da quello completo assegnando alle costanti un valore fissato.

Si deve invece a Taylor la denominazione "soluzione singolare", introdotta nella Methodus incrementorum directa et inversa (1715) a proposito di una soluzione che non si può ottenere dall'integrale generale particolarizzando la costante arbitraria. Risolvendo l'equazione differenziale

egli determina, oltre alla soluzione generale

l'integrale y=1, "quae est singularis quaedam solutio problematis" (p.27). Clairaut, nei "Mémoires de l'Académie des Sciences" di Parigi del 1734, partendo da un problema geometrico, trova esempi di equazioni differenziali che ammettono soluzioni non comprese nell'integrale generale e queste ultime risolvono sia l'equazione differenziale sia il problema geometrico iniziale. Euler successivamente osserva che tali soluzioni singolari si ottengono differenziando, e non integrando, l'equazione da risolvere e mostra che la loro equazione cartesiana si ricava eliminando la p=dy/dx fra l'equazione data e la sua derivata rispetto a p. A lui si deve inoltre un criterio, che fu poi approfondito da Pierre-Simon de Laplace (1749-1827), per distinguere le soluzioni singolari dalle soluzioni particolari, senza conoscere la soluzione generale. Il contributo di Laplace, edito in una memoria del 1772, si applica anche alle equazioni differenziali in tre variabili e a quelle di ordine superiore.

L'interpretazione geometrica dell'integrale singolare, come inviluppo della famiglia di curve individuata dall'integrale generale, risale invece a Lagrange, che la ottiene come conseguenza di un metodo, da lui presentato nel 1774, per determinare gli integrali singolari a partire dall'integrale generale. Precisamente, il metodo consiste nel calcolare ∂y/∂c a partire dall'espressione dell'integrale generale V(x,y,c)=0 e nel ricercare le soluzioni singolari fra le soluzioni dell'equazione che si deduce eliminando la costante c fra le equazioni V=0 e ∂y/∂c=0. Lo stesso può farsi a partire da ∂x/∂c. Anche Leibniz aveva avuto un'intuizione di questo tipo, come risulta nel Nova calculi differentialis applicatio et usus, uno studio condotto nel 1694 sugli inviluppi di una famiglia di curve.

Le equazioni ordinarie di ordine superiore al primo e l'equazione di Riccati

Le equazioni differenziali di ordine superiore al primo s'incontrano fin dalle prime applicazioni del calcolo a problemi di geometria o di fisica matematica. Tra i primi esempi che conducono a equazioni di questo tipo troviamo il celebre problema della catenaria (già affrontato, ma non risolto, da Galilei nel 1638 e riproposto all'attenzione dei matematici da Jakob I Bernoulli nel 1690), ovvero il problema relativo alla determinazione della curva lungo la quale si dispone una fune flessibile, soggetta al suo peso, liberamente sospesa tra due punti fissi. Sugli "Acta Eruditorum" del 1691 appaiono le soluzioni di Leibniz, di Jakob I e Johann I Bernoulli, e di Huygens che, pur contenendo interessanti proprietà sulla curva, non indicano però il procedimento analitico di risoluzione. È nelle Lectiones mathematicae de methodo integralium (1691-1692) di Johann I Bernoulli che vediamo in quale modo i leibniziani possono aver dedotto la soluzione di questo problema, che si traduce nell'equazione differenziale del secondo ordine in cui manca la variabile indipendente y

In questo periodo molti matematici, fra cui Leibniz, i Bernoulli e Riccati, si dedicano alla ricerca di artifici atti ad abbassare l'ordine delle equazioni differenziali e su questo tema, all'inizio del XVIII sec., sorgono anche accesi dibattiti. Alludiamo, per esempio, alla polemica che fra il 1710 e il 1716 coinvolge Johann I e Nikolaus I Bernoulli, Hermann, Riccati e Giuseppe Verzaglia (1669-1730) sul problema inverso delle forze centrali, consistente nel determinare l'orbita descritta da un punto materiale soggetto a un campo di forze centrali con centro in un punto assegnato. Anche in questo caso uno dei molti temi oggetto di discussione riguarda il modo con cui Hermann, partendo dall'equazione del secondo ordine

è riuscito a ricondursi a una equazione del primo ordine.

Nel 1712 Riccati, esaminando il problema inverso dei raggi osculatori, ossia il problema di determinare la curva avente raggio di curvatura assegnato, mostra che un'equazione del secondo ordine in cui non compare esplicitamente la variabile indipendente è riducibile, con un'opportuna sostituzione, a un'equazione del primo ordine. Studi ulteriori negli anni Venti lo portano a generalizzare questo risultato e a concludere che ogni equazione del secondo ordine, in cui non compare esplicitamente una delle variabili, è riducibile al primo.In tal caso, infatti basta "prendere la prima differenza che fluisce, e porla uguale a una nuova incognita moltiplicata nella costante assunta, o che si assume ad arbitrio, in caso non fosse stata fissata costante" (Della separazione delle indeterminate nelle equazioni differenziali del primo grado, in Opere, I, p. 573). Riccati applica poi analoghe considerazioni a equazioni di ordine superiore al secondo. In questi stessi anni Euler inizia uno studio sistematico sulle equazioni differenziali di ordine superiore, ricercando metodi per abbassarne l'ordine. Lguida che egli segue si basa sull'osservazione che nella funzione esponenziale e nei suoi differenziali successivi la variabile indipendente si trova sempre soltanto all'esponente; quindi, se in un'equazione di ordine superiore si sostituisce un esponenziale a una variabile, quella variabile si troverà sempre solamente all'esponente e dunque, se è possibile semplificare l'esponenziale introdotto, si potrà eliminare dall'equazione una delle variabili, rientrando così nel caso considerato da Riccati. Euler individua poi tre classi di equazioni alle quali è sempre possibile applicare questo artificio. Approfondimenti successivi di questo tema s'incontrano nella memoria, pubblicata sui "Novi Commentarii" di Pietroburgo del 1758-1759, in cui Euler studia il problema di determinare fattori integranti finiti o differenziali per equazioni del secondo ordine e di ordine superiore. In particolare, egli dimostra che la conoscenza di un fattore integrante permette di abbassare di un'unità l'ordine dell'equazione e osserva che la conoscenza di due fattori integranti riduce alle quadrature il problema dell'integrazione di un'equazione del secondo ordine.

L'equazione non lineare del primo ordine, nota come 'equazione di Riccati',

[44] dy=ax^mdx+by²dx,

è strettamente connessa alle equazioni del secondo ordine e su di essa, nella prima metà del Settecento, si concentrano gli studi di numerosi matematici.

Già nel 1694 Johann I Bernoulli considera un caso particolare di quest'equazione, precisamente (x2+y2)dx=a2dy, allo scopo d'illustrare un suo metodo generale per costruire le equazioni del primo ordine, senza procedere alla separazione delle variabili. Suo fratello Jakob dà invece l'avvio, fra il 1694 e il 1696, ai primi studi sull'integrazione per serie dell'equazione di Riccati e in una lettera a Leibniz del 1702 comunica di essere riuscito a separare le variabili, nel caso particolare studiato da Johann, riconducendosi a un'equazione del secondo ordine.

Nuova attenzione è rivolta a questo argomento a partire dal 1718, allorché Riccati propone per lettera a Nikolaus I Bernoulli, tramite Giovanni Poleni (1683-1761), il problema di determinare i valori degli esponenti m, p e q per i quali è possibile ottenere la separazione delle variabili nell'equazione

[45] dy=ax^mdx+bx^py^qdx.

In questa stessa lettera Riccati afferma anche di aver ottenuto la separazione in quattro casi; fra questi è compreso quello relativo alle condizioni

che conduce all'equazione che porta il suo nome. In questi anni assistiamo a vivaci dibattiti e scambi di risultati in proposito fra i Bernoulli (Johann I, Nikolaus I, Nikolaus II e Daniel), i loro corrispondenti Christian Goldbach (1690-1764) e Pierre Rémond de Montmort (1678-1719) e gli italiani Riccati, Manfredi, Poleni, Giovanni Rizzetti (1675-1751) e Suzzi. Riccati, inoltre, è sollecitato dai Bernoulli a proporre pubblicamente nel 1722, sugli "Acta Eruditorum", il problema di determinare per quali valori di m l'equazione

dove q=xⁿ, è integrabile per quadrature. In seguito a tale proposta pubblica vengono editi molti dei risultati comunicati per lettera fra il 1721 e il 1722. Di particolare importanza sono quelli ottenuti da Daniel Bernoulli, il quale nel 1722, in una lettera a suo fratello Nikolaus II, dimostra che è possibile separare le variabili nell'equazione di Riccati se m=−4k/(2k±1), k∈N, oppure m=−2. Un risultato, questo, che sarà ratificato da Joseph Liouville nel 1841, dimostrando che questi sono tutti e soli i valori di m per i quali l'equazione di Riccati può essere integrata in termini finiti.

Euler inizia a studiare l'equazione di Riccati intorno al 1731 e, riprendendo l'approccio di Jakob I Bernoulli, trova un metodo generale per svilupparne in serie la soluzione, fornendo una costruzione generale, valida anche nei casi in cui non avviene la separazione delle variabili. Più tardi, negli anni 1760-1761, applicando il suo metodo del fattore integrante, esprime l'integrale generale dell'equazione di Riccati tramite la quadratura di un suo integrale particolare e, considerata l'equazione di Riccati generalizzata

[48] dy=R(x)dx+P(x)ydx+Q(x)y²dx,

dimostra che, noti due integrali particolari, l'integrazione di tale equazione si può ricondurre alle quadrature. Euler presenta inoltre negli anni 1762-1763 una nuova dimostrazione per ricavare i valori dell'esponente m per i quali l'equazione è integrabile in termini finiti.

L'equazione di Riccati generalizzata è studiata anche da d'Alembert, come dimostra una lettera inviata a Lagrange nel 1769, in connessione all'equazione differenziale lineare del secondo ordine

da lui ottenuta con il metodo della separazione delle variabili per il problema della corda vibrante di spessore variabile. È noto infatti che a ogni equazione differenziale lineare omogenea del secondo ordine corrisponde un'equazione di Riccati generalizzata e viceversa.

Altre ricerche sulle equazioni differenziali lineari di ordine superiore scaturiscono dagli studi di numerosi problemi fisico-matematici, quali quelli sulla vibrazione di corpi elastici, sulla conduzione del calore, sulla teoria del potenziale, e così via, che conducono appunto a equazioni di questo tipo. Le più semplici equazioni differenziali lineari sono quelle omogenee a coefficienti costanti

che, in alcuni casi particolari, sono risolte da Daniel Bernoulli e d'Alembert, ma la cui soluzione generale si deve a Euler, il quale già negli anni 1739-1741 aveva discusso di questo argomento nella sua corrispondenza con Johann I Bernoulli. Egli pubblica nel 1743 la ben nota soluzione delle equazioni differenziali lineari omogenee di ordine n a coefficienti costanti e stabilisce che l'integrale completo di un'equazione lineare omogenea si ottiene come combinazione lineare di n integrali particolari, che oggi riconosciamo essere linearmente indipendenti, anche se Euler non lo rileva in maniera esplicita. Egli osserva infatti che, con la sostituzione y=e^qx, l'equazione differenziale lineare omogenea si muta nell'equazione, attualmente detta 'caratteristica',

[51] A+Bq+Cq^₂+...+Lq^_n=0;

pertanto, se q è una radice dell'equazione caratteristica, allora y=e^qx è una soluzione dell'equazione differenziale. Egli ottiene inoltre l'espressione delle soluzioni particolari sia nel caso delle radici reali (semplici o multiple) sia nel caso delle radici complesse coniugate.

In una successiva memoria del 1750-1751, Methodus aequationes differentiales altiorum graduum integrandi ulterius promota, Euler affronta le equazioni differenziali lineari non omogenee a coefficienti costanti, trovando un metodo che riconduce il problema dell'integrazione di un'equazione di ordine n all'integrazione di un'equazione di ordine n−1: pertanto, iterando il procedimento, l'equazione di partenza si riduce a un'equazione lineare non omogenea del primo ordine, la cui soluzione generale, come detto, era stata trovata da Leibniz e Jakob I Bernoulli.

Negli anni Sessanta sia d'Alembert sia Lagrange gettano le basi della teoria delle equazioni differenziali lineari a coefficienti non costanti e, con metodi diversi, arrivano alla loro risoluzione. Nel carteggio con Lagrange del 1765, d'Alembert mostra come la conoscenza di n−1 integrali particolari dell'equazione omogenea associata permetta di ridurre l'equazione di partenza a un'equazione non omogenea del primo ordine. Allo stesso risultato giunge Lagrange con un metodo che consiste nel moltiplicare l'equazione per una funzione arbitraria e integrare per parti; in questo modo egli perviene al concetto di equazione aggiunta e alle proprietà di detta equazione, tramite la quale riesce ad abbassare di un'unità l'ordine dell'equazione di partenza. A Lagrange si deve inoltre il celebre metodo della variazione delle costanti arbitrarie, già intuito, come si è visto, da Jakob I Bernoulli nel 1696 per la soluzione dell'equazione che porta il suo nome. Esso permette di determinare una soluzione particolare di un'equazione non omogenea, una volta noto l'integrale generale dell'equazione omogenea associata. L'idea guida è quella di determinare, per esempio nel caso di un'equazione del secondo ordine

due funzioni c1(x) e c2(x) in modo che l'equazione ammetta una soluzione del tipo y(x)=c1(x)y1(x)+c2(x)y2(x), dove y1(x) e y2(x) sono due soluzioni indipendenti dell'equazione omogenea associata.

Le equazioni alle derivate parziali

I primi studi sulle equazioni alle derivate parziali risalgono agli anni Quaranta del XVIII sec., nonostante la nozione di differenziazione parziale fosse già nota nel secolo precedente, ma è soltanto verso la fine del Settecento e i primi anni dell'Ottocento che prende avvio una trattazione sistematica, almeno per ciò che concerne le equazioni alle derivate parziali del primo ordine. La notazione oggi utilizzata per le derivate parziali ∂/∂x,∂/∂y,…, che adotteremo nel seguito, non s'incontra fin dalle origini, ma fu generalmente accettata soltanto nella seconda metà dell'Ottocento.

Euler è il primo a imbattersi in espressioni che si possono interpretare come equazioni alle derivate parziali, precisamente quando, generalizzando i risultati da lui ottenuti sulle funzioni omogenee, si pone il problema di determinare funzioni y=y(x,a) tali che ∂y/∂a soddisfi relazioni del tipo F(x,y,a,∂y/∂x,∂y/∂a)=0. La tecnica risolutiva qui adottata consiste nell'eliminare ∂y/∂a dall'equazione e dall'espressione del differenziale totale e nell'utilizzare opportuni fattori integranti per ricondursi a un'equazione differenziale esatta. La finalità insita nell'articolo di Euler non è però l'integrazione delle equazioni alle derivate parziali, bensì il problema studiato, per cui questo lavoro, come osserva Demidov (1982a), non si può ancora considerare l'origine della teoria di tale tipo di equazioni differenziali.

È d'Alembert che, affrontando problemi di fisica matematica, in particolare quelli sulle vibrazioni della corda, sente la necessità di considerare le equazioni alle derivate parziali come oggetto di studio in sé e di elaborare metodi per la loro risoluzione. Per questo motivo concordiamo con Demidov nel considerare d'Alembert il fondatore della teoria di questa famiglia di equazioni, non soltanto perché ha trovato le soluzioni di alcune equazioni alle derivate parziali del secondo ordine, fra cui quella della corda vibrante, e ha ideato alcuni importanti metodi di risoluzione, ma anche perché ha dato contributi alla risoluzione delle equazioni del primo ordine e l'avvio alla nascita del concetto di soluzione classica o regolare per un'equazione di tale tipo.

Nella prima edizione del Traité de dynamique (1743) il problema delle piccole vibrazioni di una corda pesante, di lunghezza l, sospesa a un estremo è ricondotto all'equazione

ossia

in cui p=∂y/∂t e q=∂y/∂x , equazione che d'Alembert non è ancora in grado di risolvere. Pochi anni dopo egli elabora un metodo per le equazioni alle derivate parziali del secondo ordine, che applica poi ad alcuni problemi specifici; d'Alembert considera le espressioni differenziali

[55] α(u,x)dx+β(u,x)du,

[56] ϱα(u,x)du+νβ(u,x)dx+A(u,x)du+Γ(u,x)dx

(dove le costanti ϱ e ν e le funzioni Α e Γ sono assegnate), che rappresentano il differenziale totale di due funzioni incognite z(u,x) e w(u,x), e, applicando la condizione di Clairaut-Euler vista poc'anzi, deduce il sistema di equazioni

che, in termini delle derivate parziali seconde delle funzioni z e w, può essere espresso nella forma più significativa (non utilizzata però da d'Alembert):

Egli manipola poi le espressioni differenziali di partenza in modo da ottenere loro combinazioni lineari, i cui coefficienti sono numeri o funzioni, e opera su queste con opportuni cambiamenti delle coordinate e delle funzioni incognite, allo scopo di pervenire a espressioni integrabili in virtù della condizione di esattezza delle forme differenziali. Tale procedimento è applicato ad alcuni problemi specifici.

Nello stesso anno, il 1747, d'Alembert presenta alla Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino due importanti memorie, Recherches sur la courbe e Suite des recherches sur la courbe, in cui fornisce la soluzione del celebre problema della corda vibrante, su cui tutti i più eminenti matematici si cimentano, per il rilievo che esso aveva assunto in fisica e nella teoria della musica. Il problema delle piccole vibrazioni di una corda tesa lungo l'asse x si traduce nello studio dell'equazione alle derivate parziali del secondo ordine

in cui k è costante e y(x,t) rappresenta la deviazione, al tempo t, del punto x dalla sua posizione di riposo. L'equazione della corda vibrante viene scritta da d'Alembert nella forma

in cui p=∂y/∂t e q=∂y/∂x , e applicando il suo metodo giunge alla soluzione

[61] y(x,t)=Ψ(kt +x)+ Γ(kt -x),

dove Ψ e Γ sono funzioni arbitrarie di una variabile. Nella prima memoria d'Alembert considera il caso k²=1 e nella seconda k²≠1. In quest'ultima egli inoltre affronta, per la corda di lunghezza l, il problema con le condizioni iniziali

e le condizioni agli estremi

[63] y(0,t)=y(l,t)0

e ottiene la soluzione

[64] y(x,t)=Ψ(kt +x)-Ψ(kt-x),

dove Ψ è una funzione periodica di periodo 2l tale che

[65] Ψ(x)-Ψ(-x)=f(x)

e

In questa stessa memoria, a proposito dello studio delle vibrazioni di una corda fissata agli estremi, la cui configurazione iniziale sia una retta oppure una sinusoide, troviamo le origini del metodo della separazione delle variabili; d'Alembert osserva infatti che la soluzione y(x,t) può essere scritta come prodotto di due funzioni, l'una della variabile x e l'altra della variabile t

[67] y(x,t)=S(x)T(t)

In una successiva memoria, edita nel 1752, egli esplicita questa osservazione e, partendo dall'uguaglianza

[68] ψ(t+x)-ψ(t-x)=S(x)T(t),

determina, senza servirsi dell'equazione differenziale che rappresenta il problema, le funzioni S e T. Nel 1758 il metodo della separazione delle variabili è utilizzato, operando direttamente sull'equazione, per risolvere quella particolare equazione alle derivate parziali, relativa alle vibrazioni di una corda sospesa a un estremo, che d'Alembert non sapeva trattare nel 1743. Nella seconda edizione del Traité de dynamique (1758), infatti, egli cerca la soluzione dell'equazione

dove p=∂y/∂t e q=∂y/∂x, nella forma S(x)T(t); sostituendo nell'equazione differenziale trova le equazioni lineari ordinarie

ove n è costante. Più tardi, come si è già detto, d'Alembert applica l'idea della separazione delle variabili allo studio delle vibrazioni di una corda di spessore variabile. Considerata l'equazione

egli cerca soluzioni della forma

ottenendo per ζ l'equazione ordinaria

Negli anni 1748-1761 si sviluppa fra Euler e d'Alembert un acceso dibattito sulle proprietà di regolarità della soluzione del problema della corda vibrante, che pone l'accento sul concetto di soluzione di un'equazione alle derivate parziali, e si vedono affiorare negli scritti dei due autori le nozioni di soluzione debole e di soluzione classica. Le discussioni sul problema delle piccole vibrazioni della corda coinvolgono in questo periodo, e negli anni immediatamente successivi, i più eminenti matematici dell'epoca e sollevano importanti questioni circa il concetto di funzione e la rappresentabilità di una funzione tramite serie trigonometriche. Già nel 1713 Taylor aveva dato la schematizzazione fisica e geometrica del problema studiando le vibrazioni di una corda di lunghezza l fissata agli estremi e aveva osservato che in ogni istante essa assume la forma sinusoidale

Daniel Bernoulli, basandosi su questa osservazione e su considerazioni puramente fisiche, senza far ricorso all'equazione [59], nel 1753 aveva asserito che la soluzione del problema poteva essere rappresentata sempre nella forma (oggi nota come 'serie di Fourier'):

dove le a_n sono costanti opportune. Bernoulli giustificava tale risultato osservando che i successivi valori di n (cioè n=2, 3,…) dovevano corrispondere alle successive armoniche di una corda vibrante, cioè a suoni che effettivamente la corda può dare simultaneamente al suono fondamentale (n=1). L'asserzione di Bernoulli pone a Euler e d'Alembert, che partendo dalla [59] hanno anch'essi ottenuto soluzioni espresse in termini di serie trigonometriche, l'interrogativo se tutti i moti possibili della corda possano essere rappresentati nella forma [76]. Essi concludono che ciò avviene soltanto in alcuni casi particolari, cioè quando la configurazione iniziale della corda si può esprimere nella forma

il che non è possibile, secondo loro, per una funzione qualunque. La chiarificazione e precisazione del concetto di funzione e della rappresentabilità di una funzione tramite serie trigonometriche avverrà soltanto nel corso dell'Ottocento, per merito soprattutto di Cauchy e di Jean-Baptiste-Joseph Fourier (1768-1830).

Gli studi successivi sulle equazioni alle derivate parziali del secondo ordine non seguono più la via di cercare di ricondursi a differenziali totali, ma approfondiscono il metodo della separazione delle variabili e quello delle coordinate caratteristiche. Euler, per esempio, utilizza questi metodi per trattare problemi matematici o fisico-matematici, quali l'equazione delle onde generalizzata, la propagazione del suono, le piccole vibrazioni di una corda pesante sospesa verticalmente, oppure di una membrana elastica rettangolare e, in quest'ultimo caso, ricava l'equazione delle onde in due coordinate spaziali.

A questo stadio gli sforzi degli studiosi sono ancora concentrati nella risoluzione di equazioni del secondo ordine di tipo iperbolico, mentre per le equazioni di tipo ellittico e parabolico occorre arrivare alla fine del Settecento (per l'equazione di Laplace) e agli inizi dell'Ottocento (per l'equazione del calore).

Euler si era imbattuto nell'equazione del potenziale, oggi detta 'equazione di Laplace',

in occasione dei suoi studi sulla meccanica dei fluidi, ma si era limitato a considerare casi particolari in cui S è un polinomio. Va appunto a Laplace il merito di aver attirato l'attenzione dei matematici sull'equazione che oggi porta il suo nome e che è alla base della teoria del potenziale. Nella celebre memoria del 1782, Théorie des attractions des sphéroides et de la figure des planètes, e in quella del 1787, Mémoire sur la théorie de l'anneau de Saturne, Laplace determina infatti l'equazione che deve essere soddisfatta dal potenziale V della forza esercitata da uno sferoide su un punto esterno, sia in coordinate sferiche:

sia in coordinate cartesiane ortogonali,

Anche se, come si è detto, le maggiori energie furono rivolte alle equazioni del secondo ordine per il rilievo che esse hanno nella soluzione dei problemi della fisica matematica, gli studiosi del XVIII sec. non trascurarono le ricerche sulle equazioni del primo ordine. Fra il 1760 e il 1770, stimolato dagli scritti di d'Alembert, Euler elabora metodi per la risoluzione delle equazioni alle derivate parziali del primo ordine e li applica a problemi particolari, ottenendo un gran numero di risultati interessanti, in seguito raccolti in modo sistematico e generale nel terzo volume delle Institutiones calculi integralis (1768-1770). Nella sua trattazione egli mostra che una famiglia di funzioni z=f(x,y,a,b), ove a e b sono parametri, verifica l'equazione

[81] F(x,y,z,p,q) = 0,

dove p=∂z/∂x e q=∂z/∂y, che si ottiene eliminando a e b fra le espressioni di z, p, q e osserva che, viceversa, la soluzione di tale equazione dipende da una funzione arbitraria. L'idea guida del metodo di Euler consiste nel ricondursi, tramite vari artifici, a differenziali totali e nell'integrare le espressioni differenziali ottenute per mezzo di opportuni fattori integranti. Euler interpreta tutte le variabili come variabili indipendenti, senza privilegiare le variabili spaziali x e y, e ciò gli permette di semplificare le sue procedure scegliendo le variabili in modo opportuno.

Nel 1768 d'Alembert pubblica una memoria che si può considerare conclusiva di tutti i suoi contributi, in quanto include i metodi da lui applicati alla risoluzione di equazioni alle derivate parziali sia del primo ordine, sia di ordine superiore.

Sulla base dei risultati di Euler e d'Alembert, Laplace presenta nel 1773 all'Académie Royale des Sciences di Parigi uno studio sull'integrazione delle equazioni alle derivate parziali nel quale espone un proprio metodo per risolvere l'equazione:

Un contributo fondamentale alla teoria delle equazioni alle derivate parziali del primo ordine è offerto da Lagrange il quale, nella memoria Sur l'intégration des équations à différences partielles du premier ordre (1772), affronta il problema di stabilire quando una soluzione debba essere considerata completa. Euler nelle Institutiones calculi integralis aveva asserito che un integrale di un'equazione alle derivate parziali di ordine n è completo quando dipende da n funzioni arbitrarie; Lagrange invece distingue qui fra soluzione completa e soluzione generale. Completa è una famiglia di soluzioni F(x,y,z,a,b)=0 che dipende da due parametri a e b. Se si pone b=φ(a), dove φ è una funzione arbitraria, si ricava una famiglia di soluzioni F(x,y,z,a,φ(a))=0 dipendenti da un solo parametro. L'insieme di soluzioni che si ottengono risolvendo il sistema

e che rappresentano gli inviluppi della precedente famiglia a un parametro è la soluzione generale, dal momento che dipende da una funzione arbitraria. Lagrange infine denomina "integrale particolare" (oggi soluzione singolare) la soluzione che si ottiene eliminando sia a sia b dal sistema

e che è l'inviluppo della famiglia di superficie soluzione completa. Con questi nuovi concetti Lagrange affronta lo studio delle equazioni alle derivate parziali non lineari del primo ordine, del tipo

[85] q=f (x,y,z,p),

e cerca di determinare p in termini delle variabili x, y, z in modo che, moltiplicando per un fattore integrante ("moltiplicatore") M(x,y,z), la forma differenziale dz−pdx−qdy diventi esatta e dunque l'equazione differenziale dz−pdx−qdy=0 sia integrabile. Lagrange osserva che se si conosce una funzione g(x,y,z,a), dove a è un parametro, tale che l'equazione differenziale

[86] g(x,y,z,a)dx+f(x,y,z,g(x,y,z,a))dy = 0

ammetta una soluzione del tipo F(x,y,z,a)−b=0, questa soluzione è una soluzione completa. Egli utilizza poi la condizione di Clairaut per l'esistenza di un fattore integrante e ottiene un'equazione lineare nelle derivate parziali della funzione g:

ove R, S, T e U sono le forme

In tal modo il problema di risolvere l'equazione non lineare [85] è ricondotto al problema di risolvere l'equazione lineare [87]. Solo in una memoria del 1779 Lagrange mostra come si ottiene la soluzione di un'equazione lineare nelle derivate parziali della funzione incognita z=z(x₁,x₂,...,x_n),

facendo vedere che essa si può ricondurre al sistema di equazioni ordinarie

Egli però stranamente non rileva che a questo punto ha dimostrato che la generica equazione alle derivate parziali del primo ordine [85] è riconducibile a un sistema di equazioni ordinarie e ancora nel 1785, a proposito di un'equazione di questo tipo, afferma che non è risolubile con i metodi conosciuti. Si deve a Paul Charpit (m. 1784) l'osservazione esplicita che i metodi ideati da Lagrange per risolvere le equazioni non lineari e le equazioni ordinarie lineari permettono di trovare la soluzione della generica equazione alle derivate parziali del primo ordine.

Una proficua interpretazione geometrica degli integrali della [87] è data da Gaspard Monge (1746-1818), che tra il 1784 e il 1795 introduce un concetto analogo a quello che oggi chiamiamo varietà caratteristica. Si apre così la via a una teoria geometrica delle equazioni differenziali che sarà ampiamente sviluppata nel secolo successivo. Accanto a questa proseguiranno le ricerche sui metodi più convenienti per risolvere specifiche classi di equazioni alle derivate parziali. Tuttavia, con gli anni Venti dell'Ottocento il punto di vista teorico si sposterà e inizierà una nuova epoca per gli studi sulle equazioni differenziali: la considerazione dei problemi con condizioni iniziali o al contorno concentrerà l'attenzione sugli integrali particolari, a scapito dell'integrale generale o completo, e la ricerca di teoremi di esistenza, di unicità e, più tardi, di regolarità delle soluzioni di questi problemi diverrà la questione centrale della teoria.