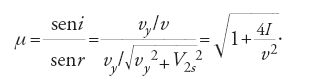L'Età dei Lumi: l'avvento delle scienze della Natura 1770-1830. La fisica matematica

L'Eta dei Lumi: l'avvento delle scienze della Natura 1770-1830. La fisica matematica

La fisica matematica

1. Definizioni e ambito

L'oggetto della fisica matematica, nel periodo che va dal 1770 al 1830, ossia da poco prima del crollo dell'Ancien Régime alla fine della monarchia della restaurazione in Francia, può essere definito in vari modi. Due considerazioni principali hanno orientato la scelta operata in questo capitolo. La prima è che durante il XVIII sec. l'ambito e i metodi della 'fisica' mutarono drasticamente. Se agli inizi del secolo la fisica era uno studio teorico e qualitativo dell'intero mondo naturale, alla fine del Settecento essa si trasformò in un'indagine sperimentale e semiquantitativa del comportamento macroscopico della materia inorganica; questo nuovo approccio escludeva non soltanto la storia naturale, ma anche i particolari della chimica. Ovviamente sopravvissero tracce delle vecchie abitudini; ancora nel 1784 Franz Karl Achard (1753-1821), membro di primo piano della Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino e convinto fautore della quantificazione nelle scienze fisiche, indicava l'agricoltura come uno dei "più interessanti settori della fisica".

La fisica, perseguendo la quantificazione, incorporò parti della meccanica analitica, dell'astronomia e dell'ottica. Gli autori dei testi di fisica inserirono questa nuova acquisizione nell'ambito di una struttura tradizionale che distingueva fra la physica generalis, che trattava delle proprietà più comuni dei corpi, come la coesione, l'inerzia, il peso e la gravitazione, e la physica particularis, che includeva al suo interno soggetti particolari, come la luce, il magnetismo, la meteorologia e la chimica generale. Di seguito ci limiteremo a presentare alcuni esempi rappresentativi della physica generalis, in modo da dare un'idea delle parti meno tecniche della materia; tali esempi sono stati scelti perché rivestono un interesse generale, oppure perché sono strettamente correlati con i rami della physica particularis che tratteremo in dettaglio.

Nell'ambito della physica particularis dedicheremo un'attenzione speciale a quei settori che fra il 1770 e il 1830 sono stati dominati dalla teoria degli imponderabili. Questi settori sono stati resi parti integranti di una visione unitaria da una diffusa impostazione metodologica, da un'interpretazione strumentalistica e da un insieme di analogie reciprocamente interconnesse; essi facevano comune riferimento a fluidi ipotetici privi di peso, veicoli delle forze agenti a distanza, che si supponeva causassero i fenomeni della luce, del calore, dell'elettricità e del magnetismo.

Secondo Jean-Baptiste Biot (1774-1862), che nel 1816 pubblicò il primo manuale di 'fisica sperimentale e matematica' del mondo, erano questi i settori trainanti della fisica matematica di quel periodo; com'egli afferma nel Traité de physique expérimentale et mathématique (1816), nei quarant'anni precedenti la fisica aveva perfezionato la termometria e la barometria, aveva inventato l'igrometria, aveva scoperto le leggi di dilatazione della materia, della formazione dei gas, dell'elasticità e della torsione e aveva spiegato la capillarità e la velocità del suono. Tutto ciò era encomiabile, ma i contributi fondamentali alla fisica riguardavano gli agenti dell'elettricità, del magnetismo e del calore: "Quali non sono i progressi compiuti nello studio di questi principî invisibili, intangibili e imponderabili!" (Traité de physique, I, p. 111 e segg.).

La seconda considerazione che influisce sul contenuto di questo campo è che la misurazione esatta può essere qualificata come fisica matematica anche qualora non sia legata a una teoria di tipo quantitativo. Biot attribuì una posizione preminente alla misurazione esatta e non alla teoria quantitativa, poiché riteneva che un dato errato potesse orientare i teorici in una direzione sbagliata, mentre una teoria errata poteva essere facilmente eliminata da una misura corretta.

Nell'attività pratica di ricerca della scuola francese le teorie potevano essere così sofisticate dal punto di vista matematico da far sì che, in un primo tempo, nessuna misurazione potesse confermare i loro 'ingredienti'. Questo aspetto della teoria degli imponderabili irritava i filosofi sperimentali inglesi, per i quali la locuzione stessa di 'fisica matematica' designava un concetto straniero; l'antipatia derivava in parte da una loro relativa debolezza in matematica, ma si basava anche su un punto di forza, ossia sulla percezione del fatto che le teorie quantitative troppo elaborate potevano occultare il meccanismo reale dei fenomeni. Thomas Young (1773-1829), anch'egli brillante esponente della fisica quantitativa, nel 1809 espresse in questi termini il punto di vista inglese: "I primi matematici del continente hanno dimostrato una grande ingegnosità nell'immergere le verità più chiare della meccanica nei labirinti delle formule algebriche, e in alcuni casi hanno finito per perdere di vista lo stato effettivo della ricerca, occupandosi soltanto dei simboli usati nel rappresentare i suoi passi intermedi" (Frankel 1974, pp. 242-243). Questa critica infastidì Biot. Egli ammise che i suoi compatrioti avevano forse troppa fretta di calcolare, ma insisteva sul fatto che era ragionevole rappresentare con leggi quantitative solamente il comportamento di un fenomeno studiato a sufficienza e con precisione; questo era il metodo di Newton e costituiva il corpo e l'anima della fisica.

Nei paragrafi che seguono descriveremo brevemente l'avvicinamento della fisica alla matematica, accenneremo all'epistemologia della fisica matematica, offriremo alcuni esempi di physica generalis e, muovendoci verso la physica particularis, daremo, infine, una descrizione del sistema degli imponderabili.

2. Le radici e la retorica

L'affermazione secondo la quale la filosofia naturale era fondata sulla matematica iniziò a corrispondere alla realtà intorno al 1770, e ciò in seguito a uno sviluppo che presentava un triplice aspetto. In primo luogo, l'ambito della filosofia naturale fu sempre più definito dalla fisica sperimentale; in secondo luogo, la fisica sperimentale abbandonò gradualmente le dimostrazioni e le indagini di tipo qualitativo a favore delle misurazioni effettuate con strumenti sempre più precisi; in terzo luogo, la filosofia naturale costruì nuovi edifici con i rami che potava dal grande albero della matematica applicata. In tal modo essa prefigurò quel miscuglio di esperimenti sistematici, misurazioni precise e teorie quantitative che avrebbe caratterizzato gran parte della fisica degli ultimi duecento anni.

Il processo di quantificazione della filosofia naturale che ebbe luogo nei decenni intorno al 1800 era stato preparato, dal punto di vista retorico e programmatico, nel corso di un intero secolo. Per citare un esempio noto, Bernard Le Bovier de Fontenelle (1657-1757), che fu per quarant'anni segretario perpetuo dell'Académie Royale des Sciences di Parigi, scrisse nella Préface de l'histoire de l'Académie des Sciences (1730), verso la fine del suo mandato, che "la fisica ha sostanza soltanto per quel tanto che è fondata sulla geometria" (ed. 1825, I, p. 15). Tuttavia, la maggior parte della fisica che egli diede alle stampe in veste di curatore dei "Mémoires" dell'Académie di Parigi era interamente qualitativa. Nel suo ruolo di curatore, Fontenelle definiva la 'fisica' come l'insieme delle materie, di natura qualitativa, che formavano la classe di fisica dell'Académie, ossia l'anatomia, la chimica e la botanica.

I rivali degli accademici francesi, i membri della Royal Society di Londra, caddero nel 1718 in una contraddizione dello stesso tipo: pubblicarono infatti un elenco in cui figuravano i loro nomi seguiti dall'indicazione dei rispettivi interessi di scienza. Quasi la metà di coloro che dichiararono una preferenza (circa 25) indicò la matematica e la 'filosofia naturale', anche se nessuno di loro si occupava di queste due discipline, in quanto essi s'identificavano semplicemente con l'oggetto delle ricerche di Newton. Allo stesso modo, il chimico olandese Herman Boerhaave (1668-1738) affermò, in un noto discorso del 1715, che la matematica offriva l'unica vera via per la generalizzazione nella scienza, via che però egli stesso non seguì quando dovette generalizzare. Per restare più vicini all'oggetto della nostra trattazione, Willem Jacob 'sGravesande (1688-1742), collega di Boerhaave all'Università di Leida, considerava la fisica un ramo della matematica e redasse la prima esposizione di buon livello della filosofia naturale di Newton; eppure nel suo libro non vi è traccia di matematica.

Mezzo secolo più tardi, i 'quantificatori' della fisica mettevano in pratica ciò che predicavano. Johann Heinrich Lambert (1728-1777) nel 1765, quando fu nominato membro dell'Accademia delle Scienze di Berlino, dichiarò che effettuare esperimenti senza calcolare era come agire senza pensare, vale a dire, come puntualizzò il suo giovane collega Achard nel Mémoire sur la mesure de la force de l'électricité (1782), semplicemente equivaleva a giocare: "La storia della fisica dimostra una verità ormai abbastanza riconosciuta: il filosofo naturale che non misura sta soltanto giocando, e differisce dal bambino soltanto per la natura del suo gioco e le caratteristiche costruttive dei suoi giocattoli" (p. 196). Lambert aveva la mania di quantificare qualsiasi cosa, dalla fisica alla metafisica, e Achard stava ininterrottamente per giorni e notti nel suo laboratorio (una volta vi trascorse tredici giorni) per ottenere misure di quantità fisiche fino a quattro cifre significative.

Il modo in cui l'Académie Royale des Sciences di Parigi fu riorganizzata nel 1785 rappresenta pienamente la nuova importanza che le misurazioni avevano assunto nella fisica. Quell'anno furono aggiunte due nuove sottoclassi: quella di fisica sperimentale e quella di storia naturale e meteorologia. La prima rientrava nella classe di matematica e indicava chiaramente il moderno modo d'intendere la fisica, ossia una scienza quantificata o quantificabile; la seconda fu inserita nella classe di fisica, al fine di mantenere gli equilibri dell'Académie e, al tempo stesso, il vecchio significato della fisica come studio qualitativo del mondo naturale. Nel 1807 anche l'Accademia Reale delle Scienze di Amsterdam subì una riorganizzazione di questo tipo.

Come queste vicende istituzionali possono suggerire, la spinta verso la quantificazione della fisica provenne non dalla teorizzazione matematica ma dalla misurazione esatta. In questo contesto la crescente precisione e capacità degli strumenti, entrambe in continua espansione, giocarono un ruolo determinante. Nel XVIII sec. l'esempio tipico di scienza quantitativa era l'astronomia; dal 1700 al 1800 la precisione dei telescopi aumentò di un fattore 100, e ciò rese possibile osservare fenomeni di piccola entità, come l'aberrazione stellare, la nutazione della Terra e la variazione secolare dell'obliquità dell'eclittica. Negli anni Settanta e Ottanta del secolo i principali strumenti meteorologici, cioè il barometro e il termometro, migliorarono quasi fino a raggiungere i livelli di quelli astronomici, e gli elettrometri divennero tanto affidabili da permettere la definizione delle grandezze elettrostatiche e lo studio delle loro relazioni quantitative. Anche strumenti meccanici come, per esempio, le bilance, subirono notevoli perfezionamenti che resero possibile il moltiplicarsi delle misure della spinta di Archimede, delle tensioni superficiali e dei pesi specifici, con un numero di cifre significative a volte eccessivo.

Tra il 1801 e il 1808 Johann Carl Fischer (1761-1833), lettore di matematica nell'Università di Jena, pubblicò una Geschichte der Physik in otto volumi e 7.500 pagine. Egli suddivise il periodo moderno, da Newton fino al tempo in cui egli scriveva, in due parti, la seconda delle quali aveva inizio intorno al 1770 con la scoperta dei differenti tipi di gas. Nel caso ‒ piuttosto rappresentativo ‒ del calore, a Fischer servirono quattro tabelle per riportare i dati accumulati nel primo periodo e sedici per quelli del secondo; se si considera che quest'ultimo copre un arco temporale di appena la metà del primo, ciò implica un incremento di otto volte. Quando le tabelle riportano gli stessi dati per i due periodi, la precisione del secondo è assai superiore; per esempio, le temperature arrivano a un decimo di grado nel primo e a un millesimo di grado nell'altro; le cifre significative dei coefficienti di espansione sono tre o quattro nel primo e arrivano fino a sei nel secondo.

Un altro indicatore della quantificazione della fisica sono i libri di testo. Bastano alcuni passaggi di un esempio anche poco felice come la Introduction to natural philosophy di William Nicholson (1753-1815) per confermare il quadro dipinto da Fischer. Nella prima edizione del 1782 l'autore discute l'altezza dell'atmosfera da un punto di vista qualitativo; nella quinta edizione, del 1805, dedica all'argomento due tabelle e una pagina di calcoli logaritmici. I testi francesi mostrano una tendenza ancor più netta in questa direzione. Il Traité élémentaire de physique (1803) di René-Just Haüy (1743-1822) fa uso dell'algebra, fornisce dati numerici, ma non utilizza tabelle. Per raggiungere un livello più elevato, Biot rielaborò un libro scritto da Ernst Gottfried Fischer (1754-1831), un professore di ginnasio di Berlino, e lo pubblicò come Physique mécanique nel 1806; la quarta edizione (1830) di questo testo, che mantiene l'organizzazione dell'originale, contiene 23 tabelle, molte delle quali riportano dati con sei cifre decimali. Il grande Traité di Biot del 1816 contiene un numero incalcolabile di tabelle e di dati numerici, e il Précis élémentaire de physique expérimentale (1817), che egli trasse dal Traité per gli studenti di medicina e storia naturale, contiene 49 tabelle, con un numero di cifre decimali variabile da uno a nove, nonostante sotto ogni altro aspetto mancasse di "tutto ciò che rende [la fisica] utile e sicura, ossia dei metodi matematici e delle formule" (Précis, I, p. VI).

Anche i libri di testo indicano l'entità del trasferimento dei rami della matematica applicata nell'ambito della fisica, pur conservando argomenti che ora farebbero parte della chimica. Se ci soffermiamo dapprima su quest'ultimo aspetto, va osservato che il nuovo campo della pneumatica, che J.C. Fischer scelse come principale punto di rottura nella sua periodizzazione della fisica moderna, diede luogo a una sovrapposizione fra la nuova chimica e la nuova fisica. Gli autori dei testi di fisica non lo potevano ignorare. Haüy nel suo Traité élémentaire de physique dichiara che "il vero fisico (physicien) parla il linguaggio della chimica" (ed. 1806, I, p. II-III). La Physique mécanique di Fischer e Biot divideva i lettori in physiciens mécanistes (coloro che ritengono che il calore sia un movimento) e physiciens chimistes (coloro che credono che sia una sostanza), e tutte le edizioni dell'Introduction di Nicholson includevano i principî della pneumatica come un argomento scontato.

Intorno al 1800 le pretese degli autori dei libri di testo e di altri scrittori di fisica nei confronti d'interi settori della matematica applicata divennero insistenti e in alcuni casi addirittura imperialistiche. Il Physikalisches Wörterbuch (Dizionario di fisica) di Johann Samuel Traugott Gehler (1751-1795), pubblicato tra il 1787 e il 1796, si proponeva di annettere al suo interno l'intera disciplina. Il dizionario rivale di J.C. Fischer, che recava lo stesso titolo Physikalisches Wörterbuch (1798-1827), considerava la fisica come costituita dalle "parti scelte" della matematica applicata, con l'aggiunta, più recente, degli argomenti più importanti della chimica.

Possiamo datare con precisione il momento in cui gli autori di libri di testo tedeschi riconobbero la necessità della quantificazione della fisica. Friedrich Albrecht Carl Gren (1760-1798), professore di fisica e chimica all'Università di Halle e fondatore del "Journal der Physik", era stato educato alla vecchia concezione della fisica, qualitativa e onnicomprensiva. Negli anni Novanta del Settecento si rese conto della necessità d'inserire alcuni numeri nei suoi testi di fisica per renderli competitivi; pur trovandosi impreparato di fronte a questa improvvisa esigenza, fece del suo meglio per fronteggiarla e s'immerse nello studio della matematica. Purtroppo aveva atteso troppo a lungo; nonostante il suo zelo, "i suoi lavori di matematica mostravano come non si sentisse completamente a suo agio con il rigore dell'argomentazione matematica" (Grundriss der Naturlehre, ed. 1808, p. XV).

Si può lasciare l'ultima parola su questo argomento a Jean-Henri Hassenfratz (1755-1827), il primo professore di fisica dell'École Polytechnique, istituzione fondata nella Francia rivoluzionaria. Nella relazione Physique générale: de l'enseignement de cette science, il testo della quale fu pubblicato sul "Journal de l'École Polytechnique" nel 1799, Hassenfratz attribuì i recenti progressi nella conoscenza della Natura a "un metodo di sperimentazione rigoroso e pressoché matematico"; ci si poteva aspettare molto dall'"unione di geometri e savants", in particolare l'unione in un unico corpo, quello del polytechnicien modello, del physicien completo, araldo della fisica classica, che si trova perfettamente a suo agio sia nelle misurazioni di laboratorio sia nei calcoli a tavolino (p. 372).

3. Lo strumentalismo e gli imponderabili

Il mondo del 'come se'

Una descrizione matematica del mondo presentava il vantaggio di non dover essere presa alla lettera. Era possibile alterare un termine, un coefficiente, un parametro, o persino un'equazione o un modello senza che fosse necessario modificare la visione del mondo. Dopo la condanna di Galilei, i gesuiti avevano sfruttato questa opportunità, calcolando secondo il modello eliocentrico e predicando quello geocentrico; i filosofi naturali della fine del XVIII sec. adottarono una tattica e una retorica di questo tipo. Il loro scopo non era tanto quello di evitare la censura della Chiesa, quanto quello di evitare il loro stesso scetticismo; essi potevano quindi misurare senza sbilanciarsi sull'esistenza delle entità che comparivano nelle loro teorie. Questa situazione è ben rappresentata dall'ossimoro 'pesare gli imponderabili'; dato che, anche se molte delle entità introdotte per rendere possibile la quantificazione erano considerate prive di peso, numerosi strumenti usati per misurare i loro effetti erano bilance.

L'alleanza fra strumenti e strumentalismo fu favorita dalla diffusione delle teorie del marchese di Condorcet (1743-1794) e di Immanuel Kant (1724-1804). La visione di Condorcet, in base alla quale il progresso nella scienza equivale né più né meno che alla costruzione di un linguaggio atto a descrivere i fenomeni naturali, e quella di Kant, per il quale i fenomeni stessi contengono un'inevitabile aggiunta apportata dalla mente che percepisce, insegnarono al filosofo naturale che la conoscenza dei veri principî non può mai essere dimostrata, né è necessario cercarla. Secondo Georg Christoph Lichtenberg (1742-1799), professore di fisica all'Università di Gottinga, lo schema migliore è quello che rende la comprensione più semplice "per quanto possa essere lontano dalla verità cui vogliamo avvicinarci usandolo" (Erxleben, Anfangsgründe der Naturlehre, p. XXV).

I concetti più generali della fisica non potevano sfuggire all'effetto corrosivo di questa forma di 'irrealismo'. Secondo Haüy, l'attrazione e la repulsione non sono agenti, ma fenomeni, ossia "le velocità con le quali i corpi tendono ad avvicinarsi o ad allontanarsi l'uno rispetto all'altro" (Traité élémentaire de physique, ed. 1806, I, p. II). Il calore si prestava particolarmente bene alla retorica irrealista. Haüy esprimeva una preferenza per la teoria materiale rispetto alla perenne alternativa cinetica, seguendo un criterio di convenienza e non di verità. Nicholson insegnava la stessa dottrina nei suoi libri di testo di fisica e di chimica. Biot mise in chiaro che la fisica matematica non può penetrare la natura degli agenti che descrive; le misurazioni precise e una teoria esatta possono soltanto indicare "un modo di esistenza più o meno plausibile" (Traité de physique, I, pp. XVI-XVII).

Questo per quel che riguarda i libri di testo e i dizionari; anche gli scritti di carattere programmatico degli studiosi che svilupparono la teoria del calorico erano pervasi da questo tipo di strumentalismo. La scuola scozzese, che inventò i concetti di calore specifico e calore latente, rinunciò ad affermare l'esistenza oggettiva del materiale 'calore' sul quale essa ragionava; gli esperti ginevrini del calore radiante assunsero la stessa posizione. Gli studiosi francesi che perfezionarono la teoria del calorico, Antoine-Laurent Lavoisier (1743-1794) e Pierre-Simon de Laplace (1749-1827), riconobbero che anche la rivale teoria cinetica poteva spiegare tutti i loro risultati. Leggiamo nel Dictionnaire raisonné de la physique (1781) di Mathurin-Jacques Brisson (1723-1806) che la teoria del calorico dovrebbe essere preferita a quella cinetica non perché sia più vera, ma perché è di gran lunga il modo più semplice per spiegare il calore dei corpi.

A suggerire una concezione di tipo irrealista dello schema degli imponderabili contribuì la constatazione che tale schema non poteva essere posto in una forma univoca. I migliori teorici non furono in grado di decidere, in un caso particolarmente esemplificativo, se l'elettricità consistesse in uno o due fluidi. Gli Inglesi rimasero monisti, i Francesi dualisti. Il più grande elettrologo dell'epoca, Alessandro Volta (1745-1827), nonostante preferisse il punto di vista inglese a quello francese "compì le sue scoperte più brillanti supponendo l'esistenza di atmosfere elettriche, alle quali nessuno dei due punti di vista concedeva la minima realtà" (Biot, Traité de physique, I, p. 11).

Anche gli altri principali imponderabili furono soggetti alla stesso scetticismo. Di quanti fluidi magnetici aveva bisogno la teoria? Secondo Franz Ulrich Theodosius Aepinus (1724-1802) di uno, secondo Charles-Augustin Coulomb (1736-1806) di due. "A mio avviso", scrisse J.C. Fischer "non dovremmo condannare l'assunzione di una o di due materie magnetiche, purché essa sia considerata una mera finzione scientifica, concepita per guidare gli esperimenti e le osservazioni, ma non come fondamento delle spiegazioni e delle ipotesi" (Physikalisches Wörterbuch, III, p. 452). Il calore e la luce ponevano la stessa domanda: erano una o due forme di materia? Fischer pensava che la maggioranza fosse incline a considerarli identici, ma le maggiori autorità scientifiche, inclusi Biot, Gren, E.G. Fischer e Haüy, li trattavano come oggetti diversi. Lavoisier aveva messo in questione la loro differenza, eppure nella tabella delle sostanze semplici del Traité élémentaire de chimie (1789) li trattava come ugualmente elementari.

Si può seguire il gioco reciproco fra strumenti e strumentalismo nel più rilevante progetto scientifico della Francia rivoluzionaria. Lo strumento a cui ci riferiamo è il metro, unità fondamentale di lunghezza, definito operativamente come la decimilionesima parte della distanza fra un polo e l'equatore. In questo non sembra esservi alcuna forma d'irrealismo; infatti, la Terra esiste e la distanza in questione era evidentemente misurabile, con il grado di precisione che gli strumenti astronomici e geodetici dell'epoca permettevano. Tuttavia il sistema metrico non rappresentò il primo tentativo di valutare accuratamente la lunghezza di un meridiano di longitudine; gli sforzi precedenti avevano dato luogo a risultati contrastanti, e all'ipotesi scoraggiante, avanzata per la prima volta dal gesuita Ruggero Giuseppe Boscovich (1711-1787), che la Terra potesse non avere una forma definita e regolare da scoprire. L'idea di Boscovich fu assecondata al volgere del secolo dai geodeti britannici, che non vollero investire affatto nella retorica del sistema metrico. Nei primi anni Venti dell'Ottocento il matematico tedesco Carl Friedrich Gauss (1777-1855) si dichiarò favorevole alle idee di Boscovich e inventò il 'geoide', una superficie approssimativamente coincidente con quella media del mare (come se le montagne e le valli non esistessero) e in ogni punto perpendicolare alla direzione della gravità. Questo mondo letteralmente del 'come se' diventava la Terra reale al fine di determinare la sua forma e le sue dimensioni.

Il potere dell'analogia

Gli strumenti della fisica quantitativa intorno al 1800 erano almeno di tre tipi. Il primo, la 'bilancia dinamometrica', misurava la forza, l'energia, l'elasticità o la tensione; ne sono esempi gli elettrometri, le bilance di torsione, i magnetometri, i termometri e i barometri. Un secondo tipo di misuratore fisico era il 'misuratore di quantità', che associava un numero alla quantità di materia o di fluido imponderabile che si supponeva fosse presente; ne sono esempi il calorimetro di Lavoisier e Laplace, il gasometro di Lavoisier e la bilancia comune. Un terzo tipo di strumenti, quello degli 'strumenti indicatori', mostrava la direzione delle forze o dei movimenti, come i rifrattometri e gli indicatori dell'inclinazione e della declinazione magnetica. Descriveremo alcuni di questi strumenti contestualmente alla spiegazione degli esperimenti nei quali essi erano usati.

Le grandezze misurate dalle bilance dinamometriche e dai misuratori di quantità non erano indipendenti. Coloro che usavano gli strumenti interpretavano, per esempio, la lettura di un termometro come la misura della quantità di calore, e anche, o invece, della 'tensione' del calore. La relazione generale fra l'intensità e la quantità di materia imponderabile costituiva un problema importante per i fisici dell'epoca. Tuttavia, verso la fine del secolo, nel caso del fluido elettrico (o dei fluidi elettrici) e del calorico la relazione fra tensione e quantità era stata quantificata con successo grazie all'invenzione di un parametro che caratterizzava le condizioni particolari del corpo nel quale risiedeva l'imponderabile. Basandosi sull'ipotesi immediata che il corpo potesse alterare la tensione, ma non la quantità dell'imponderabile a esso assegnato, il parametro indicava il modo in cui la quantità si manifestava nel corpo che la ospitava. Il primo di questi parametri venne alla luce intorno al 1760 grazie all'opera di Joseph Black (1728-1799), allora professore di chimica all'Università di Glasgow. Riprendendo un vecchio risultato ottenuto da Daniel Gabriel Fahrenheit (1686-1736) ‒ nel caso in cui sono mescolate insieme quantità di mercurio e acqua di uguale peso ma di temperatura diversa, la temperatura della miscela risulta essere sempre più vicina a quella originaria dell'acqua ‒ Black decise che, per subire lo stesso aumento di temperatura, l'acqua poteva assorbire più calore di quanto potesse fare il mercurio; in una parola ‒ quella che usò Black ‒ l'acqua aveva una maggiore 'capacità' per il calore.

Circa vent'anni dopo Johan Carl Wilcke (1732-1796), professore di fisica sperimentale all'Accademia svedese delle Scienze di Stoccolma, lesse un resoconto delle conclusioni di Black, alle quali probabilmente egli era già giunto per suo conto. Wilcke mise in risalto come il concetto di capacità termica specifica consentisse di stabilire un parallelismo fra la teoria dell'elettricità e quella del calore. Volta e altri elettrologi, compreso Wilcke, avevano identificato un parametro che legava la tensione del 'fluido elettrico' indicata da un elettrometro alla carica di un conduttore isolato, determinata in base al numero di rotazioni della macchina elettrica usata per caricarlo; il parametro variava a seconda della forma del conduttore e della sua vicinanza ad altri conduttori. Secondo Wilcke, vi era un perfetto parallelismo fra la capacità per il calore e quella per l'elettricità, e quindi fra la temperatura e la tensione elettrica nonché fra i fluidi calorico ed elettrico.

Non è tutto: Black, Wilcke e Lavoisier, forse in maniera indipendente, si erano resi conto che non tutto il calore immesso in un corpo era indicato da un termometro. Anche in questo caso Black trovò la soluzione per primo, e ancora una volta si giovò di un'osservazione di Fahrenheit. Questi aveva mescolato una certa quantità di acqua calda dapprima con una massa di ghiaccio alla temperatura di fusione e poi con la stessa massa di acqua alla temperatura di congelamento: la temperatura di equilibrio della prima miscela era sempre minore di quella della seconda. Bastava una semplice riflessione per concludere che non avrebbe potuto essere altrimenti, poiché la neve necessita di un certo tempo per sciogliersi, anche alla calda luce del Sole; Black ne dedusse che una certa quantità di calore può essere aggiunta o sottratta ai corpi senza influenzare il termometro, rispetto al quale essa è, per usare la sua espressione, "latente". Wilcke riscoprì il fenomeno e il concetto, e ancora una volta ne mise in rilievo il legame con l'elettricità. Proprio come ogni corpo possiede una certa quantità di elettricità, nel suo stato normale o privo di carica, così ogni corpo, o quantomeno l'acqua, contiene una certa quantità di calore latente che non influenza il termometro. D'altra parte, il calore si manifesta dilatando il mercurio, proprio come un eccesso o un difetto di fluido elettrico, o di fluidi elettrici, al di sopra o al di sotto del livello normale causa il movimento dell'elettrometro.

Lavoisier e Laplace spinsero oltre il parallelismo, lavorando in collaborazione con Volta, che si trovava a Parigi nel momento in cui essi stavano iniziando i loro esperimenti con il calorimetro a ghiaccio. I tre, insieme, cercarono di verificare se durante l'evaporazione si producesse elettrizzazione. Essi si persuasero del fatto che l'acqua in ebollizione produce un fluido elettrico mentre evapora e dimostrarono così "l'analogia fra elettricità e calore" e anche l'antica idea di Lavoisier che "l'elettricità è soltanto un tipo di combustione, nel quale l'aria fornisce la materia elettrica proprio come […] fornisce la materia della luce e del fuoco nella combustione ordinaria" (Guerlac 1976, p. 238). Anche Volta insistette molto sull'analogia impressionante per cui la scienza dell'elettricità fa anche luce sulla teoria del calore; egli si riferiva in particolare al calore latente.

Le analogie fra il calore e l'elettricità possono essere estese alla luce, in base all'idea di Newton che le particelle di luce possono essere combinate con corpi (ed essere quindi in uno stato latente) finché non sono espulse dal riscaldamento o dalla percussione. Così, la fluorescenza rassomigliava alla carica elettrica o al calore manifesto. Il collega più vicino a Laplace, Claude-Louis Berthollet (1748-1822), spinse questo parallelismo fino a trasformarlo in una prova dell'identità di calore e luce. Egli trovò una prova ulteriore di ciò in un gioco di società praticato fin dagli anni Settanta del Settecento, nel quale si giocava con il calore come se si fosse trattato di luce; precisamente, ponendo un carbone ardente nel fuoco di uno specchio metallico, si provocava l'accensione di un combustibile posto nel fuoco di un identico specchio collocato di fronte al primo. Apparentemente il calorico poteva muoversi nell'aria proprio come il fluido elettrico, o i fluidi elettrici, poteva propagarsi sotto forma di scintille; entrambi, inoltre, si propagavano facilmente attraverso i corpi solidi.

A causa di queste analogie i 'fluidi imponderabili' ‒ quali, appunto, i fluidi elettrico, calorico e magnetico ‒ costituirono un sistema che raccolse il consenso della maggior parte dei filosofi naturali nel periodo che va dal 1770 al 1830 circa. Dal punto di vista strumentalista, tale sistema presentava un ulteriore vantaggio, quello di non richiedere una risposta alle domande riguardanti la sua aderenza alla realtà naturale; esso poteva essere emendato oppure ampliato a seconda delle esigenze della crescita della conoscenza, o a seconda dei gusti degli scienziati. Era possibile estendere la coerenza di tale sistema supponendo che le particelle di calore, come quelle dei fluidi elettrici e magnetici, si respingessero a vicenda con una forza che diminuiva in ragione di una potenza intera della distanza. Queste estensioni costituirono la parte più ampia della physica particularis.

4. La 'physica generalis'

Al contrario degli imponderabili, cui si deve il maggiore fervore nella fisica del Settecento, gli argomenti ordinari della physica generalis proseguirono per inerzia lungo i percorsi prefissati. Furono confermate le vecchie teorie e migliorate le vecchie misure, per esempio nello studio della gravitazione universale e della velocità e direzione della caduta libera. Furono estese le relazioni quantitative già note, come nel caso della dimostrazione di una legge di Hooke sulla torsione; ci s'impegnò inoltre nella ricerca di una spiegazione del fenomeno della coesione, vista come effetto di forze a breve raggio d'azione, come nella teoria della capillarità.

La legge universale: la caduta libera

Verso la fine del XVIII sec. due problemi già sollevati da Galilei giunsero a una soluzione pressoché definitiva. Il primo era la misurazione diretta dell'accelerazione di gravità, che Galilei aveva cercato di eseguire usando piani inclinati. Ora esso poteva essere affrontato in maniera adeguata, studiando direttamente la caduta verticale, dopo la pubblicazione, nel 1784, del Treatise on the rectilinear motion and rotation of bodies di George Atwood (1745-1807). L'autore stesso subì però in quell'anno una caduta libera, in quanto da lettore di filosofia naturale a Cambridge passò a far soldi per il tesoro di Londra. La macchina che egli aveva ideato consisteva di una puleggia montata accuratamente e di una corda alla quale erano sospesi dei pesi, che scorreva lungo una scala verticale finemente graduata; un orologio a pendolo di precisione misurava il tempo della caduta. L'apparecchio diede risultati che si accordavano con la legge di Galilei fino a tre o quattro cifre significative, mentre le migliori misurazioni della caduta libera portati a termine da Newton presentavano errori del 20%.

Il secondo problema riguardava un'argomentazione che Galilei aveva utilizzato a proprio vantaggio in modo fin troppo convincente; ci si chiedeva infatti se una palla lasciata cadere da una torre sulla Terra in rotazione cadesse esattamente ai piedi della torre. A nord delle Alpi tale questione suscitava scarso interesse, poiché la rotazione della Terra e tutto il resto del sistema eliocentrico erano stati accettati già da molto tempo; in Italia, invece, dove il Dialogo di Galilei era ufficialmente proscritto (anche se non in pratica), i filosofi naturali erano entusiasti di seguire ogni traccia che promettesse di sostenere o corroborare l'eliocentrismo. Quando, subito dopo la metà del Settecento, Benedetto XIV annullò la condanna delle opere di Copernico nell'Indice dei libri proibiti, il papa stimolò la ricerca di una conferma definitiva delle dottrine di Galilei.

Giovanni Battista Guglielmini (1763-1817) accettò la sfida. Usufruendo della sinecura di tutore matematico presso il Segretariato di Stato del papa, sviluppò la vecchia idea di dimostrare il movimento diurno della Terra misurando lo spostamento verso est rispetto al piede della verticale del punto in cui cade un peso gettato da una torre di una certa altezza. A causa della rotazione, la velocità della cima della torre è più grande di quella della base, e quindi il peso avrebbe dovuto toccare terra ai piedi della torre in un punto leggermente spostato verso est, in misura proporzionale al tempo di caduta. Tutto ciò di cui Guglielmini aveva bisogno era una grande altezza; per tale motivo chiese al suo cardinale il permesso di far cadere delle sfere dalla cupola di San Pietro nel Santo Sepolcro, sito alla base dell'altare del Bernini. Si trattava senza dubbio di un luogo perfetto per discolpare Galilei. Il cardinale accettò. Mentre Guglielmini si domandava perché nessuno, in apparenza nemmeno l'onnisciente Newton, avesse tentato questo semplice esperimento, il cardinale perse il posto; Guglielmini trasferì dunque il suo esperimento presso la Torre degli Asinelli di Bologna. Qui scoprì il motivo per cui nessuno prima di lui era riuscito a portarlo a termine. Occorreva, in primo luogo effettuare calcoli che tenessero conto dell'attrito dell'aria, e, in secondo luogo, l'esperimento andava eseguito senza imprimere alle sfere il minimo spostamento laterale né la minima rotazione nel momento in cui esse erano lasciate cadere. Alcuni matematici partecipi alla sfida osservarono che la teoria elementare di Guglielmini non prendeva in considerazione vari fattori: la direzione della verticale mutava mentre la pietra cadeva, la deflessione aveva una componente diretta verso sud, le Alpi e la torre esercitavano forze gravitazionali, e così via. Guglielmini riuscì a risolvere il suo problema principale: per far cadere le sfere bruciò le corde che le sospendevano invece di tagliarle. Il risultato dell'esperimento, pubblicato nel 1792, poteva considerarsi in discreto accordo con la teoria. Altri grandi fisici matematici, fra cui Laplace e Gauss, migliorarono in seguito l'esperimento e la teoria su cui esso si fondava. La prima dimostrazione della deflessione verso est, che risultò immune da obiezioni, fu portata a termine alla Harvard University di Cambridge, circa un secolo dopo gli esperimenti di Guglielmini, dal professore americano Edwin Herbert Hall (1855-1938).

La gravitazione

La dottrina secondo la quale tutti i corpi gravitano, anche se può essere facilmente confermata dall'osservazione del comportamento della Luna e dei pianeti, non è facile da dimostrarsi per i corpi a portata di mano. Il problema si fece pressante intorno al 1770, quando i matematici iniziarono a supporre che le discrepanze nelle misurazioni degli archi di meridiano riscontrabili nelle rilevazioni geodetiche fossero causate dalla gravità. Il metodo abitualmente usato prevedeva che si determinasse la latitudine a ciascun estremo dell'arco, il che, a sua volta, dipendeva dall'uso di fili a piombo. I matematici ipotizzarono che il peso non desse indicazioni corrette a causa della deviazione dovuta alla distribuzione non omogenea delle masse gravitazionali nelle sue vicinanze. Verso la metà degli anni Settanta la Royal Society di Londra decise di verificare questa teoria, dietro insistenza dell'astronomo Nevil Maskelyne (1732-1811). Questi scelse una collina isolata in Scozia, abbastanza simmetrica perché si potesse stimarne la massa. Durante l'estate del 1774 i topografi effettuarono le misurazioni necessarie; tra l'altro, dedussero la distanza fra due stazioni, poste una a nord e una a sud della collina, la cui latitudine apparente era stata determinata dallo stesso Maskelyne con i metodi astronomici usuali. Chiamando A la differenza apparente della latitudine fra le due stazioni e T la differenza effettiva, ricavata dalla rilevazione, il doppio della deviazione del piombo dovuta all'effetto gravitazionale della collina, che chiameremo D, sarebbe stato perciò uguale ad A−T; poiché risultò che D equivaleva a circa sei secondi di arco (un dato che rientrava pienamente nell'ambito dell'accuratezza dei telescopi dell'epoca), l'esperimento confermò l'ipotesi che le montagne possono perturbare in modo significativo la misurazione della latitudine.

Questa ricerca produsse un altro risultato interessante. Charles Hutton (1737-1823), professore di matematica all'Accademia reale di Artiglieria di Woolwich e segretario della Royal Society, divise la collina in mille colonne cilindriche che riempivano il profilo individuato dalla rilevazione; da ciò, mediante calcoli elaborati, dedusse l'attrazione gravitazionale della collina e, avvalendosi della deviazione D misurata da Maskelyne, il rapporto della sua densità con quella della Terra. Supponendo che la collina avesse la densità della roccia normale, Hutton trovò che la densità della Terra doveva essere circa 4,5 volte quella dell'acqua, laddove Newton aveva stimato che questo valore fosse compreso tra 5 e 6.

Nel 1783 John Michell (1724-1793), prima professore di geologia a Cambridge e in seguito rettore di un'università di provincia, trovò un modo per 'pesare' la Terra senza allontanarsi da casa. Egli passò il decennio successivo a completare l'apparato necessario per effettuare la misurazione; sfortunatamente, non sopravvisse alla conclusione del suo lavoro. L'apparecchio passò a Henry Cavendish, che ultimò l'esperimento nel 1798; esso consisteva di una sottile asta che, sospesa orizzontalmente dalla sommità di un recipiente di vetro per mezzo di un filo, sosteneva una piccola sfera a ciascuna delle due estremità. Due grandi sfere di piombo potevano essere accostate a quelle piccole in modo da spostare lateralmente l'asticella sospesa di un angolo molto piccolo. La posizione di equilibrio forniva una relazione fra la lunghezza dell'asta, la costante di torsione, le masse piccole e grandi e la costante gravitazionale G. Cavendish allontanò le masse grandi e misurò la durata delle lentissime oscillazioni dell'asticella mentre riassumeva la posizione di riposo; il periodo di oscillazione dipende dal raggio della Terra, dalla densità di questa e dalla costante G. Cavendish, eliminando G (che compariva sia nelle equazioni dell'equilibrio sia in quelle dell'oscillazione), ottenne un valore per la densità in termini di grandezze misurabili. Tale valore si rivelò essere 5,48, compatibile con quello previsto da Newton e con quello attualmente considerato valido, ma non con quello calcolato da Hutton. Come Cavendish ebbe a dire nel dibattito che seguì la sua scoperta, il suo metodo aveva il vantaggio di fare a meno delle montagne.

La torsione

Il metodo di Michell richiedeva che la forza di torsione del filo di sospensione fosse proporzionale all'angolo di torsione. Secondo Cavendish, Michell sviluppò la sua bilancia di torsione prima d'imbattersi nella premiata memoria sulla torsione scritta nel 1780 da Coulomb, che era allora un esperto ingegnere militare, pronto a iniziare una brillante carriera all'Académie Royale des Sciences di Parigi. Coulomb cominciò a occuparsi della torsione per risolvere un vecchio problema di misurazione; la sua dimostrazione che le oscillazioni sotto torsione sono semplicemente armoniche gli permise in seguito d'introdurre misurazioni precise nell'ambito di settori del tutto nuovi della fisica.

Il vecchio problema di misurazione era quello del campo magnetico terrestre; i filosofi naturali avevano dimostrato ampiamente che tale campo subiva continue fluttuazioni giornaliere, e, in effetti, il principale antagonista di Coulomb nella competizione che lo portò a occuparsi di questo argomento, Jan Hendrik van Swinden (1746-1823), professore di filosofia all'Università di Franeker, presentò più di 40.000 osservazioni numeriche di questo fenomeno. Van Swinden effettuò le sue misurazioni avvalendosi dell'apparecchio che era allora usualmente impiegato nello studio del magnetismo, costituito da un ago magnetizzato imperniato su un sostegno appuntito e verticale. Tuttavia, le forze di attrito tendevano a sovrastare il piccolo valore della variazione diurna. Questo problema spinse l'Académie Royale des Sciences di Parigi a bandire una competizione, promettendo un premio a chi avesse trovato un perno più adatto o un metodo migliore di condurre l'esperimento. Coulomb ideò un metodo consistente nel sospendere l'ago con un sottile filo di seta, realizzando così quella che oggi chiamiamo 'bilancia di torsione'. Egli non soltanto dimostrò che la resistenza elastica alla torsione del filo era proporzionale all'angolo d'inclinazione dell'ago sul piano orizzontale, ma riuscì anche a ricavare la forza di torsione dalle dimensioni e dal materiale del filo. Nel 1780 l'Académie di Parigi rimpiazzò i suoi aghi montati su perni con lo strumento ideato da Coulomb. Il risultato fu però deludente, in quanto l'ago sospeso oscillava in maniera irregolare; Coulomb attribuì questo comportamento capriccioso all'elettricità statica accumulata sull'ago e sul suo contenitore. La soluzione più ovvia a tale inconveniente era quella di 'mettere a terra' il filo, il che imponeva di rimpiazzare il filo di seta con un filo metallico. Ciò costrinse Coulomb a intraprendere un lungo studio sulla torsione e sull'elasticità dei metalli da cui scaturì, nel 1784, un'opera fondamentale sulle leggi di coesione e di elasticità. Tra molte altre cose, Coulomb determinò la forza di torsione esercitata da un filo metallico ruotato di un angolo φ come −(μd⁴/e)φ, dove μ è una costante caratteristica del materiale del filo, d è il suo diametro ed e la sua lunghezza. Questa era la fisica francese che persino Thomas Young ammirava.

La capillarità

I filosofi illuministi erano affascinati dall'innalzamento e dall'abbassamento spontaneo dei liquidi contenuti in tubi sottili di vetro parzialmente immersi. Il motivo di questo interesse risiedeva nel fatto che si trattava di un fenomeno misurabile, poiché l'innalzamento o l'abbassamento dipendevano dal raggio del tubo e da altre grandezze geometriche. In quale modo potevano essere calcolate tali grandezze? L'approccio abituale si avvaleva della fisica della coesione, il che, per coloro che ragionavano al modo di Newton, implicava la considerazione delle forze a breve raggio fra le particelle del liquido e fra queste e le pareti del tubo. I primi calcoli approfonditi e convincenti furono portati a termine da Alexis-Claude Clairaut (1713-1765) nella sua opera Théorie de figure de la terre del 1743. Cinquant'anni dopo, Laplace portò a termine un'analisi simile, ma con un caratteristico cambiamento di prospettiva che fece della sua teoria un caso esemplare di fisica matematica.

Laplace suppose che il menisco liquido-aria avesse la forma di una superficie sferica; ciò gli consentiva di dedurre una relazione tra l'innalzamento h del liquido, il raggio r del tubo e l'angolo di contatto φ, con il seguente procedimento. La forza f che si esercita su una colonna infinitesimale del liquido EF equidistante dalle pareti e in contatto con la parte più bassa del menisco E è uguale all'integrale delle forze microscopiche che agiscono fra le particelle dell'acqua contenuta nel tubo e le particelle situate in E, e ha la forma: f=J+(1/b)K, dove J e K sono gli integrali delle forze microscopiche perpendicolari al canale esercitate sulle goccioline di E; poiché il contributo dei loro integrandi è nullo per distanze da E sensibilmente maggiori di zero, Laplace assegnò agli integrali i limiti zero e infinito, piuttosto che zero e il raggio d'azione della forza microscopica, e perciò i suoi calcoli non fornivano alcuna informazione sulle forze che si supponeva fossero in gioco.

Questo calcolo permise di raggiungere un traguardo importante. Se nella precedente equazione b è infinito, il menisco è piatto e non vi è forza di capillarità; perciò K/b può essere interpretato come la forza che sostiene la colonna capillare EF di peso δgh (dove δ rappresenta la densità dell'acqua e g l'accelerazione di gravità). Poiché 1/b=cosφ/r, allora h= Kcosφ/(rδg), ossia l'innalzamento per capillarità è inversamente proporzionale al raggio del tubo capillare e alla densità del fluido in esso contenuto. Il significato di J non era chiaro. Le misure ottenute da Haüy, che dedusse il raggio interno dei tubi capillari dal peso che avevano quando erano riempiti di mercurio, confermarono in pieno la teoria, introducendo così, secondo le parole di Laplace, "la precisione delle misurazioni astronomiche" nella fisica.

Il circolo di Laplace celebrò la sua trattazione dell'innalzamento per capillarità come un capolavoro della teoria fisica; secondo Haüy, esso unificava il mondo materiale. Laplace, infatti, usava le stesse formule per spiegare la capillarità e per "spiegare i maggiori fenomeni dell'Universo". Inoltre, aggiunse Biot, avendo individuato con precisione "la vera causa" dell'innalzamento dei fluidi nei tubi sottili, Laplace era sul punto di arricchire la chimica di un'appropriata teoria dell'affinità. Soltanto una vera mente superiore avrebbe potuto dominare gli aspetti più rilevanti della matematica, dell'astronomia, della fisica e anche della chimica. Ancora nelle parole di Haüy: "è a tale superiorità […] che dobbiamo questa splendida teoria dei fenomeni che si verificano nei tubi capillari" (Traité élémentaire de physique, ed. 1806, I, p. 213).

Le proteste dei critici non si fecero attendere. Young liquidò la teoria di Laplace come inutilmente complicata e priva di qualsiasi novità. John Playfair (1748-1819), professore di filosofia naturale all'Università di Edimburgo, contestò invece a Laplace di aver invertito causa ed effetto, poiché a provocare l'innalzamento non sarebbe la concavità del menisco ma piuttosto l'attrazione fra il liquido e il vetro. Gauss, nel 1829, giudicò che l'analisi non era "conforme alla fondazione matematica esatta delle altre teorie [di Laplace], ma sembrava presentare piuttosto le intuizioni vaghe che in precedenza i fisici avevano avuto a proposito dell'intero fenomeno" (Briefwechsel zwischen Gauss und Bessel, p. 489).

Ciononostante, la trattazione della capillarità effettuata da Laplace continuò ad avere un ruolo dominante per tutto il XIX sec., in parte a causa del fatto che K è strettamente connesso alla costante della tensione superficiale. Il fenomeno rappresentato da J avviene nei gas oltre che nei liquidi. Johannes Diderik van der Waals (1837-1923) riprodusse e approfondì nella sua famosa tesi del 1873 la derivazione di J e K effettuata da Laplace; in questo lavoro egli modificò la legge dei gas perfetti per tenere conto di J e cancellò la distinzione fra liquidi e gas. Dunque, la totale matematizzazione delle forze a distanza portò alla fine a fondamentali scoperte fisiche.

5. La 'physica particularis'

L'ambiguo concetto di forza

La crescita più rapida della fisica quantitativa intorno al 1800 avvenne nei settori definiti dagli imponderabili. I primi risultati esemplari furono gli esperimenti classici, anche se irripetibili, effettuati da Coulomb negli anni Ottanta del Settecento con la bilancia di torsione. Essi stimolarono un rapido processo di espansione e affinamento della teoria elettrostatica, che avvicinò la vaga nozione di 'tensione' al moderno concetto di 'potenziale'. La teoria del magnetismo seguì un percorso analogo, anche se i contributi decisivi vennero dall'esterno della Francia. La teoria del calorico divenne il terreno di esercitazione proprio degli allievi di Laplace, un gruppo formato principalmente da laureati dell'école Polytechnique; tale gruppo si riunì intorno al maestro dopo che l'Académie Royale des Sciences di Parigi, che era stata soppressa nel 1794, rinacque come Prima classe dell'Institut de France, inaugurato nel 1795. Questo gruppo godeva dell'appoggio di Laplace, che era a sua volta protetto da Napoleone, e includeva, per menzionare soltanto gli scienziati le cui opere verranno trattate in questa sede, Biot, Joseph-Louis Gay-Lussac (1778-1850), étienne-Louis Malus (1775-1812), Alexis-Thérèse Petit (1791-1820) e Pierre-Louis Dulong (1785-1838).

I filosofi della Natura quantitativi, nel tentativo d'inferire la legge della forza operante fra le particelle microscopiche dei loro fluidi senza peso, si trovavano di fronte a un duplice insieme di difficoltà. In primo luogo, occorreva costruire uno strumento che fornisse una misura affidabile, necessariamente macroscopica, di un effetto che si supponeva fosse causato dal fluido imponderabile; in secondo luogo, si doveva dedurre la legge dalla misurazione. In pratica, questa sequenza fu spesso invertita, come avvenne nelle deduzioni della legge della forza elettrica da parte di Cavendish e di Coulomb. Questa tecnica diede i risultati sperati nel caso dell'elettricità e del magnetismo; invece, gli sforzi per ricavare la forza di repulsione del calorico, o le forze che agiscono fra i raggi luminosi e la materia o, nel caso della coesione e dell'adesione, fra materia e materia furono fallimentari. In pratica, Laplace, mediante la stessa tecnica che aveva usato per aggirare la conoscenza della forza capillare, sembrò fondare la sua analisi quantitativa del calore e della luce sulle forze microscopiche, senza determinare in quale misura tali forze dipendessero dalla distanza. In casi come questi Laplace e la sua scuola ottennero relazioni matematiche fra quantità macroscopiche senza scoprire nessuna caratteristica quantitativa dei fluidi in sé.

è difficile tenere a mente la distinzione fra le misurazioni dirette delle forze ponderomotrici macroscopiche e le inferenze riguardanti le forze microscopiche esercitate da particelle di materia o da fluidi privi di peso. I primi sforzi per giungere alle leggi della forza naufragarono per via di una confusione circa questi due significati. Al fine di evitare circonlocuzioni e di chiarire la situazione dei protagonisti della vicenda storica, è utile distinguere i vari significati del termine forza. Indicheremo qui con il termine forza, in caratteri corsivi, un'attrazione o una repulsione elementare e microscopica fra gli elementi dei fluidi, fra di essi e le particelle di materia e fra le particelle di materia; con il termine forza, in caratteri tondi, indicheremo invece una causa ponderomotrice misurabile, ossia quell'agente che, secondo le leggi di Newton, è responsabile dei movimenti o degli equilibri osservabili; indicheremo poi con il termine 'forza' tra apici un qualcosa di generico e indistinto fra forza e forza.

Il magnetismo

I discepoli diretti di Newton tentarono d'individuare la 'forza' dei magneti prima ancora che il concetto di materia imponderabile fosse stato perfezionato. Essi scelsero come oggetto dei loro esperimenti un blocco di magnetite ‒ roccia che si presenta magnetizzata naturalmente ‒ e cercarono di trovare, in analogia con la teoria della gravitazione, la legge secondo la quale la 'forza' che il blocco esercitava sull'ago di una bussola diminuiva all'aumentare della distanza. Questi esperimenti non produssero risultati coerenti o generali, poiché la legge dipendeva dalle circostanze particolari di ciascun assetto sperimentale, quali la forma della magnetite, la definizione dei suoi poli magnetici, le distanze implicate. Gli esecutori delle misurazioni non avevano seguito fino in fondo l'analogia con la teoria gravitazionale; infatti, non avevano supposto che la sostanza o le sostanze magnetiche fossero formate da particelle, ciascuna delle quali agiva sulle altre tramite la stessa forza elementare, ossia che la forza osservata sul modello fosse la somma di tutte le forze esercitate fra tutte le coppie di particelle.

Coulomb prese sul serio la necessità di calcolare la forza del magnetismo come l'integrale delle forze, e il suo tentativo fu coronato da successo; egli comprese che il modo concreto per portare a termine l'integrazione era l'uso di una geometria il più possibile vicina a quella che rendeva il mondo un sistema calcolabile. Invece di impiegare magnetiti di forma irregolare, egli usò magneti artificiali d'acciaio della lunghezza di 65 cm, con poli definiti chiaramente, situati a 2,25 cm da ciascuna estremità; in tal modo poté supporre che i fluidi magnetici di ciascun magnete fossero coagulati in due punti distinti e distanti fra loro. Coulomb sospese orizzontalmente sul meridiano magnetico un magnete lungo e sottile (fig. 6, la freccia orizzontale posta al disotto dell'asse della bilancia), servendosi di un filo attaccato al suo baricentro; inoltre, dispose verticalmente un secondo magnete, simile al primo, con il Polo Nord opposto a quello del magnete sospeso (nella fig. 6, la barretta verticale a destra rispetto all'asse della bilancia). La forza repulsiva causata da tutte le forze esercitate fra le particelle della materia boreale (ossia del Polo Nord) provocava la rotazione del magnete sospeso.

Il calcolo dipendeva dalla misurazione dell'angolo di torsione del filo nel momento in cui il magnete sospeso raggiungeva lo stato di equilibrio, condizione, quest'ultima, difficile da identificare nella pratica. Si chiami ω l'angolo di torsione e φ l'angolo compreso fra il piano del magnete sospeso e il suo meridiano magnetico. Coulomb misurò tre coppie di valori per ω e φ. Egli sapeva che la torsione esercitata dal campo magnetico terrestre sul magnete era proporzionale all'angolo di spostamento φ, ossia valeva bφ, con b costante, e partiva dal presupposto che la forza elementare diminuisce in ragione del quadrato della distanza e che la geometria permette l'approssimazione per la quale tutte le particelle del fluido in un polo agiscono come se fossero concentrate in un punto. Per questo si aspettava di trovare a/φ²=bφ+ω, dove a e b sono due costanti dell'esperimento. Le sue misurazioni indicavano che i tre valori di φ² stavano approssimativamente tra loro come 4, 2 e 1, mentre quelli di (bφ+ω) stavano tra loro come 1, 2 e 4, "per cui [poiché a risultava essere una costante, come richiesto] l'azione repulsiva del fluido magnetico è inversamente proporzionale al quadrato delle distanze" (Deuxième mémoire sur l'électricité et le magnétisme, 1785, p. 578).

Coulomb non poteva misurare l'attrazione corrispondente fra poli differenti con la sua bilancia di torsione, poiché la loro attrazione non permetteva un equilibrio stabile, eccettuato il caso in cui essi si toccavano. Egli escogitò la soluzione ingegnosa di misurare il periodo delle oscillazioni di un ago magnetizzato che era sospeso a varie distanze dal polo di un magnete fisso. Questa analisi richiedeva di assumere la legge della forza e di controllare che la frequenza delle oscillazioni diminuisse adeguatamente in ragione della distanza. Coulomb effettuò un insieme di misurazioni per ciascuna delle tre distanze differenti che egli aveva stabilito; i risultati che riportò si accordavano alla teoria con uno scarto contenuto entro il 15%.

Coulomb aveva misurato la forza fra poli molto distanti. Per dedurre la forza operante fra gli elementi dei fluidi, la concentrazione dei quali doveva, secondo le sue supposizioni, formare i poli, egli usò il teorema dimostrato da Newton nel caso della gravità, secondo cui una sfera uniforme di particelle ciascuna delle quali attragga o respinga una particella simile situata al di fuori della sfera agisce come se tutta la materia di cui essa è formata fosse collocata al suo centro. Molte altre misurazioni confermarono il ragionamento di Coulomb e i risultati che egli aveva ottenuto. Questa ricerca, oltre a determinare il carattere dei fluidi magnetici, ebbe delle applicazioni assai più vaste. Le misurazioni più elaborate su quest'argomento furono effettuate da Christopher Hansteen (1784-1873), che calcolò l'orientamento degli aghi delle bussole nell'ipotesi che la Terra dovesse il suo magnetismo a due magneti di dimensioni e intensità diverse. Le misure e i calcoli sofisticati di Hansteen, incoraggiati da un premio che l'Accademia delle Scienze danese bandì nel 1811, furono pubblicati nel 1819, tre anni dopo la sua nomina a professore di matematica applicata e astronomia all'Università di Christiania (attuale Oslo).

L'elettricità

Lo studio della forza elettrica seguì lo stesso corso dello studio di quella magnetica. All'inizio, il fallimento del tentativo di trovare una stretta analogia con la teoria gravitazionale diede luogo a numerose 'leggi di forza', differenti fra loro e applicabili esclusivamente alle particolari circostanze sperimentali in cui erano state ricavate. I primi tentativi basati sulla geometria newtoniana furono compiuti da uno scozzese e da un inglese, ma nessuno dei due diede alle stampe i risultati del proprio lavoro. John Robison (1739-1805), che aveva studiato filosofia naturale con Joseph Black a Glasgow, fu il primo di questi due misuratori. Egli affrontò i problemi legati alla forza elettrica intorno al 1770, mentre era segretario di una missione navale inglese in Russia. Senza dubbio il suo lavoro fu stimolato dal fatto di aver conosciuto gli studiosi di San Pietroburgo, in particolare Aepinus, che aveva elaborato una teoria dell'elettricità basata rigorosamente sul concetto newtoniano di forza come somma di forze. Egli aveva ipotizzato, senza tuttavia dimostrarlo, che la legge della forza valida per l'elettricità diminuisse in ragione inversa del quadrato della distanza fra gli elementi interagenti.

Robison fissò a un asse elettricamente isolante un filo di seta cerata che reggeva una sfera di sughero ricoperta d'oro, in modo tale che esso potesse ruotare liberamente su un piano verticale; all'inizio della misurazione la sfera di sughero poggiava su un'altra sfera fissa isolata di ottone. Robison elettrizzò la coppia di sfere in modo che la conseguente repulsione reciproca facesse ruotare la sfera di sughero di un angolo α, dalla misura del quale egli poté dedurre il peso che la forza elettrica poteva sostenere contro la gravità. Robison costruì le due sfere con un diametro piccolo rispetto alla distanza che le separava; ciò gli consentì di effettuare i calcoli come se le intere cariche fossero situate nel centro delle sfere, e quindi lo mise in grado di dedurre la legge della forza dalla misurazione di α e dalle dimensioni dell'apparato. Egli affermò in seguito di aver effettuato "molte centinaia" di misure e di aver ricavato da esse l'informazione che la forza dell'elettricità diminuisce in ragione della distanza elevata a 2,06.

Il secondo misuratore fu Cavendish; nel 1771 egli pubblicò un articolo lungo e complesso, nel quale dedusse le proprietà di un fluido le cui parti interagiscono a distanza secondo una forza che diminuisce in ragione di una potenza della distanza pari a n. Secondo un teorema di Newton, una massa all'interno di un guscio sferico omogeneo non è soggetta ad alcuna forza gravitazionale netta. Generalizzando tale teorema si otteneva che, nel caso in cui n=2, tutto il fluido elettrico presente su un conduttore sferico carico avrebbe dovuto disporsi sulla sua superficie. Cavendish mostrò poi, con un esperimento magistrale, che la carica comunicata all'interno di un guscio conduttore fluiva immediatamente verso l'esterno; invertendo il ragionamento, concluse che n=2, o meglio che n non poteva differire da 2 di più di 1/50. Questa stima, forse la prima nel suo genere, conseguiva dall'ipotesi che l'interno della sfera potesse trattenere una carica appena inferiore al valore minimo che Cavendish era in grado di rilevare.

Coulomb non era soggetto alla riservatezza britannica e aveva anzi l'obbligo accademico di pubblicare. Il suo apparato è ormai ben noto. All'estremità inferiore di un filo di seta cerato, fissato superiormente a una manopola, era sospesa un'asticella orizzontale ai cui estremi vi erano, rispettivamente, la sfera soggetta all'azione elettrostatica e un dischetto di carta, che doveva servire a ridurre le oscillazioni. Coulomb elettrizzò una sfera di ottone fissa e la pose in contatto con quella mobile, che si allontanava oscillando dall'altra a causa della repulsione reciproca. Egli osservò che, per via della dimensione ridotta della sfere (1 cm di diametro) rispetto alla loro distanza reciproca, poteva ragionare come se le cariche fossero concentrate al centro di esse. Per ciò che riguarda la misurazione stessa, egli la portò a termine nello stesso modo in cui aveva condotto il corrispondente lavoro sul magnetismo. Questa volta l'equilibrio richiedeva che φω² fosse una costante. Come aveva fatto in precedenza, Coulomb assegnò a ω e φ soltanto tre coppie di valori, che diedero tre valori per φω², due dei quali identici; il terzo valore poteva essere uguagliato agli altri due assumendo un errore di 9° nella misura del terzo valore di φ. "Ne segue", scrisse Coulomb, "che la mutua azione di repulsione che ha luogo fra due sfere cariche di elettricità della stessa specie è inversamente proporzionale al quadrato delle distanze" (Deuxième mémoire sur l'électricité et le magnetisme, p. 569).

Per misurare l'attrazione e inferire la forza fra cariche di segno opposto, Coulomb si servì delle oscillazioni, come aveva già fatto nel caso analogo del magnetismo. Ancora una volta effettuò solamente tre misurazioni per confermare l'ipotesi di una forza inversamente proporzionale al quadrato della distanza, ipotesi che egli doveva assumere per calcolare la dipendenza del periodo delle oscillazioni dalla distanza fra le cariche interagenti. La misurazione si accordò con la teoria quasi altrettanto bene di quanto era avvenuto nel caso del magnetismo, ossia con un errore del 15% circa.

La parsimonia di Coulomb nell'uso dei numeri e il consenso che i suoi colleghi accademici tributarono alle importantissime conclusioni che egli trasse da essi indicano che, agli albori della fisica matematica, una teoria matematica poteva essere confermata da pochi valori significativi, piuttosto che da tabelle piene di dati, ossia che pochi valori significativi erano sufficienti se la teoria era considerata plausibile e le sue conseguenze accettate in anticipo; se però il programma di Newton fosse stato ancora in dubbio, né i calcoli di Coulomb né le sue conclusioni avrebbero potuto imporre il consenso che ricevettero. Non soltanto molte misure deviavano in maniera rilevante dalle aspettative, mentre altre corrispondevano in maniera sospetta ai calcoli, ma anche l'apparato funzionava male, dato che la posizione di zero della bilancia di torsione si spostava durante gli esperimenti.

Alcuni elettrologi più anziani di Coulomb, come Jean-André Deluc (1727-1817) e Alessandro Volta, i quali non credevano che la soluzione della teoria elettrica potesse provenire dal concetto newtoniano di forza, ritenevano che le conclusioni di Coulomb valessero soltanto per il particolare dispositivo sperimentale che egli aveva utilizzato. Gli elettrologi tedeschi non apprezzavano le sue conclusioni o addirittura le rifiutavano. Paul Ludwig Simon (1767-1815) di Berlino e Georg Friedrich Parrot (1767-1852) di Dorpat, che non erano assolutamente contrari a trattare l'elettricità secondo lo schema newtoniano, respinsero le conclusioni di Coulomb poiché non furono in grado di ottenere misure coerenti con un apparato così instabile.

La bilancia di Coulomb non permette di effettuare misurazioni esatte e coerenti; lo spostamento della posizione di zero non può essere compensato se non mediante approfondite ricerche ausiliarie. è molto difficile mantenere il movimento dell'ago sul piano prefissato, e inoltre il filo sottoposto a torsione è soggetto alla cosiddetta 'isteresi elastica', un fenomeno, questo, scoperto negli anni Trenta dell'Ottocento nel corso di una serie di esperimenti volta a chiarire le ambiguità e le disomogeneità delle misurazioni effettuate con la bilancia di torsione. La legge di Coulomb fu accettata più per il potere dell'analogia che per il valore effettivo delle misure. Le intensità di elettricità e magnetismo, come quella della gravità, diminuiscono a distanze macroscopiche, e tuttavia rimangono sensibili. Perché non dovrebbero seguire tutte la legge del quadrato della distanza?

Gli elettrologi, in qualsiasi modo considerassero la forza di Coulomb, sapevano che essa non sarebbe stata di grande aiuto per comprendere le misurazioni della 'tensione elettrica', della 'quantità di elettricità' e della 'capacità elettrica' che essi effettuavano ordinariamente. Coulomb aveva connesso queste quantità macroscopiche al suo modello microscopico tramite il concetto di 'densità del fluido elettrico'; un concetto del genere era necessario poiché si sapeva che il fluido elettrico, al contrario del fluido bloccato all'interno dei poli magnetici, si muove nei conduttori. Per essere certi che la forza elettrica si annulla all'interno di un conduttore, il fluido deve in generale distribuirsi sulla superficie in maniera non uniforme, vale a dire con densità diseguale. Allo scopo di individuare punto per punto le densità relative, Coulomb aveva inventato il 'piano di prova', un sottile disco di carta dorata attaccato a un'impugnatura isolante: quando il piano di prova era messo in contatto con un conduttore elettrizzato, riceveva una carica proporzionale alla densità del fluido elettrico nel punto di contatto. Coulomb assegnò un numero alla densità relativa nel punto di contatto, osservando l'oscillazione del braccio della sua bilancia di torsione, dopo che essa era stata elettrizzata mettendo in contatto il piano caricato con il pomo della bilancia. Questa tecnica gli permise di confermare i calcoli sulla distribuzione del fluido elettrico nei conduttori sferici carichi posti a contatto tra loro. Le misure si accordavano approssimativamente con i calcoli, e ciò costituì un determinante appoggio indiretto alla legge del quadrato della distanza, sulla quale tali calcoli erano fondati.

Il rudimentale elettroscopio a filo determinò lo sviluppo di un approccio più approfondito alla misurazione della 'quantità' di elettricità. Tale strumento aveva raggiunto nei primi anni Settanta la forma tipica illustrata nell'opera di William Henley (m. 1779), protetto di Joseph Priestley (1733-1804); esso indicava la carica con l'angolo formato dall'indice e dall'asticella, nel momento in cui l'apparecchio poggiava su un conduttore carico. Altre versioni migliorate dei fili divergenti si rivelarono utili in altre situazioni: nell'elettroscopio a foglie d'oro di Abraham Bennet (1750-1799) del 1786, la carica trasmessa al coperchio dello strumento faceva divaricare le foglie di un angolo che misurava in qualche modo l'elettricità del corpo che forniva la carica.

Che cosa misurava in effetti l'angolo di divaricazione (che chiamiamo α)? Negli anni Ottanta, Volta si avvicinò molto alla risposta a questa domanda; egli sapeva che α non indicava esattamente la quantità di carica Q di un conduttore isolato in contatto con l'elettroscopio, infatti, come aveva brillantemente dimostrato nel 1778, l'ampiezza di α non dipende solamente da Q, ma anche dalla forma del conduttore. La dimostrazione che egli diede è la seguente. Una serie di cilindri di metallo, sospesi da fili isolanti, contengono una quantità maggiore di fluido elettrico (misurato dalle rotazioni della macchina elettrica o dalla scossa che trasmettono) quando sono appesi a una certa distanza l'uno dall'altro rispetto a quando sono posti l'uno vicino all'altro. Non soltanto la forma geometrica del conduttore, ma anche la presenza di altri corpi conduttori nelle sue vicinanze influiscono su quella che Volta aveva denominato la "capacità elettrica" del conduttore stesso. Perciò α, più che misurare la quantità di fluido, indicava qualcosa di più difficile da visualizzare: la sua pressione, o, come Volta preferiva chiamarla, la sua "tensione" (Cavendish aveva richiamato l'attenzione su questa distinzione in un complesso articolo del 1771). Volta ipotizzò che la quantità Q di fluido dipendesse in maniera lineare dalla tensione T, misurata da α, e che la capacità C fosse espressa dal loro rapporto: Q=CT, ossia C=Q/T.

Per dimostrare questa seconda relazione, Volta calibrò una coppia di pagliuzze metalliche, che dovevano assolvere la stessa funzione delle foglie d'oro dell'elettrometro di Bennet, in modo che registrassero incrementi uguali di α in corrispondenza d'incrementi uguali della carica. Egli trasmise al pomello dell'elettrometro una quantità di fluido Q tale da separare le pagliuzze per un angolo massimo di ampiezza β; mise poi in contatto il pomello con quello di un altro elettrometro identico al precedente, riducendo di conseguenza la carica a Q/2 e l'ampiezza dell'angolo a un valore che egli chiamò β/2, e così via. Volta utilizzò il suo strumento a pagliuzze calibrato in questo modo per ottenere i valori di Q/C di molti conduttori in diverse circostanze e per conoscere, nel caso di conduttori che si muovono sotto l'influenza di altri conduttori, quanto varia la capacità di uno di essi se è separato dagli altri. Egli sfruttò l'esperienza che aveva accumulato lavorando con l'elettrometro a pagliuzze e individuando cariche ridotte nella competizione con Luigi Galvani (1737-1798) che portò all'invenzione della pila.

Il calore

L'analogia qualitativa fra il calorico e il fluido elettrico (o i fluidi elettrici) riguardo alla latenza e alla tendenza a espandersi, e quella fra la relazione di entrambi con la materia ordinaria riguardo alla capacità, si articolò ulteriormente sotto l'impulso della misurazione. Come nel caso dell'elettricità, gli strumenti per misurare il calorico erano essi stessi influenzati dai procedimenti di misurazione. Proprio come nella bilancia di Coulomb l'elettricità studiata induceva cariche sull'apparato e sullo stesso sperimentatore che a sua volta esercitava forze sulla bilancia, così parte del calore comunicato al termometro era consumata nella dilatazione dello strumento che effettuava la misurazione. Inoltre, in entrambi i casi, l'affidabilità o la linearità degli strumenti diedero luogo a dispute ricorrenti e produttive.

A buona ragione si può fissare come punto d'inizio della moderna termometria il lavoro della commissione che nel 1776 fu nominata dalla Royal Society per scoprire il motivo per cui i termometri della società stessa non davano mai risultati concordanti; la composizione di tale commissione, che comprendeva Maskelyne e un altro astronomo, un medico, il meteorologo Deluc e aveva come presidente Cavendish, che rappresentava la fisica e la chimica, indicava con quale ampiezza il problema della misurazione del calore fosse avvertito nella scienza dell'epoca. La commissione cercò d'individuare il punto di ebollizione di molti termometri a mercurio e trovò discrepanze di oltre 3 °C. Gli scienziati attribuirono queste variazioni a differenze operative (gli operatori collocavano i bulbi in luoghi differenti durante la taratura) e alle differenze della pressione atmosferica; essi raccomandarono un protocollo uniforme per determinare il punto di ebollizione e per compensare le piccole irregolarità nella graduazione fra i punti fissi.

La termometria a gas, come la costruzione delle macchine a vapore, richiedeva che fosse determinato il coefficiente di dilatazione termica dei gas, ε. Le peculiarità costruttive di ciascun termometro e la difficoltà di asciugarlo completamente, nonché la differenza delle tecniche sperimentali utilizzate, davano luogo a un gran quantità di valori discordanti; subito dopo la fine del secolo, stimoli sia teorici sia pratici finirono per generare un maggiore consenso. Dal punto di vista teorico, John Dalton (1766-1844) e altri scienziati, per i quali un gas non era altro che un insieme di particelle prive d'interazione reciproca e che nuotavano in un mare di fluido calorico, supposero che tutti i gas dovessero mostrare il medesimo comportamento meccanico in seguito all'azione del calorico. Dalton imputò alla presenza di vapori o ad altre impurità le discrepanze che si manifestavano nelle misure dei coefficienti di espansione dei gas. Egli stesso non effettuò le misurazioni con cura sufficiente da rendere del tutto persuasiva la sua asserzione, secondo la quale tutti i fluidi elastici, a parità di pressione, subiscono la stessa espansione termica.

Gay-Lussac s'impegnò a fondo per assegnare al coefficiente ε un valore corretto, per l'importanza che aveva nell'astronomia (nel calcolo della rifrazione atmosferica), nella tecnologia (per le macchine termiche), nella fisica e nella chimica (per i volumi dei gas), nella meteorologia (per l'evaporazione e l'umidità atmosferica) e nell'ipsometria (per determinare le altitudini mediante il barometro). Il metodo che lo portò al successo era il seguente. Egli riempì di gas una fiala di vetro, la scaldò mentre era chiusa e aprì una valvola, in modo che il gas dilatato potesse raggiungere una situazione di equilibrio con l'atmosfera; in seguito chiuse la valvola, raffreddò la fiala e riaprì la valvola sott'acqua; la quantità di acqua spinta nella fiala dalla pressione atmosferica indicava la quantità di gas espulso quando la temperatura era più elevata, e quindi il coefficiente di espansione a pressione costante. Gay-Lussac riteneva che il risultato che aveva ottenuto (ε=1/267 per grado centigrado) fosse valido per tutti i gas e per tutte le temperature comprese fra quella di congelamento e quella di ebollizione.

Il coefficiente ε di Gay-Lussac era sia un risultato sia una premessa della sua misurazione, basata sul presupposto che incrementi uguali di temperatura registrati da un termometro a mercurio sono proporzionali ad aumenti uguali del volume del gas che si espande. Se indichiamo con θ la lettura del termometro e con V il volume corrispondente del gas, è V₂−V₁=V₀ε(θ₂−θ₁), dove V₀ indica il volume alla temperatura di riferimento, diciamo a 0 °C; questa equazione può essere riscritta nel modo seguente: V=V₀(1+εθ). Poiché, secondo la legge di Boyle, pV=n×costante, dove n misura la quantità di gas nel campione, l'equazione pV=nT×costante, dove T=θ+(1/ε), dovrebbe descrivere il comportamento di un gas in generale. Quest'ultima equazione è conosciuta come 'legge di Gay-Lussac' o 'di Charles', dal nome del fisico Jacques-Alexandre-César Charles (1746-1823), al quale Gay-Lussac riconobbe il merito di aver indicato per primo, in una serie di esperimenti non pubblicati, che tutti i gas si espandono allo stesso modo quando sono riscaldati.

La legge di Charles e Gay-Lussac liberò la termometria dalla dipendenza dallo strumento in base al quale era stata scoperta, il termometro a mercurio, e da altri materiali di tipo particolare. Come l'introduzione di una geometria coerente con la teoria newtoniana dei fluidi imponderabili aveva dato modo agli sperimentatori di dedurre proprietà della forza che fossero applicabili a tutti i fenomeni magnetici o elettrici, e non esclusivamente all'apparato particolare usato in questa o quella ricerca, così la scoperta della regolarità del termometro a gas secco offriva uno strumento universale di misurazione del calore e della temperatura.

Gli studiosi di termometria, dopo aver accettato i risultati di Dalton e Gay-Lussac, invertirono il loro approccio e calibrarono i termometri a mercurio e di altro tipo in modo che si accordassero con i termometri ad aria. Per sfuggire al circolo vizioso, questi ultimi erano calibrati per segnare uguali incrementi di volume sulla loro colonna, con un procedimento in qualche modo analogo a quello seguito da Volta per calibrare l'elettrometro a pagliuzze. Le misure meticolose di Dulong e Petit, pubblicate nel 1818, mostravano che fra 0 e 100 °C il termometro a mercurio e quello a gas si muovevano parallelamente, mentre per temperature maggiori il primo cresceva più rapidamente: quando la colonnina di quest'ultimo indicava 300 °C, il termometro ad aria segnava appena 292 °C.

Tav. I

Come è ben noto ai matematici, quantità immaginarie possono dar luogo a misure reali; un esempio elegante di questa circostanza è dato dalla calorimetria di Lavoisier e Laplace. Essi inventarono uno strumento, il calorimetro a ghiaccio (per la descrizione v. Tav. I), che aveva il notevole vantaggio, come dissero i due scienziati, di poter produrre valori relativi alla quantità di calore "indipendenti da qualsiasi ipotesi riguardo alla [sua] natura"; essi affermarono che lo scopo primario che li animava nel comunicare i loro dati era di presentare lo strumento e di raccomandarlo per la sua "precisione e generalità", senza pronunciarsi sulle verità della termodinamica, e ciò era vero anche se essi avevano una predilezione per la teoria della materia.

Lavoisier e Laplace si aspettavano che il loro metodo avrebbe soppiantato l'adattamento al calcolo dei calori specifici dei metodi precedenti, usati per determinare la temperatura di una miscela di acqua calda e fredda. In questo tipo di adattamento, impiegato nella pratica da Wilcke e Black, il misuratore immergeva un oggetto riscaldato a una temperatura T₁ in un'uguale massa d'acqua a temperatura T₂; se η è la temperatura di equilibrio e c il calore specifico dell'oggetto, è c=(η−T₂)/(T₁−η). Lavoisier e Laplace osservarono che questa tecnica era assai imprecisa per sostanze che avessero un calore specifico molto differente da quello dell'acqua e per quelle misurazioni che richiedevano molto tempo per giungere allo stato di equilibrio; inoltre, era poco applicabile nel caso di sostanze che reagivano chimicamente con l'acqua o con il calore sviluppato dalla combustione o dalla respirazione. Con la loro descrizione del calorimetro a ghiaccio e la loro capacità di fornire dati sui calori specifici con sei cifre significative, Lavoisier e Laplace trasmisero ai filosofi naturali l'obiettivo, se non i mezzi, di realizzare misure di precisione sui fenomeni termici. Il calorimetro a ghiaccio ebbe perciò un ruolo analogo a quello della bilancia di torsione; coloro che accettavano il sistema degli imponderabili lo considerarono adeguato dal punto di vista teorico, ma in pratica poco preciso, e quindi finirono per usare molto poco entrambi gli strumenti. La fiducia incondizionata nel loro calorimetro spinse Laplace e Lavoisier ad adattarlo al difficile compito di misurare i calori specifici dei gas. Essi fecero in modo di produrre un flusso continuo di gas attraverso l'apparato e calcolarono la capacità termica specifica misurando la temperatura del gas all'entrata e all'uscita, la velocità di flusso e la quantità di ghiaccio che si scioglieva. Negli esperimenti portati a termine durante l'inverno fra il 1783 e il 1784, ma che non furono pubblicati prima del 1805, Laplace e Lavoisier assegnarono all'ossigeno un calore specifico pari a 0,65 e all'aria un calore specifico di 0,33031(!), ossia un valore uguale a quello di una quantità di acqua di uguale peso.

Gli scienziati che in seguito si dedicarono allo studio del calore specifico condivisero il pregiudizio, sostenuto da misuratori sciatti come Dalton o scrupolosi come Dulong e Petit, secondo il quale il mondo degli imponderabili era retto da leggi semplici. Dalton ideò numerose relazioni semplici, fra il volume e la temperatura di un gas e la distanza fra le sue particelle, e ipotizzò che ogni atomo di gas alla stessa temperatura avesse la stessa capacità per il calore. Dulong e Petit furono più fortunati nelle loro generalizzazioni. Essi supposero che il calore specifico di ogni atomo di metallo, c_a, fosse una costante e quindi effettuarono le loro misurazioni. Portando i loro campioni di metallo a una temperatura leggermente maggiore di quella dell'aria, essi misurarono il tempo t che ciascun campione impiegava per tornare alla temperatura ambiente; assumendo che il calore specifico c per unità di peso fosse proporzionale a t, essi ottennero per i calori specifici valori con tre cifre significative. Ora c_a=c/n, dove n rappresenta il numero di atomi presenti in un'unità di peso della sostanza che si prende in considerazione; e n=costante/A, dove A è il peso atomico della sostanza. Le misurazioni effettuate su tredici metalli, nelle loro unità, assegnarono a cA valori da 0,3685 a 0,3830, che comportavano che c_a fosse costante. "Un semplice esame di questi numeri mette in luce una vicinanza che è troppo notevole nella sua semplicità per non suggerire immediatamente l'esistenza di una legge fisica passibile di essere generalizzata ed estesa a tutte le sostanze naturali" (Sur quelques points importants de la théorie de la chaleur, 1819, pp. 398-405). Anche Dulong e Petit avevano però tirato troppa acqua al loro mulino, nonostante la loro legge sia vera con una buona approssimazione nel caso dei metalli a temperatura ambiente.

Le prime misurazioni affidabili dei calori specifici dei gas furono effettuate nel contesto di una competizione organizzata dalla Classe Prima dell'Institut de France. Due coppie di ricercatori risposero all'appello: François Delaroche e Jacques-Étienne Bérard, due medici lontanamente legati al circolo di Laplace, che vinsero il premio, e Nicolas Clément e Charles-Bernard Desormes, entrambi chimici industriali, che ottennero una menzione d'onore. Scopo secondario della competizione (il primo era quello di misurare il calore specifico) era di colpire la setta scismatica che si era formata fra i seguaci del calorico, rappresentata nel 1812 da Dalton e John Leslie, professore di matematica e filosofia naturale all'Università di Edimburgo, che aveva negato l'esistenza del calore latente o legato. Secondo il loro punto di vista, il calore sviluppato in un qualsiasi processo sorgeva a causa di alterazioni nel calore specifico dei corpi che erano soggetti al mutamento; di conseguenza, essi attribuivano al vuoto un calore specifico finito. Delaroche e Bérard aderivano alla posizione ortodossa della scuola di Lavoisier; Clément e Desormes mostrarono invece di essere stati contagiati dall'eresia di Dalton. Comunque, entrambe le coppie di studiosi ottennero valori eccellenti per i calori specifici dei gas più comuni.

La velocità del suono

Quattro generazioni di filosofi naturali avevano tentato, senza successo, di cancellare la divergenza fra il valore teorico della velocità del suono calcolato da Newton, ossia 1000 piedi al secondo (305 m/s), e il risultato sperimentale di 1142 piedi al secondo (348 m/s ca.). Secondo la teoria generale della propagazione delle onde di pressione in un mezzo elastico, la velocità del suono c avrebbe dovuto essere uguale alla radice quadrata di p/δ, dove p rappresenta la pressione e δ la densità del mezzo. Nel 1760 il matematico Joseph-Louis Lagrange (1736-1813) osservò che la discrepanza poteva essere eliminata qualora la pressione, invece di essere proporzionale alla densità (secondo la legge di Boyle), fosse proporzionale alla radice cubica di essa; tuttavia, lo stesso Lagrange non prese sul serio la propria congettura, poiché implicava un allontanamento dalla legge di Boyle troppo grande per essere sfuggito ai filosofi. Per uno scienziato ormai abituato alla teoria caloricistica dei gas non era però difficile trovare il modo di aumentare teoricamente la velocità del suono. Non per nulla, Biot avrebbe poi presentato l'approccio che ebbe successo come se fosse stato una questione di senso comune. Era evidente, disse, che un'onda sonora deve scaldare il mezzo che attraversa, altrimenti, al contrario di quanto indica l'esperienza, essa avrebbe dovuto produrre la condensazione di vapori saturi. Laplace fu forse il primo a suggerire questa risposta e Biot nel 1802 effettuò i calcoli sotto la sua guida.

Biot introdusse un parametro k che rappresentava l'aumento ulteriore di pressione ‒ rispetto a quello associato alla compressione sulla base della legge di Boyle ‒ prodotto dal riscaldamento adiabatico che si verificava in un'onda sonora. Riformulando la teoria della propagazione delle onde nel caso in cui k 0, si ottiene per la velocità del suono un valore maggiore di quello di Newton di un fattore (1+k)^1/2. Biot ricavò il valore di k da una serie di misurazioni effettuate per altri scopi. La teoria e gli esperimenti non si accordavano in modo brillante, perciò Laplace trovò un modo di ottenere k teoricamente. Il calore necessario per alzare la temperatura di un gas di una certa quantità Δ, mentre la sua pressione rimane costante, è maggiore di quello richiesto per far aumentare la temperatura dello stesso Δ quando il volume è costante. La scuola di Laplace considerava la quantità positiva (c_p−c_v)Δ, dove le c rappresentano i calori specifici nei due casi, come calore latente, poiché non influenzava il termometro. Laplace affermò che i processi di compressione e dilatazione che si hanno nella propagazione del suono avvengono in modo così rapido da non permettere a questo calore latente di uscire dal volume considerato; il suo effetto sul volume compresso si manifesta aumentandone la temperatura di Δ(c_p−c_v)/c_v. La correzione da apportare nell'equazione generale delle onde è appunto il coefficiente di Δ; così, k=(c_p/c_v)−1, da cui: k+1=c_p/c_v. Nonostante le oscurità nei passaggi dell'argomentazione e la scarsità dei dati usati per confermare la formula, quest'analisi risultò plausibile; di fatto, essa può essere riformulata in modo da soddisfare i criteri della termodinamica moderna.

Per inserire saldamente la velocità del suono, e quindi la teoria del calorico, nell'ambito della sua visione fisica, Laplace ricavò il fattore c_p/c_v da un modello basato su forze a corto raggio. In questo modello ciascuna molecola di gas è circondata da un'atmosfera di calorico; ne segue che esiste una certa repulsione fra la sua atmosfera e quella delle molecole vicine, e una certa attrazione fra essa e gli altri elementi e molecole circostanti. Ciascuna molecola perde continuamente parte della sua atmosfera a causa del bombardamento di calore radiante proveniente da altre molecole, ma cattura al contempo il calorico che le viaggia attorno, sicché nello stato stazionario il guadagno compensa la perdita. Il risultato di questa complessa visione fu una costante d'integrazione incalcolabile ed essa non fornì alcuna ulteriore informazione sul fluido calorico.

La luce e il calore

Anche se più volte sfidata, la teoria della luce dominante nel corso del XVIII sec. derivava dalla concezione newtoniana dei 'raggi' come fasci di particelle. La concezione opposta, ossia l'idea che la luce si propaga per onde in un particolare mezzo detto 'etere', come fa il suono nell'aria, aveva intorno al 1750 sostenitori importanti, come, per esempio, Benjamin Franklin (1706-1790) e Leonhard Euler (1707-1783). Tuttavia, prima della fine del secolo nessuno seppe tradurla in un'alternativa pienamente sviluppata al modello corpuscolare. Subito dopo il 1800 Thomas Young indicò il modo in cui un modello ondulatorio, capace d'incorporare il principio di sovrapposizione illustrato dal comportamento delle onde d'acqua, poteva rendere conto del fenomeno della diffrazione. Questi fenomeni, spiegati dalla teoria dei raggi in modo macchinoso, facendo riferimento a complicate configurazioni per le forze agenti fra le particelle di luce e le superfici diffrangenti, divennero il principale campo di battaglia di una disputa fra i seguaci di Young e i discepoli di Laplace. Le altre schermaglie riguardavano l'interpretazione della polarizzazione che Newton aveva inserito nel suo modello, supponendo che i raggi di luce non fossero sfericamente simmetrici, ma che avessero lati o facce differenti.

Mentre era in corso la battaglia sul modello di luce, gli esperimenti arricchirono notevolmente il campo dei fenomeni rilevanti. La scoperta del calore radiante ripropose ai filosofi la stessa domanda ‒ 'che cosa è la luce?' ‒ rendendo più acuto l'antico problema dei rapporti fra fuoco, luce e calore. Inizialmente la nozione di propagazione delle particelle di calorico s'inseriva nello schema generale degli imponderabili e, come i fenomeni di polarizzazione per riflessione scoperti da Malus nel 1810, sembrava favorire il modello balistico-materiale della luce. Con la vittoria della teoria ondulatoria, però, il calore radiante entrò nell'ambito dell'etere. Ben presto, verso la metà del XIX sec., anche il calore sarebbe rientrato nel modello dinamico seguito dall'elettricità e dal magnetismo, mentre la teoria degli imponderabili sarebbe del tutto scomparsa.

Durante il tardo Settecento molti filosofi naturali tentarono di misurare le proprietà delle ipotetiche particelle di luce; essi conoscevano, grazie alle osservazioni astronomiche, la grande velocità della luce. Se le particelle avevano una massa sensibile, la loro quantità di moto avrebbe dovuto essere misurabile. John Michell, sempre pronto a tentare gli esperimenti più delicati, appese a un perno una breve porzione di corda di clavicembalo, a un'estremità della quale era legato un piccolo pezzo di rame equilibrato da un contrappeso all'altra estremità. Quando focalizzò la luce sul rame, il filo si spostò dalla posizione di equilibrio. Dal movimento del filo e dalla velocità della luce Priestley, che nel 1772 aveva pubblicato il risultato di Michell, calcolò la quantità di materia trasportata ogni giorno dalla luce del Sole sulla superficie della Terra e, quindi, la corrispondente diminuzione giornaliera della sostanza solare. Il risultato di questo calcolo, che era di soli due grani (130 mg ca.), rassicurò i filosofi i quali avevano cominciato a temere che il Sole potesse consumarsi interamente prima della fine del mondo. La sensazione di sollievo, si rafforzò quando, vent'anni dopo, il grande misuratore Bennet eseguì un esperimento analogo con un filo d'oro sospeso da una tela di ragno e non ottenne alcun movimento che non potesse essere plausibilmente attribuito alle correnti d'aria causate dai raggi focalizzati del Sole.

Nel frattempo Michell escogitò un altro modo d'individuare la massa di una particella di luce. Partendo dal presupposto che tali particelle fossero soggette alla legge di gravità, egli calcolò che una stella densa come il nostro Sole, ma con una massa 155 volte più grande, avrebbe dovuto frenare una particella luminosa da essa emessa fino al 95% della velocità della luce solare; ciò avrebbe dovuto dare alla luce della stella un indice di rifrazione misurabile maggiore di quello della luce solare. Cavendish chiese a Maskelyne e a Herschel d'individuare questo effetto, ma, pur esaminando molte stelle, nessuna di esse parve essere dotata di una massa sufficiente a rallentare le particelle luminose di una quantità osservabile.

Anche i filosofi naturali della metà del Settecento pensarono di mettere in relazione la velocità della luce con il suo colore. Un giovane scozzese, Thomas Melvill (1726-1753), e un maturo francese, il marchese di Courtivron (1715-1785), quasi nel medesimo momento anche se indipendentemente l'uno dall'altro, ebbero la stessa idea. Essi pensarono che se le particelle di luce avessero avuto soltanto velocità diverse, le eclissi avrebbero dovuto manifestarsi in modo assai più evidente di quanto avveniva in realtà. Il rapporto degli indici noti di rifrazione del rosso e del viola dava un'indicazione sul rapporto tra velocità delle particelle corrispondenti; Melvill assegnò a tale rapporto il valore di 78/77 e Courtivron di 45/44; ciò implicava che i satelliti di Giove avrebbero dovuto cambiare colore per circa un minuto entrando o uscendo dall'ombra del pianeta. Osservazioni accurate non rilevarono però effetti di questo tipo.

Dietro la trascurabile differenza numerica fra le stime di Melvill e di Courtivron si nasconde il notevole livello di elaborazione della teoria materiale della luce. Melvill considerava il rapporto delle velocità come inversamente proporzionale al rapporto degli indici; Courtivron effettuò i suoi calcoli a partire dalla dinamica che supponeva fosse in gioco. Egli ragionò alla maniera del suo maestro Clairaut: se una particella di luce con velocità v si avvicina a una superficie rifrangente con un angolo d'incidenza φ, secondo la teoria balistica essa è attratta perpendicolarmente alla superficie da una forza a corto raggio che devia la sua traiettoria di un angolo di rifrazione θ (in base alla legge di Snell μsenθ=senφ, con μ indice di rifrazione del mezzo di propagazione); una volta entrata nel mezzo rifrangente, la particella prosegue il suo percorso con una nuova velocità w>v. L'accelerazione aumenta la vis viva della particella di una quantità uguale all'integrale della forza accelerante lungo il raggio di azione, sicché w²=v²+λ, dove λ rappresenta il valore dell'integrale, considerato come una costante della superficie. Poiché la componente della velocità della particella parallela alla superficie non cambia, senφ/senθ=w/v=μ; da ciò si ricava che v²(μ²−1)=λ, per cui l'osservatore dell'esperimento di Melvill e Courtivron avrebbe dovuto aspettarsi che (v_r/v_v)²=(μ_v²−1)/(μ_r²−1), dove i pedici r e v indicano, rispettivamente, il rosso e il viola.

è possibile ribaltare questa stessa analisi per ricavare l'indice di rifrazione nei termini di variabili dinamiche. Sembra questa la motivazione che guidò Robison quando, nel 1788, effettuò un calcolo simile a quello che abbiamo brevemente riportato. Anche Laplace riprodusse questa argomentazione nel suo caratteristico stile. Egli suppose che v_x e v_y indicassero le componenti, rispettivamente perpendicolare e parallela alla superficie, della velocità iniziale della particella e che la forza accelerante, X(x), agisse esclusivamente all'interno di una banda molto ristretta, di larghezza s da entrambi i lati della superficie; egli ottenne la velocità nella direzione x dopo il passaggio attraverso la banda di forza come V_2s²=V_s²+2I=v_x²+4I, dove I è l'integrale di X(x)dx da 0 a s. L'indice di rifrazione μ dipende esclusivamente da I e dalla velocità v della luce nel primo mezzo:

Questo risultato è lo stesso pubblicato sei anni prima da Clairaut, il quale si aspettava che ulteriori studi avrebbero portato a scoprire la forma della legge di forza, X(x), e i suoi limiti s, in modo da consentire il calcolo dell'integrale I. Questo risultato avrebbe fornito importanti informazioni sull'attrazione fra luce e materia. Invece, secondo Laplace, il valore di I non dipendeva dai particolari matematici della forza; non era possibile né calcolare I a partire da essi, né questi potevano essere ricavati da I, usando i valori noti di μ. La posizione di Laplace è nota: il raggio della forza X(x) è così piccolo che la dipendenza dalla distanza non conta. Il sistema di Laplace, come le forze che chiamava in causa, non poteva penetrare sensibilmente oltre la superficie delle cose.

Il modello delle particelle di luce in volo deflesse da forze a breve distanza continuò a essere presente nei dibattiti sui fenomeni ottici che avevano luogo nel circolo di Laplace, anche se non fu prodotto alcun lavoro di tipo quantitativo che richiedesse la conoscenza della legge di forza ipotizzata. Ciò vale anche per gli studi effettuati intorno al 1810 da Biot e Malus sulla doppia rifrazione e sulla polarizzazione. In nessuno dei due casi si fece appello alle forze (proprio come era avvenuto nella teoria del calore di Laplace, che non faceva uso di calcoli sulle atmosfere di calorico), né esse avrebbero potuto essere collegate ai dettagli dell'esperimento (come avveniva nel calcolo di Laplace degli indici di rifrazione). La scuola di Laplace metteva così in evidenza, in un modo che forse essa stessa non riconosceva, il carattere strumentale dei propri modelli fisici.

Il calore radiante

La scoperta, effettuata per mezzo degli specchi metallici, che il freddo così come il caldo potevano essere irradiati al pari della luce sollevò molte perplessità e condusse, alla fine, all'elaborazione di una brillante ipotesi teorica, la cosiddetta 'legge di scambio', formulata da Pierre Prévost (1751-1839), professore di filosofia naturale a Ginevra. Secondo questa teoria tutti i corpi irraggiano calorico, e i corpi caldi in misura maggiore di quelli freddi; una conseguenza è che la temperatura rilevata da un termometro è il risultato di uno scambio dinamico di calore con i corpi circostanti.

Secondo alcuni scienziati il concetto di scambio dinamico di calore radiante presentava alcuni problemi. Per Benjamin Thompson (1753-1814), un tory che fuggì dalle colonie inglesi in America e finì per diventare conte Rumford di Baviera, questo scambio non aveva alcun senso. Si trattava, egli disse, di "un'operazione non soltanto incomprensibile, ma apparentemente impossibile, per la quale non è dato di trovare alcunché di analogo che la possa rendere plausibile" (Works, I, p. 422). Nel 1802, relegato a Monaco, egli si dedicò a demolire la teoria di Prévost e a conquistare la mano della vedova di Lavoisier. Rumford respinse in blocco la teoria del calorico, contro la quale aveva già utilizzato il suo famoso esperimento sulla trapanazione dei cannoni. Questa situazione scottante si tradusse in un'opportunità straordinaria per la signora Lavoisier. "Credo" scrisse Rumford alla sua amante inglese "che vivrò per spazzar via la teoria del calorico, proprio come il defunto signor Lavoisier [l'autore del calorico] spazzò via il flogisto. Che destino singolare per la moglie di due filosofi!" (Brown 1979, pp. 255, 268).

Rumford riteneva che la propagazione del suono, e non quella della luce, dovesse essere il fenomeno parallelo al calore radiante. Un corpo caldo emette pulsazioni rapide, un corpo freddo pulsazioni più lente, e le radiazioni che essi emettono sono diverse proprio come le note acute sono differenti da quelle gravi. Rumford fu iniziato a questo genere d'idee intorno al 1800 a Londra da Humphry Davy (1778-1829) e Thomas Young, assistenti della Royal Institution, che era stata da poco fondata con il contributo dello stesso Rumford. Mentre Davy insegnava che il calore radiante nasce dalla spinta dei corpi caldi sull'etere, Young sviluppava la sua teoria ondulatoria della luce.

Nel tentativo di confutare Prévost, Rumford indagò il modo in cui il carattere della superficie dei radiatori influiva sulla loro efficienza. Egli scoprì, facendo uso di un termometro differenziale, chiamato 'termoscopio', che le superfici nere e ruvide irradiano più intensamente di quelle lisce e luminose e per questo cominciò a indossare un cappello lucido per conservare il calore della testa. Rumford avrebbe formato una strana coppia con John Leslie (1766-1832), il quale usava tingersi i capelli di un colore rosso purpureo. Rumford insistette sul fatto di non averlo mai incontrato quando, nel 1804, Leslie pubblicò la sua Experimental inquiry into the nature and propagation of heat. Qui egli asseriva di aver effettuato le misurazioni termoscopiche prima di Rumford, ma i suoi risultati derivavano da una tecnica che lo avrebbe portato a scontrarsi con un'autorità assai più formidabile di Rumford stesso.

Stiamo parlando di William Herschel (1738-1822), che godeva di una pensione offertagli dalla Corona per le sue scoperte astronomiche. Herschel non s'interessava, come Rumford e Leslie, del calore totale irradiato, quanto del calore associato ai sette colori dello spettro solare newtoniano. Per scoprire quale colore portasse più calore, egli proiettò uno a uno su un termometro i colori prismatici. Le prime prove mostravano che l'effetto di riscaldamento diminuiva in maniera monotona dal rosso al viola. Da ciò risultava che "il calore radiante, come la luce, che si tratti di differenti agenti o di uno soltanto, non solamente è soggetto a rifrazione, ma è anche soggetto alle leggi della dispersione quali derivano dai suoi differenti gradi di rifrangibilità". Herschel, in questa prima fase della ricerca, supponeva che il massimo effetto termico dovesse essere trasportato dai raggi con una rifrangibilità minore rispetto al rosso. "In questo caso il calore radiante consisterà in parte, se non principalmente, di luce invisibile, se mi si permette questa espressione, ossia di raggi che vengono dal Sole e che hanno una quantità di moto che li rende inadatti a essere percepiti con la vista" (The scientific papers of Sir William Herschel, II, pp. 53-56, 60, 63).

Rimaneva da chiarire se la luce e il calore derivassero dallo stesso agente o da agenti diversi. Per rispondere a tale questione, Herschel esaminò la trasmissione relativa dell'intero spettro della luce visibile e del calore radiante, avvalendosi di vari tipi di schermi. Una diminuzione nell'intensità della luce non corrispondeva a un decremento dell'effetto di riscaldamento. Secondo Herschel era chiara la conseguenza di ciò: la luce e il calore erano di natura diversa. Egli affermò che il filosofo che avesse voluto insistere sulla loro identità avrebbe dovuto restare legato alle "posizioni arbitrarie e inaccettabili" di chi sosteneva che, all'aumentare della rifrangibilità, i raggi di calore iniziano a svanire o a trasformarsi in luce (all'estremo rosso dello spettro), che l'illuminazione aumenta quando l'effetto di riscaldamento diminuisce e che sia l'illuminazione sia il calore svaniscono all'estremo limite del viola. Leslie non si oppose alla distinzione radicale di Herschel fra luce e calore, ma all'idea che il calore potesse esistere oltre lo spettro visibile. Egli dimostrò il contrario servendosi di un termometro differenziale costruito con un tipo di vetro attraverso il quale, a sua insaputa, non passavano i raggi infrarossi.

I sostenitori francesi del calorico, incerti se accodarsi all'una o all'altra delle autorità inglesi, riconsiderarono ogni cosa dal principio prima di cercare di gettar luce sul fenomeno del calore. Delaroche si prefisse di chiarire i fatti e Bérard s'impegnò a estenderli. Delaroche, nel suo articolo Observations sur le calorique rayonnant pubblicato nel 1812 sul "Journal de physique", stabilì che la trasmissione del potere di riscaldamento della luce attraverso una lastra di vetro aumenta con l'aumentare della temperatura e della luminosità del corpo emittente; inoltre, il passaggio dei raggi attraverso una seconda lastra diminuisce il loro effetto di riscaldamento molto meno di quanto avvenga nel primo passaggio. "Se il calorico è un fluido, questo fluido è lungi dall'essere composto da parti omogenee". Ma questi risultati non facevano che rafforzare l'analogia con la luce. "Chi potrà ‒ prosegue Delaroche ‒ astenersi dal vedere in questo fenomeno un argomento assai valido da aggiungere a quelli che hanno portato alcuni physiciens a considerare il calorico radiante una semplice modificazione della luce, o piuttosto la luce uno stato speciale del calorico?" (Observations, pp. 214-215).

In tal modo Delaroche, con cautela, pose la pietra tombale sullo schema degli imponderabili, proprio quando tale struttura iniziava a crollare, oseremmo dire, sotto il suo stesso peso.