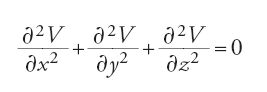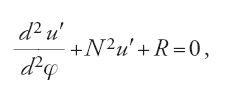L'Età dei Lumi: astronomia. L'astronomia del Sistema solare da Newton a Laplace
L'Eta dei Lumi: astronomia. L'astronomia del Sistema solare da Newton a Laplace
L'astronomia del Sistema solare da Newton a Laplace
L'astronomia nei 'Principia'
Nel novembre del 1785 e nei mesi di maggio e luglio dell'anno successivo Pierre-Simon de Laplace (1749-1827) presentò all'Académie Royale des Sciences di Parigi tre memorie, in cui erano chiarite per la prima volta alcune anomalie dei moti di Giove e di Saturno. A queste memorie fece seguito, nel dicembre del 1787, un lavoro volto espressamente a fornire una spiegazione dell'ultima anomalia irrisolta nel Sistema solare ‒ un'apparente accelerazione secolare del moto della Luna ‒ che risultò in seguito soltanto parzialmente corretta. Così, per Laplace e per i suoi contemporanei, proprio a distanza di un secolo dalla pubblicazione (1687) dei Principia di Newton, la legge della gravitazione universale si affermava come il principio necessario e sufficiente per calcolare i moti celesti con un'accuratezza dell'ordine di pochi secondi d'arco. L'astronomia era dunque divenuta la più esatta tra le scienze naturali. In quanto segue ci si propone di ricostruire il processo storico che portò a questo esito.
I Principia di Newton nacquero come ampliamento di un breve trattato, De motu, scritto su sollecitazione dell'astronomo Edmond Halley (1656-1742 ca.) e inviato alla Royal Society di Londra nel novembre del 1684. In questo trattato Newton si prefiggeva di dimostrare che i pianeti descrivono orbite ellittiche con il Sole in uno dei fuochi, e che i loro raggi vettori descrivono aree uguali in tempi uguali, esattamente come Johannes Kepler (1571-1630) aveva ipotizzato. Inoltre, egli proponeva di applicare le stesse leggi dinamiche al moto delle comete, al fine di determinare se alcune di esse avessero un moto periodico. Quest'ultimo problema si dimostrò particolarmente arduo, e solamente dopo il giugno del 1686 Newton riuscì a darne una soluzione.
In una prima revisione del De motu, risalente probabilmente al dicembre del 1684, Newton confrontò le forze di attrazione esercitate da Giove, Saturno, Terra e Sole, determinando le accelerazioni che tali corpi avrebbero impresso ai loro satelliti se questi fossero stati posti a una distanza fissa, la medesima per tutti. Egli fu così in grado di provare che il centro di gravità del Sistema solare si trova sempre nel Sole, o nelle sue vicinanze, il che gli consentì di "dimostrare l'ipotesi copernicana a priori". Generalizzando questi risultati, Newton concluse che tutti i corpi celesti esercitavano lo stesso tipo di attrazione; ne seguiva che il moto di ciascun pianeta era perturbato dai moti degli altri, sicché nessun pianeta avrebbe mai potuto descrivere esattamente la stessa orbita due volte. Il Sole attrae Giove, Giove attrae il Sole, la Terra attrae la Luna e la Luna la Terra (causando le maree e la precessione degli equinozi).
Come ebbe a scrivere Newton all'astronomo reale John Flamsteed (1646-1719), "ora che mi sto occupando di questo tema, mi piacerebbe andare in fondo alla questione prima di pubblicare i miei scritti" (Newton a Flamsteed, 12 gennaio 1685, Turnbull 1959-77). Dall'attrazione reciproca Newton dedusse che la forza attrattiva di ciascun corpo è proporzionale alla sua massa inerziale ed è la somma delle forze di attrazione delle sue particelle costituenti. Di conseguenza, la forza gravitazionale è presente in tutta la materia e dunque è una forza 'universale'. Affrontando le questioni che sorgevano via via nel corso dell'indagine, Newton ampliò il De motu dalle originarie 8 pagine manoscritte alle 510 della prima edizione a stampa dei Principia. Egli sapeva che la teoria della gravitazione universale avrebbe incontrato le resistenze dei filosofi naturali. I sostenitori del nuovo meccanicismo, guidati da René Descartes, sostenevano che tutte le forze agivano per contatto diretto e, secondo la teoria del moto planetario all'epoca più accreditata, i pianeti erano trasportati da vortici che si formavano nell'etere. Invece, a parere di Newton, essendo falliti tutti i tentativi di stabilire per via sperimentale le cause della gravitazione, era del tutto giustificata la decisione di non prendere posizione sull'argomento, "non definendo in questo trattato le specie o qualità fisiche delle forze, ma investigandone le quantità e le proporzioni matematiche" (Principia mathematica, scol. prop. I.69).
Nel Libro II dei Principia egli si propose di fondare una scienza dei moti dei solidi nei mezzi resistenti e di dimostrare che la teoria dei vortici non era in grado di spiegare i moti planetari. Le sue analisi erano nuove, ingegnose e talvolta erronee (la sua analisi dei vortici, per es., non teneva conto della condizione per l'equilibrio rotazionale). Le applicazioni newtoniane della teoria gravitazionale ai moti celesti erano spesso soltanto qualitative. Ne è un esempio la sua trattazione del problema dei tre corpi (prop. I.66), i cui risultati furono poi applicati alla Luna nel Libro III. Supponiamo che vi siano due corpi relativamente piccoli che ruotano intorno al loro baricentro comune, mentre quest'ultimo ruota intorno a un corpo distante e assai più grande, come, per esempio, il Sole. Newton dimostrò in termini qualitativi come la differenza variabile tra le accelerazioni causate dal Sole sulla Luna e sulla Terra determinasse le irregolarità nel moto della Luna: quelle note come 'variazione annuale' ed 'equazione annuale', le oscillazioni dell'eccentricità dell'orbita lunare e della linea degli apsidi postulate da Jeremiah Horrocks (1618-1641), le irregolarità latitudinali dei moti lunari scoperte da Tycho Brahe (1546-1601), il moto periodico nel senso diretto dell'apside lunare.
Nel Libro III Newton cercò di spiegare la forma della Terra e il moto di librazione della Luna, partendo dall'ipotesi che tali corpi celesti si fossero formati per condensazione da masse rotanti originariamente allo stato fluido; questa ipotesi avrebbe suscitato parecchie riserve da parte dei suoi successori nel XVIII secolo. Riconducendo la precessione degli equinozi all'attrazione esercitata dalla Luna e dal Sole sul rigonfiamento della Terra in corrispondenza del suo equatore, Newton ne offrì la prima spiegazione dinamica plausibile; la sua deduzione quantitativa era però profondamente carente, non essendo egli in possesso dei necessari concetti di dinamica rotazionale. Newton si rendeva conto che i moti di Saturno devono essere sensibilmente perturbati da Giove, ma le sue proposte allo scopo di spiegare queste perturbazioni ‒ consistenti nel collocare il fuoco dell'orbita di Saturno nel baricentro comune del Sole e di Giove, e nel postulare un'oscillazione della retta apsidale e dell'eccentricità di Saturno ‒ si rivelarono inadeguate. Flamsteed tentò per anni di ridurre le perturbazioni di Saturno e di Giove a oscillazioni periodiche causate reciprocamente dai due pianeti, ma alla fine si arrese. I Principia newtoniani, dunque, se da un lato offrivano nuove spiegazioni di numerosi fenomeni, dall'altro lato lasciavano irrisolti molti problemi.
Le reazioni iniziali destate dai Principia furono diverse nei vari paesi. Alcuni studiosi britannici, come il citato Halley, David Gregory (1659-1708) e John Keill (1671-1721), divennero accesi sostenitori della teoria newtoniana, mentre influenti pensatori continentali criticarono l'opera in quanto non riusciva a individuare la causa della gravitazione. Un anonimo recensore nel "Journal des Sçavans" (del 2 agosto 1688) giudicò arbitrario l'assunto newtoniano della mutua interazione gravitazionale tra i pianeti, deplorando il fatto che la meccanica newtoniana mancasse di un fondamento fisico. Nel Tentamen de motuum coelestium causis (1689), che Gottfried Wilhelm Leibniz (1646-1716) scrisse solamente dopo aver studiato le prime quaranta proposizioni dei Principia, si ribadiva che "i pianeti sono mossi dai loro eteri". Christiaan Huygens (1629-1695), pur ammettendo la validità di molte dimostrazioni newtoniane, rifiutò l'idea dell'azione a distanza e in una memoria del 1690, dal titolo Discours de la cause de la pesanteur, cercò di spiegare le forze centrali attraverso l'azione dell'etere. Nei dibattiti sul moto planetario del terzo decennio del Settecento la maggioranza degli studiosi continentali continuava a fare riferimento alla teoria dei vortici, cercando però nello stesso tempo di conciliare le teorie dell'etere con le principali conclusioni quantitative (come, per es., le cosiddette 'leggi di Kepler') che Newton era riuscito a dedurre. La teoria dei vortici sembrava adatta a spiegare il fatto che il moto intorno al Sole di tutti i pianeti avvenisse nella stessa direzione e quasi sullo stesso piano, ma lasciava senza risposta il problema delle inclinazioni delle orbite planetarie l'una rispetto all'altra. Per di più, le osservazioni raccolte da Halley dimostravano che le comete ruotano intorno al Sole in direzioni casuali e ciò era inconciliabile con la teoria dei vortici.
Nel corso del tempo, in luoghi diversi, anche nell'Europa continentale, i sostenitori dell'attrazione newtoniana cominciarono a rendere esplicite le loro posizioni. Per esempio, Willem Jacob 'sGravesande (1688-1742), professore all'Università di Leida negli anni Venti e Trenta del Settecento, rese popolare l'uso del termine 'legge' per fenomeni generalizzati mediante induzione, illustrando le sue lezioni per mezzo di dimostrazioni sperimentali. Nel 1738 Voltaire pubblicò ad Amsterdam gli Élémens de la philosophie de Neuton, mis à la portée de tout le monde, nei quali esponeva in forma divulgativa l'empirismo di Newton e le sue teorie ottiche e astronomiche. Nel primo trentennio del Settecento, inoltre, un gruppo di 'giovani newtoniani' cominciò a far sentire la propria voce anche nell'ambito dell'Académie Royale des Sciences di Parigi, per lungo tempo roccaforte delle teorie cartesiane.
La teoria lunare quantitativa
Il 1° settembre del 1694 Newton e Gregory fecero visita a Flamsteed nell'Osservatorio di Greenwich. Flamsteed mostrò a Newton circa 150 posizioni osservate della Luna, assieme alle corrispondenti posizioni previste dalla propria teoria lunare, formulata nel 1681 sulla base dei lavori di Horrocks, indicando inoltre gli errori delle longitudini calcolate, che in media erano dell'ordine di circa 8′ d'arco. Dalle osservazioni di Flamsteed, che oggi siamo in grado d'identificare, risulta che le misurazioni avevano un'accuratezza dell'ordine di 0,5′ d'arco. Flamsteed era stato nominato astronomo reale nel 1675, con lo stipendio di 100 sterline annue e con il compito di correggere le posizioni degli astri, nonché di osservare la Luna e i pianeti al fine di determinarne i moti con esattezza. L'obiettivo era di trovare un metodo che consentisse ai marinai di stabilire la longitudine in mare. Il metodo di chi si basava sul moto lunare comprendeva i seguenti passi: in primo luogo, occorreva determinare l'ora locale, ossia il numero di ore trascorse dal mezzogiorno locale; in secondo luogo, si trattava di definire la posizione della Luna con riferimento alla posizione nota di una stella e, infine, sulla base di tale posizione e di tavole lunari precise per un dato meridiano (per es., quello di Greenwich), si calcolava l'ora del giorno corrispondente al meridiano di riferimento. La longitudine della nave era data quindi dalla differenza tra il tempo locale e quello del meridiano di riferimento. Tale metodo presupponeva una notevole esattezza sia nella determinazione delle posizioni delle stelle fisse, sia nelle tavole lunari. Poiché la Luna ha in media una velocità di 13,18° (ossia 790,8′ d'arco) al giorno, mentre la Terra ruota di 360°, calcolare la differenza di longitudine dal meridiano di riferimento con un'approssimazione nei limiti di 1° presupponeva che le tavole lunari avessero un'accuratezza dell'ordine di 790,8′/360, ossia di circa 2,2′ d'arco.
Le tavole di Flamsteed non avevano, ovviamente, la precisione necessaria; Newton si assunse dunque il compito di sviluppare una teoria più accurata. L'anno successivo egli richiese ulteriori osservazioni a Flamsteed, il quale gliene fornì altre 100, per un totale di 250, costituenti l'insieme di osservazioni più esteso e accurato che uno studioso avesse mai avuto a disposizione per formulare una teoria lunare. Nel corso di questo periodo il carattere brusco di Newton e l'invidia di Flamsteed nei suoi confronti determinarono un progressivo deterioramento dei loro rapporti, che si ridussero in ultimo a una glaciale cortesia. Newton pubblicò nel 1702 la sua versione modificata della teoria di Horrocks, senza mai menzionare Flamsteed, dapprima in latino negli Astronomiae physicae et geometricae elementa di Gregory e successivamente in inglese con il titolo A new and most accurate theory of the Moon's motion.
Gli elementi della teoria sono presentati senza alcuna indicazione riguardo il modo in cui erano stati ottenuti. Nuovi valori sono assegnati ai coefficienti dell'equazione annuale della Luna, alla variazione e alle oscillazioni previste da Horrocks dell'eccentricità dell'orbita e della retta apsidale. Per la prima volta sono assegnate equazioni annuali speciali ai moti medi del nodo e degli apsidi lunari, i cui valori massimi sono rispettivamente di 20′ e di 9′30″. La teoria include altresì quattro nuovi piccoli termini o 'equazioni'. Indicando con S, A, N rispettivamente le posizioni del Sole, dell'apogeo e del nodo lunare, si possono rappresentare i primi due con 3′45″sen[2(A−S)] e 47″sen[2(N−S)], dove i coefficienti sono valori medi, che vanno modificati in base a un'equazione annua nel corso dell'anno solare. Indicando con H l'afelio dell'orbita terrestre e con M la posizione della Luna parzialmente 'eguagliata' (ossia, la posizione media parzialmente corretta), il terzo dei piccoli termini risulta essere 2′10″sen(S−M+A−H); il segno qui dovrebbe essere però negativo, e nella seconda edizione dei Principia (1713) il coefficiente fu corretto in −2′25″ (scol. prop. III.35). Come quarto termine si ha 2′20″sen(S−M). Nella seconda edizione dei Principia, Newton affermò ‒ senza fornire spiegazioni ‒ che queste equazioni erano state derivate dalla teoria gravitazionale.
La validità dei quattro piccoli termini fu per lungo tempo messa in discussione, ma uno studio recente ha dimostrato che, tenendone conto, l'accuratezza della teoria aumenta sensibilmente. Un altro importante contributo in questo senso è rappresentato da un suggerimento di Halley che Newton incluse nella teoria, considerando l'eccentricità sulla retta apsidale istantanea, anziché proiettarla sulla linea media degli apsidi, come aveva fatto invece Flamsteed. Tuttavia, la nuova teoria non possedeva la precisione vantata nel titolo dell'edizione inglese. Nella versione riveduta che appare nella seconda edizione dei Principia, la teoria newtoniana mostra una deviazione standard di 1,9′ d'arco rispetto a una teoria moderna precisa; conseguentemente, il 95% dei suoi valori si discosta da quelli corretti per non più di 3,8′ d'arco (una volta che sia emendata dalla lieve imprecisione relativa al moto medio). Gli errori nella teoria horrocksiana formulata da Flamsteed del 1681 erano circa due volte più grandi.
Trascorse molto tempo prima che apparissero tavole lunari basate sulla teoria di Newton. Joseph-Nicholas Delisle (1688-1768) costruì tavole di questo tipo nel 1717, ma rinunciò a pubblicarle non essendo riuscito a destare l'interesse dei colleghi dell'Académie Royale des Sciences e avendo appreso che le tavole lunari di Halley erano già in stampa, sebbene non ancora pubblicate. Le prime tavole lunari newtoniane furono pubblicate nella Uranoscopia (1735) di Charles Leadbetter, mentre quelle contenute nelle Institutions astronomiques (1746) di Pierre-Charles Le Monnier (1715-1799) rappresentano un caso particolare; originariamente compilate da Flamsteed tra il 1702 e il 1703, esse giunsero per vie a noi ignote nelle mani di Le Monnier, che v'incorporò i perfezionamenti introdotti nella seconda edizione dei Principia, adattandole al meridiano di Parigi. Nel 1754 Jean-Baptiste Le Rond d'Alembert (1717-1783) si servì delle tavole di Le Monnier come termine di paragone per dimostrare come la propria teoria e altre derivate analiticamente segnassero un progresso rispetto a quella newtoniana.
Ignorando in quale modo Newton avesse ottenuto le costanti della propria teoria, i suoi successori non furono in grado di rifare la derivazione. Halley, tuttavia, propose un metodo che consentiva di determinare la longitudine lunare con una precisione maggiore rispetto a Newton. Le discrepanze tra teoria e osservazione si sarebbero dovute determinare nell'arco di un cosiddetto 'ciclo di Saros' ‒ un periodo corrispondente a 223 lunazioni (poco più di 18 anni) ‒ trascorso il quale le configurazioni del Sole, della Luna e della Terra si ripetono quasi esattamente. Nel 1720, dopo aver assunto la carica di astronomo reale ricoperta in precedenza da Flamsteed, Halley si accinse a realizzare questo progetto. All'epoca della sua morte (1743) egli aveva registrato le discrepanze tra la longitudine osservata e quella calcolata nell'arco di un periodo più lungo di un ciclo di Saros completo; le sue tavole e le sue comparazioni furono pubblicate postume, nel 1749. Da un ciclo di Saros al successivo le divergenze tra l'osservazione e la teoria di Newton (una volta apportate le correzioni relative ai moti medi) si ripetono con una precisione di circa 1′ d'arco. Il problema della longitudine poteva quindi essere risolto utilizzando il metodo di Halley.
La controversia sulla forma della Terra
Nel 1672 l'Académie Royale des Sciences di Parigi incaricò uno dei propri osservatori, Jean Richer, di effettuare una spedizione astronomica alla Caienna, un'isola al largo della Guiana Francese, circa 5° a nord dell'equatore. Richer portò con sé un pendolo che era stato regolato a Parigi; sull'isola questo risultò perdere 2,5 minuti al giorno e dovette essere accorciato di 1,25 linee di un piede di Parigi (corrispondenti a circa 2,8 mm). Dieci anni più tardi Jean Deshayes e M. Varin confermarono il risultato di Richer attraverso osservazioni condotte nelle isole di Capo Verde.
Newton cercò di spiegare il fenomeno nelle proposizioni III.19 e III.20 dei Principia. In una sfera omogenea soggetta alla forza di gravità, l'attrazione è la stessa su ogni punto della superficie; ma se la sfera è in rotazione, la gravità effettiva all'equatore è data dall'attrazione gravitazionale meno la forza centrifuga dovuta alla rotazione ed è quindi minore della gravità effettiva al polo. Partendo dalla velocità di rotazione della Terra e dall'attrazione gravitazionale determinata attraverso gli esperimenti con il pendolo, Newton (assumendo la Terra come sferica) dimostrò che la forza centrifuga all'equatore è 1/289 dell'attrazione di gravità, senza variazioni apprezzabili se la sfera presenta uno schiacciamento molto piccolo. Una Terra omogenea e originariamente allo stato fluido avrebbe, secondo Newton, raggiunto all'equilibrio la forma di un ellissoide di rotazione schiacciato, in rotazione attorno al suo asse polare. Egli sosteneva che se la materia della Terra fosse stata suddivisa in colonne rettilinee estendentisi dal centro alla superficie, esse avrebbero avuto tutte lo stesso peso. Sulla base di queste ipotesi, Newton dimostrò che l''ellitticità' o schiacciamento (re−rp)/rp, dove re è il raggio equatoriale e rp il raggio polare, è pari a 1/229.
Gli studiosi successivi trovarono sconcertanti le teorie di Newton. Sulla base di quali presupposti si poteva affermare che la forma della Terra è ellissoidale ed è una figura di equilibrio? Poteva la dimostrazione applicarsi anche a forme con uno schiacciamento finito anziché infinitesimale? Le osservazioni di Giove condotte da Flamsteed e da Gian Domenico Cassini (1625-1712) dimostravano che il pianeta era troppo schiacciato ai poli perché vi si potesse applicare la teoria newtoniana. Newton suggerì di spiegare la differenza assumendo che Giove non fosse omogeneo e presentasse una maggiore densità al centro o verso l'equatore, ma non fornì alcuna dimostrazione al riguardo. Nel 1690 apparve l'opera Discours de la cause de la pesanteur di Huygens, nella quale la gravità era considerata una forza costante diretta verso il centro della Terra, causata dalla pressione dell'etere. Al pari di Newton, Huygens trovò che la forza centrifuga per unità di massa è, all'equatore, 1/289 della forza di gravità e riprese il principio delle colonne lineari bilanciate (considerandolo equivalente al principio secondo cui la superficie è ovunque perpendicolare al filo a piombo); applicando, però, la sua teoria della gravità, pervenne a un grado di appiattimento inferiore (1/578).
Nel 1718 Jacques Cassini (1677-1756), figlio di Gian Domenico, completò la misurazione del meridiano di Parigi che era stata iniziata quasi mezzo secolo prima da Jean Picard, e annunciò che un grado di latitudine a nord di Parigi era più corto di un grado di latitudine a sud (la differenza era di 265 m, essendo un grado di latitudine qui equivalente a poco più di 111 km). La Terra, concluse Cassini, è allungata ai poli, ossia è un ellissoide di rotazione allungato.
Delisle fu uno dei pochi sostenitori dei Principia newtoniani all'Académie Royale des Sciences in quegli anni. Ricordiamo come in precedenza, scoraggiato dai colleghi, egli avesse rinunciato a pubblicare le sue tavole lunari secondo le indicazioni newtoniane. In sede privata, Delisle avanzò l'ipotesi che la piccola eccedenza nella lunghezza del grado di latitudine astronomica a sud di Parigi, rilevata da Cassini, potesse essere scaturita da un errore di osservazione. Un modo migliore per determinare la forma della Terra, a suo avviso, sarebbe stato quello di misurare gradi di longitudine a differenti latitudini. I suoi tentativi in questo senso peraltro si dimostrarono infruttuosi. D'altra parte, l'Académie di Parigi all'epoca era molto attenta a soffocare espressioni pubbliche di dissenso tra i suoi membri. Nel 1725 Delisle accettò l'invito di Pietro il Grande, che gli propose di dirigere un nuovo osservatorio astronomico a Pietroburgo, dove rimase sino al 1747.
Sia la geodesia empirica sia la teoria newtoniana conobbero una rinascita a Parigi negli anni Trenta del Settecento, soprattutto grazie agli sforzi di Pierre-Louis Moreau de Maupertuis (1698-1759), ma i progressi in questi due campi non furono strettamente legati né sul piano politico né sul piano logico. Nel 1724 Giovanni Poleni (1683-1761), professore di astronomia, di filosofia e di matematica dell'Università di Padova, aveva pubblicato un trattato dal titolo Epistolae duae, in quarum altera proponuntur nonnulla de telluris forma in cui, indipendentemente da Delisle, metteva in discussione il fatto che le misurazioni di Cassini potessero far concludere alcunché in merito all'elongazione della Terra, e proponeva di determinare la forma del pianeta attraverso misurazioni di gradi di longitudine a differenti latitudini. Il trattato in questione fu ripubblicato nel 1729 con il titolo Epistolarum mathematicarum fasciculus e recensito in una rivista olandese nel 1733. Pierre-Louis Moreau de Maupertuis, membro dell'Académie di Parigi e poi presidente della classe di scienze fisiche della Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino, si basò su tale recensione in una memoria del giugno del 1733 (Sur la figure de la terre), in cui sollecitava un rinnovato sforzo per determinare empiricamente la forma della Terra; a tale sforzo, sottolineava Maupertuis, doveva essere data la precedenza sulle discussioni meramente speculative. Su questo punto potevano trovarsi concordi anche studiosi con opinioni per altri versi divergenti. Fu deciso, infine, di misurare i gradi di latitudine piuttosto che di longitudine, in quanto la determinazione di quest'ultima era ancora troppo imprecisa. Furono inviate due spedizioni, una al circolo polare in Lapponia e l'altra all'equatore in Perù. La notevole differenza di latitudine avrebbe dimostrato se ai poli la Terra è schiacciata oppure allungata. La spedizione peruviana, guidata dai geodeti Louis Godin (1704-1760), Charles-Marie de La Condamine (1701-1774) e Pierre Bouguer (1698-1758), partì nel 1735, ma a causa dei dissensi insorti tra i responsabili e di difficoltà di altro tipo, portò a termine la sua missione solamente negli anni Quaranta; Bouguer fece ritorno in Francia nel 1744, La Condamine nel 1745, Godin nel 1751. La spedizione lappone, guidata da Maupertuis, partì nel 1736 e fece ritorno nel 1737. Il grado di latitudine misurato in Lapponia si dimostrò più lungo degli archi di meridiano misurati in precedenza in Francia. Sul frontespizio della sua relazione Maupertuis (sempre pronto a farsi pubblicità) aveva posto un'illustrazione che lo raffigurava nell'atto di schiacciare un globo terrestre. Una misurazione del meridiano di Parigi effettuata da Nicolas-Louis de Lacaille e da César-François Cassini de Thury nel 1739-1740 confermava che la Terra non è un ellissoide allungato bensì schiacciato ai poli, e allo stesso risultato pervennero successivamente le relazioni indipendenti di Bouguer e di La Condamine sulla base delle misure ottenute in Perù. Le misurazioni effettuate alle basse e medie latitudini, confrontate con la misurazione lappone, portarono però a risultati contrastanti per quanto concerne l'entità dello schiacciamento.
In numerose memorie, presentate tra il 1732 e il 1735, Maupertuis si propose di tradurre la teoria newtoniana sulla forma della Terra nel linguaggio algoritmico continentale, dando così avvio a una discussione molto tecnica. I risultati di Maupertuis erano inficiati da errori grossolani e non riuscirono a chiarire gli assunti non spiegati della teoria newtoniana. Tuttavia, in qualità di guida dei 'giovani newtoniani' all'interno dell'Académie di Parigi, Maupertuis continuava a sostenerne la causa e non è un caso se i primi progressi teorici si dovettero a un altro rappresentante dei giovani newtoniani dell'Académie, Alexis-Claude Clairaut (1713-1765).
Il primo scritto di Clairaut sulla teoria di Newton, portato a termine durante il soggiorno in Lapponia, fu pubblicato nelle "Philosophical Transactions" della Royal Society di Londra degli anni 1737-1738. Procedendo analiticamente in base all'assunto che la Terra è un ellissoide di rotazione omogeneo con uno schiacciamento infinitesimale, Clairaut dimostrò che se il rapporto tra la gravità effettiva all'equatore e quella al polo è proporzionale al rapporto tra il raggio polare e il raggio equatoriale, allora i valori effettivi della gravità a tutte le latitudini sono inversamente proporzionali ai raggi corrispondenti, come aveva affermato Newton. Era pertanto possibile che un ellissoide di rotazione omogeneo con uno schiacciamento infinitesimale fosse la configurazione di equilibrio. Le approssimazioni condurrebbero agli stessi risultati per ogni forma quasi sferica, ellissoidale o meno, con un grado di schiacciamento δ tale che δ2≪δ. Dalla misurazione lappone confrontata con quelle francesi risultava però uno schiacciamento di 1/177, maggiore di quello (1/229) calcolato da Newton; inoltre, l'aumento della gravità effettiva dall'equatore al polo era risultato superiore a quanto implicasse l'ellissoide omogeneo newtoniano. Partendo dall'affermazione di Newton secondo cui un corpo più denso verso il centro deve essere più schiacciato di quanto non accada per un corpo omogeneo, in una memoria del 1738 Clairaut formulò l'ipotesi che la Terra fosse formata da singoli strati ellissoidali omogenei aventi tutti lo stesso schiacciamento infinitesimale, ma con densità variabile dal centro alla superficie, e ne dedusse le conseguenze. Egli concluse che il maggior incremento della gravità effettiva dall'equatore al polo poteva essere spiegato ricorrendo all'ipotesi che la Terra fosse più densa al centro, ma in questo caso il suo modello implicava uno schiacciamento inferiore rispetto a quello con densità omogenea. Ne dedusse che Newton aveva seguito un modello differente per quanto riguarda la struttura interna e la variazione di densità della Terra.
Nel 1741 Clairaut apprese da uno scambio epistolare con il matematico scozzese Colin Maclaurin (1698-1746) che questi aveva calcolato, per una figura ellissoidale di rotazione stratificata, uno schiacciamento di 1/179 e un aumento della gravità effettiva dall'equatore al polo di 1/220, e questi valori erano entrambi maggiori di quello di 1/229 trovato da Newton. Avendo ricevuto lo scritto di Maclaurin A treatise of fluxions (1742), che conteneva uno studio geometrico (e non analitico) delle figure di equilibrio ellissoidali, Clairaut trovò altre discrepanze con i propri risultati. Al fine di darne una spiegazione egli intraprese un'analisi più approfondita del problema, che approdò nella Théorie de la figure de la terre tirée des principes de l'hydrostatique (1743). Alla fine, l'approccio geometrico di Maclaurin si sarebbe dimostrato di efficacia limitata; il futuro era nell'approccio analitico di cui Clairaut fu pioniere.
Una significativa innovazione della Théorie di Clairaut fu l'introduzione di una nuova condizione necessaria per l'equilibrio di una figura in rotazione; per esprimerla in forma analitica occorrevano però nuovi concetti matematici. Per ogni canale chiuso, di forma qualsiasi, all'interno del solido, l'equilibrio implica che lo sforzo totale (oggi diremmo il 'lavoro per unità di massa') misurato lungo un percorso chiuso deve essere pari a zero. Analogamente deve essere uguale a zero lo sforzo totale, calcolato per un canale di qualsiasi forma che va da un punto a un altro della superficie. In questo modo Clairaut dava un'espressione quantitativa al concetto di campo di forza conservativo, facendo ricorso agli integrali di linea al fine di formulare con esattezza il nuovo principio. La condizione necessaria perché un integrale di questo tipo sia integrabile (ossia che l'integrando sia un differenziale esatto) era già stata definita in precedenza in uno scambio epistolare tra Clairaut e Alexis Fontaine des Bertins (1704-1771), cultore di matematica e socio dell'Académie Royale des Sciences; tale condizione, per un integrando in due dimensioni, Pdx+Qdy, consiste nel richiedere che ∂P/∂y=∂Q/∂x.
Quanto alla forma della Terra, Clairaut dimostrò che, contrariamente a quanto affermato da Newton, una maggiore densità al centro non implica necessariamente uno schiacciamento maggiore rispetto a un solido omogeneo. Per una figura fluida di equilibrio che formi un ellissoide di rotazione schiacciato e sia costituita da un numero finito di strati concentrici omogenei, con gradi infinitesimali di schiacciamento, Clairaut stabilì che per la legge dell'inverso del quadrato il grado di schiacciamento δ deve essere tale che 1/576≤δ≤1/230, quando il rapporto tra forza centrifuga e gravità all'equatore ha il valore che assume nel caso della Terra, ossia 1/288. Clairaut trovò impossibile armonizzare una teoria matematica delle forme di figure di rotazione eterogenee con le ipotesi di Newton. A suo avviso, il grado di schiacciamento minore di 1/230 era imputabile con tutta probabilità a un errore nella misura del grado di latitudine in Lapponia: un'ipotesi che si rivelò profetica. Nel 1743, però, Clairaut aveva cominciato a dubitare che la legge della gravitazione universale potesse essere adeguatamente verificata attraverso misure geodetiche. D'Alembert criticò aspramente il trattato di Clairaut sulla forma della Terra, come del resto le sue principali ricerche matematiche, e cercò di risolvere il problema senza limitarsi alle forme ellissoidali omogenee e stratificate; i suoi tentativi non ebbero però successo, talché i risultati osservativi restavano inesplicabili.
Il dibattito fu riacceso da Adrien-Marie Legendre (1752-1833) in una memoria inviata nel 1782 all'Académie, Recherches sur l'attraction des sphéroïdes, in cui dimostrava che se la forza di attrazione di un solido di rotazione è nota per ogni punto esterno sul prolungamento del suo asse, sarà nota per qualsivoglia punto esterno. Per calcolare l'integrale che fornisce la forza di attrazione, Legendre sviluppò l'integrando in serie di potenze della frazione r′/r, dove r′ è il raggio vettore dal centro del corpo a uno dei suoi punti che esercitano l'attrazione e r il raggio vettore dallo stesso centro verso il punto esterno che subisce la forza di attrazione; i coefficienti nelle serie erano funzioni razionali intere, Pn, di cosγ, dove γ è l'angolo tra r e r′. I coefficienti Pn sono noti oggi come 'polinomi di Legendre', o anche come 'coefficienti di Laplace', o 'armonici zonali'. Il valore dell'integrale dipende dalla forma del solido, e quindi dalla curva formata dal meridiano.
Legendre all'epoca non era ancora membro dell'Académie. Laplace, incaricato di esaminare il suo contributo, gli suggerì l'idea della funzione potenziale, dalle cui derivate parziali può essere calcolata la componente della forza in ogni direzione (Laplace aveva a sua volta appreso l'efficacia di questo metodo dagli scritti di Lagrange). Utilizzando tale suggerimento, Legendre ottenne un'espressione per la funzione potenziale in termini dei polinomi che da lui avrebbero preso il nome. In uno scritto del 1784 Legendre applicò la condizione di equilibrio di una massa fluida rotante e, usando una serie di proprietà dei suoi polinomi, ottenne l'equazione per la curva meridiana. Laplace in seguito generalizzò il problema estendendolo dalle figure di rotazione a uno sferoide arbitrario, ossia a qualunque superficie data da un'equazione nella distanza r dal centro, nella longitudine λ e nella latitudine φ. Egli dimostrò che il potenziale V soddisfa un'equazione differenziale alle derivate parziali; espressa in coordinate cartesiane ortogonali, questa risulta essere:
nota oggi come 'equazione di Laplace'. Legendre dimostrò poi che V può essere espresso mediante la serie:
[2] V(r,λ,φ)=(U0/r)+(U1/r2)+(U2/r3)+...+(Un/rn+1),
dove le Un, note come 'funzioni sferiche' o 'funzioni armoniche', sono espresse in termini di polinomi di Legendre.
In una serie di memorie successive e nel secondo volume della Mécanique céleste (1799) Laplace tornò sul problema di conciliare teoria e osservazione. Gli esperimenti eseguiti con un pendolo a differenti latitudini dimostravano che lo schiacciamento terrestre era minore di 1/229, il valore calcolato da Newton per una Terra omogenea. La variazione totale della lunghezza del pendolo, dall'equatore al polo, risultava essere di 5,24 mm circa. Sulla base di quindici misurazioni a differenti latitudini, Laplace si propose di trovare un valore estremamente probabile dello schiacciamento terrestre, assumendo che il meridiano fosse ellittico, che gli errori per eccesso e per difetto avessero per somma zero e che la somma dei loro valori assoluti fosse minima. Egli ottenne un valore di 1/336; il suo calcolo, se correttamente eseguito, avrebbe dovuto dare 1/315. Nel 1832 Nathaniel Bowditch, traduttore della Mécanique céleste in inglese, servendosi di 52 misure a sua disposizione e utilizzando il metodo dei minimi quadrati ottenne un valore di 1/297, che concorda con quello attualmente accettato.
Nel 1799 Laplace poteva disporre di sette misure del meridiano a differenti latitudini. Determinando l'ellissoide più probabile, egli trovò uno schiacciamento pari a 1/312 e un errore nella misurazione in Lapponia di 336 metri. Ritenendo impossibile un errore così vistoso, Laplace arrivò alla conclusione che lo scostamento dall'ellitticità è tutt'altro che trascurabile. Negli anni 1801-1803, l'astronomo svedese Jöns Svanberg (1771-1851) effettuò una nuova misurazione dell'arco di meridiano lappone, che risultò essere di ben 390 m più corto rispetto alla lunghezza rilevata da Maupertuis. Gli scostamenti dalla forma ellissoidale si rivelarono sufficientemente piccoli da permettere di assumere come prima approssimazione della forma della Terra un ellissoide rotondo, il cosiddetto 'geoide' di riferimento. In seguito la geodesia si è proposta di determinare gli scostamenti dal geoide di riferimento causati da anomalie nella distribuzione della massa terrestre.
La trasformazione della meccanica celeste in analisi applicata
Nel primo decennio del Settecento sorse una controversia tra Newton e i leibniziani sulla priorità dell'invenzione di quello che Leibniz chiamava 'calcolo differenziale' e Newton 'metodo delle flussioni'. Nel 1713 apparve a Londra un pamphlet intitolato Commercium epistolicum, di cui Newton curò anonimamente il commento, dove si cercava di dimostrare che era stato Newton a suggerire a Leibniz l'idea del calcolo differenziale in uno scambio epistolare risalente a quarant'anni prima (in realtà, Newton e Leibniz scoprirono il teorema fondamentale del calcolo infinitesimale in modo indipendente, anche se la scoperta di Newton precedette quella di Leibniz). In una recensione anonima del pamphlet in questione ‒ in verità scritta da Newton e pubblicata nel numero di gennaio-febbraio del 1715 delle "Philosophical Transactions" ‒ si legge l'affermazione seguente: "Con l'ausilio della nuova analisi il signor Newton scoprì la maggior parte delle proposizioni dei suoi Principia. Ma poiché gli Antichi consideravano certo e ammettevano nella geometria soltanto ciò che era stato dimostrato sinteticamente, egli dimostrò le proposizioni sinteticamente affinché il sistema celeste potesse essere fondato su una buona geometria" (29, p. 206).
Questa dichiarazione, mirata a sostenere la priorità di Newton nella scoperta del calcolo infinitesimale, ingenerò la convinzione che egli avesse formulato le proposizioni dei Principia in forma algebrica, sostituendo in un secondo tempo lo sviluppo analitico con dimostrazioni geometriche. Tale era, per esempio, l'opinione di Laplace. Tuttavia, sulla base di uno studio approfondito dei manoscritti, Derek Thomas Whiteside ha concluso che "i Principia furono per la maggior parte 'inventati' nella stessa forma rigorosamente geometrica in cui furono 'composti' per la stampa" (Whiteside 1974, VI, p. 599). Soltanto nel caso di alcune proposizioni ‒ per esempio le I.39, 40, 45 e III.28 ‒ è probabile che Newton si basasse su risultati ottenuti precedentemente con un procedimento algebrico. Nel nuovo calcolo che appare nelle prime diciassette proposizioni del Libro I e in quelle iniziali del Libro III, che insieme formano il cuore dei Principia, non v'è traccia di fluenti o di flussioni oppure del loro rapporto inverso. Alle dimostrazioni geometriche si associa il 'metodo delle prime e ultime ragioni', in cui i limiti di rapporti di quantità sono calcolati facendo tendere a zero le quantità stesse.
Newton non fondò alcuna scuola matematica, ma vi furono alcuni seguaci che cercarono di usare i metodi newtoniani per estendere i suoi risultati o per colmare alcune lacune nelle dimostrazioni; È quanto fecero, per esempio, il vescovo Charles Walmesley (1721-1797) e il matematico Thomas Simpson (1710-1761) per la teoria lunare e per il problema della precessione degli equinozi, ma i loro sforzi furono resi vani da gravi manchevolezze. Il futuro era in un approccio algoritmico che consentisse di tenere distinti differenti ordini di approssimazione e di formulare e applicare principî di meccanica di ordine superiore. Era stato Leibniz a cercare sin dall'inizio un metodo unitario e puramente simbolico di risoluzione dei problemi e i suoi seguaci continuarono in questa direzione. Il ricorso al ragionamento diretto o alle figure geometriche andò declinando, fino a scomparire del tutto nella Méchanique analitique (1788) di Lagrange, che, come ebbe a vantare l'autore, non conteneva nemmeno una figura. L'attenzione si spostò verso le funzioni matematiche espresse simbolicamente.
L'uso del calcolo leibniziano per formulare problemi di meccanica iniziò con le memorie di Pierre Varignon (1654-1722), in cui si dimostrava, per esempio, che fdx=vdv, dove f è una forza di accelerazione, dx una distanza minima e v la velocità del corpo su cui agisce la forza; l'integrale per un corpo che parte dallo stato di quiete è ∫fdx=v2/2, dove v è la velocità finale raggiunta. Questo risultato è equivalente alla proposizione I.39 dimostrata geometricamente nei Principia newtoniani. Analogamente, Varignon utilizzò il calcolo leibniziano per dimostrare la deduzione di Newton secondo la quale il moto in un'orbita ellittica in cui il raggio vettore descrive, in tempi uguali, aree uguali intorno a un fuoco implica una forza centripeta inversamente proporzionale al quadrato della distanza. Quando però Leibniz chiese a Varignon di considerare le interazioni fra tre corpi ‒ come è fatto nella proposizione I.66 dei Principia ‒ egli non fu in grado di formulare il problema analiticamente se non assumendo il terzo corpo come immobile.
Nel 1710, Jacob Hermann (1678-1733) e Johann I Bernoulli (1667-1748), entrambi professori di matematica in varie università europee, usando il calcolo leibniziano dimostrarono che una forza centripeta inversamente proporzionale al quadrato delle distanze implica che l'orbita descritta sia una sezione conica. Nella prima edizione dei Principia Newton aveva enunciato questa legge nel primo corollario della proposizione I.13 senza darne dimostrazione, sebbene essa abbia un'importanza cruciale nella sua teoria (nella seconda edizione dell'opera è fornito però un abbozzo di dimostrazione). Sia Hermann sia Bernoulli si basarono su una traduzione in termini di calcolo differenziale della proposizione I.41 dei Principia.
Nel 1736 apparve la Mechanica del grande matematico Leonhard Euler (1707-1783), che fu membro dell'Academia Scientiarum Imperialis Petropolitana dal 1727 al 1741, dell'Accademia Reale Prussiana delle Scienze di Berlino dal 1741 al 1766 e di nuovo di quella di Pietroburgo dal 1766 sino alla sua morte. In quest'opera Euler usa sia il calcolo differenziale sia quello integrale, appreso da Johann Bernoulli, per una trattazione sistematica dei problemi relativi all'azione di forze su corpi che si muovono nel vuoto o in mezzi resistenti. Tuttavia egli non affronta il problema dei tre corpi, essenziale per l'applicazione della meccanica ai moti dei corpi celesti. Per spiegare questa lacuna, occorre tenere presente che nel primo trentennio del Settecento, al pari della maggioranza dei filosofi naturali dell'Europa continentale, Euler rifiutava l'idea dell'azione a distanza. Roger Cotes (1682-1716) nella sua prefazione alla seconda edizione dei Principia aveva lasciato intendere che l'attrazione gravitazionale costituisce una proprietà essenziale della materia, ed Euler attribuiva erroneamente la stessa convinzione a Newton e ai filosofi inglesi in generale. Euler si oppose a questa idea nei suoi scritti risalenti agli anni Quaranta-Sessanta, epoca in cui riteneva ancora che tutte le forze fossero di contatto e, al pari di molti altri, sosteneva la teoria dei vortici. Agli inizi degli anni Quaranta, persuaso da Daniel Bernoulli che tale teoria fosse inconciliabile con la legge dell'inverso del quadrato della distanza, Euler adottò l'ipotesi 'idrodinamica' formulata da questi nel 1738, secondo la quale la causa delle forze gravitazionali andava ricercata nelle differenze di pressione dell'etere determinate da differenze di velocità. Negli anni successivi, a quanto sembra, Euler abbandonò ogni tentativo di formulare ipotesi sulle cause della gravità, sebbene restasse convinto che l'etere fosse necessario per spiegare i fenomeni ottici.
Lasciando da parte le cause della gravitazione, il problema delle perturbazioni non poteva non imporsi all'attenzione di Euler per l'importanza e l'interesse che rivestiva. Negli anni Trenta, a quanto sembra, egli pensava che i moti planetari potessero essere calcolati unicamente sulla base di una forza di attrazione inversamente proporzionale al quadrato della distanza esercitata dal Sole, senza considerare l'influenza delle perturbazioni; tuttavia esse (in questo caso causate dal Sole) dovevano necessariamente essere considerate per il moto della Luna intorno alla Terra. Una teoria lunare con una precisione dell'ordine di 2′ d'arco avrebbe fornito un metodo per determinare la longitudine in mare, per il quale la Marina britannica a partire dal 1714 aveva messo in palio una ricca ricompensa. Tuttavia né Euler né altri applicarono il calcolo leibniziano alla determinazione delle perturbazioni prima degli anni Quaranta. La ragione di questo ritardo va ricercata probabilmente nel fatto che le funzioni trigonometriche furono introdotte solamente nel 1739. Fu Euler il primo a scoprire e a spiegare il ruolo di tali funzioni nella risoluzione di equazioni lineari differenziali a coefficienti costanti e sempre a lui si deve la codificazione del calcolo delle funzioni trigonometriche, che rese possibile l'approccio algoritmico al problema delle perturbazioni del moto di un pianeta da parte di un altro.
La spiegazione della precessione degli equinozi e della nutazione
Come abbiamo accennato in precedenza, l'ipotesi di fondo su cui si basava la spiegazione newtoniana della precessione degli equinozi era corretta; il Sole e la Luna, nell'attirare il rigonfiamento equatoriale della Terra, determinano la precessione dell'asse terrestre, cosicché la linea d'intersezione dell'equatore con il piano dell'eclittica ruota in senso orario rispetto al polo settentrionale dell'eclittica. Di conseguenza, l''anno tropico', cioè il periodo di tempo che il Sole, nel suo moto apparente annuo verso est lungo l'eclittica, impiega per ritornare all'equinozio invernale, è più breve dell'anno siderale che costituisce il tempo necessario al Sole per tornare in congiunzione con una stella. Il tentativo di Newton di dare una determinazione quantitativa della precessione, tuttavia, è inficiato da diversi errori. Egli cercò di applicare la dinamica traslazionale in un caso in cui la dinamica richiesta era quella rotazionale; non si trattava, infatti, di un problema di forze e di variazioni di quantità di moto traslazionale, ma di momenti delle forze e di variazioni del momento angolare (la dinamica rotazionale aveva appena cominciato a prendere corpo nell'opera di Huygens e di Johann Bernoulli).
La spiegazione corretta, assieme a un'analisi degli errori di Newton, fu fornita da d'Alembert nell'opera Recherches sur la précession des équinoxes, et sur la nutation de l'axe de la terre, dans le système newtonien, pubblicata nel 1749. Come indica il titolo, d'Alembert si proponeva di spiegare non soltanto la precessione ma anche la nutazione, ossia la piccola oscillazione che si sovrappone al moto di precessione, assai più lento, dell'asse terrestre. La nutazione fu scoperta da James Bradley (1693-1762), professore di astronomia nell'Università di Oxford e astronomo reale, all'inizio degli anni Trenta del Settecento, ma fu annunciata pubblicamente nelle "Philosophical Transactions" soltanto nel gennaio 1748, dopo circa 18 anni di verifiche osservative. Formatosi alla scuola dello zio, l'astronomo dilettante James Pound (m.1724), Bradley era un astronomo osservativo estremamente accurato. La scoperta della nutazione fu un corollario di quella dell'aberrazione della luce, sempre a opera di Bradley, che fu pubblicata sulle "Philosophical Transactions" del gennaio 1729.
Alla fine del XVII sec. gli astronomi, servendosi del micrometro filare, avevano rilevato moti stellari apparenti, senza peraltro riuscire a trovarne una spiegazione convincente. La scoperta dell'aberrazione della luce e della nutazione da parte di Bradley portò ordine nel caos, stabilendo che ogni stella subisce un'oscillazione annuale in longitudine di circa 20″ di ampiezza, che ne altera la posizione nella direzione istantanea del moto di rivoluzione della Terra intorno al Sole; il fenomeno era ricondotto al rapporto finito tra la velocità della Terra e quella della luce, sicché il telescopio doveva essere inclinato in avanti in direzione del moto della Terra affinché la luce della stella entrando nell'obiettivo potesse raggiungere l'oculare. Questa scoperta forniva una significativa conferma sia della finitezza della velocità della luce sia del moto della Terra intorno al Sole.
La nutazione si presenta come un moto supplementare in virtù del quale stelle che si trovino a uguali distanze dallo zenit, su lati opposti del polo celeste, sono soggette a variazioni di declinazione eguali e opposte. Queste variazioni erano dunque attribuibili a un moto oscillatorio dell'asse terrestre. Bradley riteneva che esse fossero dovute alla rotazione in senso retrogrado dei nodi orbitali della Luna, che altera la direzione complessiva dell'attrazione lunare sul rigonfiamento equatoriale della Terra. Poiché una rotazione completa della linea dei nodi lunari impiega 18,6 anni, la nutazione dovrebbe avere un ciclo della medesima durata, ed era questo il ciclo verificato da Bradley allorché finalmente, nel 1748, decise di annunziare la sua scoperta. La notizia stimolò d'Alembert a ricercare una spiegazione adeguata della precessione e della nutazione.
Il trattato di d'Alembert sull'argomento non è certo un modello di chiarezza, ma ciononostante contiene importanti innovazioni. Qui, per la prima volta, sono definite le condizioni complete dell'equilibrio dinamico di un corpo rigido, consistenti nella richiesta che si verifichi l'equilibrio non soltanto delle forze, ma anche dei loro momenti. D'Alembert applicò quest'ultima condizione in accordo con il 'principio di d'Alembert' esposto in precedenza nel Traité de dynamique (1743): un gruppo di corpi interagenti dev'essere considerato come un sistema in equilibrio, nel quale i prodotti massa×accelerazione×braccio, con le accelerazioni invertite rispetto a quelle effettive, vanno considerati alla stregua dei momenti delle forze agenti. D'Alembert fu il primo ad applicare questo principio a un corpo rigido con asse di rotazione mobile. Utilizzando le proprie equazioni differenziali, egli dimostrò che sia la precessione sia la nutazione derivano dall'azione del Sole e della Luna sul rigonfiamento equatoriale.
Dopo aver letto parte della prima sezione del trattato di d'Alembert, Euler si propose di ottenere una propria derivazione; il suo metodo era sostanzialmente identico ‒ sebbene più chiaro ‒ a quello di una seconda derivazione semplificata fornita da d'Alembert, di cui Euler, a quanto sembra, non era a conoscenza. Nel corso degli anni Cinquanta del Settecento Euler procedette alla sistematizzazione della meccanica dei corpi rigidi, formulandola secondo concetti tuttora usati (gli angoli di Euler, i momenti d'inerzia, i momenti angolari).
D'Alembert aveva scritto il suo trattato piuttosto frettolosamente, nel timore di essere preceduto dagli studiosi britannici, nessuno dei quali però, a quanto risultò, si era reso conto degli errori della derivazione newtoniana della precessione, né era ansioso di derivare quantitativamente la nutazione dalla legge di Newton.
Il moto dell'apside lunare e la legge dell'inverso del quadrato
Il calcolo delle perturbazioni
I principali passi del metodo di Clairaut per calcolare le perturbazioni della longitudine di un astro del Sistema solare sono esposti nella Tav. III. Egli lo applicò dapprima alle perturbazioni della Luna e successivamente, alla fine degli anni Cinquanta del Settecento, alle perturbazioni della Terra. Fu questo il metodo che Joseph-Jérôme Le Français de Lalande (1732-1807) scelse di presentare nel suo popolare manuale Astronomie, apparso nel 1764 e, successivamente, nel 1771 e nel 1792.
Nel caso della Luna, Clairaut usò come prima approssimazione per r l'espressione k/[1−ecos(mφ)], dove k, e e m sono costanti, implicando un moto che si svolge su un''ellisse rotante', con la Luna che ritorna all'apogeo dopo aver percorso l'angolo φ=360°/m. Per la costante e Clairaut usò il valore medio 0,05505, dedotto dalle osservazioni, ma stimò k e m identificandoli con espressioni derivate dalla [3] nella Tav. III, in base all'assunto che, a eccezione di termini piccoli, la soluzione prende la forma di un'ellisse rotante. Per m egli ottenne il valore di 0,9958, che implica un moto apsidale di 1°31′ mensili, pari a circa la metà del moto osservato.
Clairaut era conscio del fatto che, al fine di ottenere una teoria più accurata, era necessario effettuare un'approssimazione del secondo ordine, sostituendo nell'espressione di Ω (v. [4] nella Tav. III) il valore di r ottenuto nel primo calcolo e derivando così una nuova espressione più esatta per r. Tuttavia, a suo avviso ciò non avrebbe portato a un'approssimazione significativamente migliore del moto apsidale, in quanto la metà di una quantità non ne costituiva certo una buona stima. Euler era arrivato alla stessa conclusione, che espresse nell'introduzione alla memoria del 1748 premiata dall'Académie Royale des Sciences di Parigi. Sia lui sia Clairaut videro in ciò un motivo per mettere in discussione l'esattezza della legge newtoniana dell'inverso del quadrato. Incoraggiato dalla concordanza di opinioni con Euler, alla metà di novembre Clairaut propose all'Académie di apportarvi una modifica aggiungendo un nuovo termine, proporzionale all'inverso della quarta potenza della distanza.
La proposta fu fortemente osteggiata, in particolare da Georges-Louis Leclerc, conte di Buffon (1707-1788), secondo il quale una legge la cui espressione richiedeva due termini algebrici era ripugnante da un punto di vista filosofico. Al pari di d'Alembert, egli riteneva che la discrepanza scoperta da Clairaut potesse essere spiegata con il magnetismo terrestre. La controversia degenerò in accuse meschine e continuò sino al 1749. Nel frattempo, nel dicembre del 1748, Clairaut scoprì che la seconda approssimazione avrebbe compensato la maggior parte del moto apsidale mancante e depositò una nota di questo tenore presso il segretario perpetuo dell'Académie (l'esecuzione del calcolo dettagliato avrebbe richiesto mesi); la sua teoria completa fu pubblicata infine nel 1752.
Che cosa mise fuori strada Clairaut? Apparentemente egli era partito dall'idea di un'ellisse eccentrica originariamente non perturbata, alla quale le perturbazioni imprimono un moto rotatorio. Lo scostamento dell'orbita lunare da una forma circolare ha però due cause: un'eccentricità originaria e la perturbazione solare, e quest'ultima è forte quanto la prima. L'immagine di un'ellisse in cui il moto rotatorio è impresso da una perturbazione è fuorviante, in quanto il moto apsidale racchiude in sé gli effetti di tutte le diseguaglianze. La scoperta di Clairaut che il moto apsidale poteva essere calcolato correttamente soltanto portando al secondo ordine l'analisi delle forze perturbatrici era di primaria importanza, anche se contraddiceva l'assunto iniziale sul quale si erano basati sia lui sia Euler.
Seguendo l'esempio di Clairaut, Euler prese come prima approssimazione un'ellisse in rotazione e per il moto apsidale trovò un valore che era soltanto la metà di quello osservato. Venendo a sapere del ripensamento di Clairaut, per lungo tempo cercò invano d'individuare l'errore della propria derivazione. Il tema scelto dall'Accademia di Pietroburgo per il suo primo concorso a premio (annunciato nel 1750 per l'anno successivo) fu la teoria lunare ed Euler fu chiamato a presiedere la commissione giudicante. Egli trovò lo scritto di Clairaut di gran lunga migliore delle altre memorie inviate, ma non si ritenne soddisfatto sinché non individuò l'errore nella propria derivazione, radicalmente diversa. Euler aveva assegnato al moto apsidale il suo valore empirico, ma lasciava spazio a una possibile deroga dalla legge dell'inverso del quadrato. Quando alla fine scoprì che a fuorviarlo era stata un'ipotesi frettolosa, e dimostrò che la legge dell'inverso del quadrato era di fatto esatta, il suo apprezzamento per il risultato di Clairaut fu senza riserve.
La teoria lunare di d'Alembert apparve nel 1754. Come prima approssimazione egli postulò un'orbita lunare circolare concentrica alla Terra, di raggio 1/K; nell'equazione differenziale del raggio vettore reciproco u sostituì u con K+u′, dove u′ è una variabile il cui valore resta sempre piccolo rispetto a K. L'equazione differenziale divenne così:
dove N2 è una costante che differisce di poco dall'unità e R è una funzione di u′, du′/dφ e di seni e coseni di multipli di φ. Per risolvere la [3] d'Alembert impiegò un fattore integrante esponenziale, a esponente complesso. Un'approssimazione al primo ordine diede valori del primo ordine per u′ e dunque per du′/dφ, che poterono essere sostituiti in R per ottenere un valore del secondo ordine, e così via. A ogni approssimazione successiva la costante N, che determinava il moto apsidale, fu modificata con l'aggiunta di un nuovo termine. D'Alembert eseguì un numero d'iterazioni sufficiente a ottenere i primi quattro termini del moto dell'apogeo, ossia 1°30′37″, 1°3′21″, 23′30″, 5′5″, per un valore complessivo di 3°2′33″, di appena 1′4″ inferiore a quello osservato. Qui finalmente le ipotesi di partenza non erano errate e le approssimazioni successive erano sviluppate chiaramente.
Tavole solari e lunari con perturbazioni: Lacaille e Mayer
Tra le tavole astronomiche che includevano le perturbazioni, le prime a entrare nell'uso furono le tavole solari di Lacaille, pubblicate nel 1758, e le tavole lunari di Johann Tobias Mayer (1723-1762), che costituirono la base del britannico Nautical almanac, apparso nel 1767. Nella sua storia dell'astronomia del XVIII sec. Jean-Baptiste-Joseph Delambre (1749-1822), professore di astronomia nel Collège de France a Parigi, esaltò Lacaille e Mayer, insieme a Bradley, considerandoli i tre scienziati che nel corso del secolo avevano dato il contributo più decisivo al progresso dell'esattezza della scienza astronomica.
Lacaille fu ammesso all'Académie nel maggio del 1741 per il suo lavoro, svolto in collaborazione con Cassini de Thury, concernente la verifica della misurazione del meridiano da Perpignan a Dunkerque attraverso l'Osservatorio di Parigi (sebbene la relazione sulla missione fosse stata scritta da Lacaille, nel titolo figurava soltanto il nome di Cassini de Thury). Nell'aprile dell'anno successivo Lacaille espose un progetto per costruire un nuovo catalogo stellare, che tenesse conto per la prima volta dei moti apparenti delle stelle identificati da Bradley. Egli invitò gli astronomi dell'Académie a unirsi a lui nella realizzazione del progetto, ma la sua proposta cadde nel vuoto e Lacaille si mise all'opera da solo. Non disponendo di uno 'strumento dei passaggi' (un telescopio orientabile in altezza soltanto sul piano del meridiano locale), calcolò le ascensioni rette delle stelle con il metodo delle 'altezze corrispondenti', registrando i tempi di ascensione e di declinazione di una stella rispetto a due altezze e facendo una media dei due valori per ottenere l'ora del transito al meridiano. Lacaille misurò inoltre l'altezza al passaggio al meridiano e la corresse tenendo conto dell'effetto di parallasse e di rifrazione. In questo modo riuscì a determinare le posizioni delle stelle più luminose dell'emisfero boreale e, nel corso di un soggiorno di due anni al Capo di Buona Speranza, quelle di circa 10.000 stelle dell'emisfero australe. La nuvolosità del cielo di Parigi impedì a Lacaille di completare il catalogo delle stelle boreali.
La compilazione di un catalogo stellare presupponeva una teoria solare riveduta. Attraverso ripetute osservazioni, Lacaille determinò l'eccentricità solare (o terrestre), utilizzando come dati i passaggi al meridiano del Sole (questo metodo, introdotto da Flamsteed, presentava il vantaggio di non dover tenere conto della rifrazione). Con un procedimento analogo Lacaille corresse la posizione della retta apsidale. Utilizzando le osservazioni condotte a Norimberga dal ricco astronomo amatore Bernhard Walther intorno al 1500, egli studiò i mutamenti secolari degli elementi orbitali del Sole, e cercò di verificare e di misurare la perturbazione lunare sul moto solare o terrestre, nonostante le critiche mosse da d'Alembert e da Le Monnier.
Il problema che si poneva era quello di stabilire se il moto della Terra fosse sensibilmente perturbato da pianeti come Giove e Venere. Nel 1750 Euler cominciò a chiedere con sempre maggiore insistenza che l'Académie indicesse un concorso a premio per la risoluzione di tale problema, cosa che avvenne nel 1754 e, in seguito, nel 1756 (anno in cui il premio fu vinto da Euler). Lacaille attese che l'amico Clairaut completasse una deduzione delle perturbazioni e, una volta in possesso di tali dati, intraprese una nuova derivazione degli elementi della teoria solare, tenendo conto delle perturbazioni sia lunari sia planetarie. Le tavole solari di Lacaille, frutto d'innumerevoli notti di veglia e di puntigliosa attenzione per il dettaglio, erano di gran lunga superiori a tutte quelle apparse in precedenza. Se si confrontano le tavole solari di Halley, di Cassini e di Lacaille con le moderne tavole di Simon Newcomb per 22 longitudini osservate del Sole nel periodo compreso tra il 1748 e il 1752, si trovano deviazioni standard dell'ordine di 56,1″ per quelle di Halley, di 32,2″ per quelle di Cassini e di 6,6″ per quelle di Lacaille. La teoria solare fu soggetta a una nuova, significativa revisione soltanto negli anni Ottanta del Settecento, allorché Delambre, seguendo l'esempio di Lacaille e basandosi sul calcolo delle perturbazioni di Lagrange, nonché sulle osservazioni dell'astronomo reale britannico Nevil Maskelyne (1732-1811), rideterminò ex novo gli elementi orbitali.
L'interesse di Mayer per la costruzione di accurate tavole lunari si sviluppò nel corso della sua attività presso l'Ufficio cartografico di Homann a Norimberga. Le eclissi lunari e i fenomeni di occultazione delle stelle erano elementi importanti per determinare le differenze di longitudine terrestre. Le memorie di Mayer sulla librazione e sulle occultazioni lunari, nonché su altri problemi astronomici, gli valsero nel 1750 l'incarico di professore presso l'Accademia Georg-August di Gottinga, con la possibilità di usare i telescopi dell'Osservatorio astronomico della città. Si è affermato che, per le sue tavole lunari, Mayer si basò sulla teoria di Euler, ma si tratta di un errore. In una lettera di Mayer a Euler del 4 luglio 1751 ‒ e quindi precedente alla pubblicazione della 'prima' teoria lunare euleriana del 1753 (la prima in cui le perturbazioni sono derivate esplicitamente) ‒ Mayer dichiarava di aver cercato invano di dedurre le irregolarità lunari dalla teoria newtoniana, sinché non si era imbattuto nella memoria di Euler sulle irregolarità di Giove e di Saturno. Servendosi di questa memoria come modello parziale, Mayer effettuò la propria deduzione indipendente delle perturbazioni lunari; la Theoria lunae, terminata nel 1754 ma pubblicata postuma (1767), contiene 46 termini sinusoidali. Per risparmiare tempo nel calcolo della posizione della Luna, Mayer introdusse 'passi computazionali', quali si ritrovano nella teoria lunare newtoniana, e in tal modo fu in grado di ridurre il calcolo a tredici passi, attraverso i quali la longitudine media della Luna è progressivamente modificata per avvicinarsi a quella reale.
Come dimostravano le osservazioni, le tavole di Mayer nella loro forma finale davano la longitudine della Luna con un'approssimazione massima di circa un minuto d'arco. Gli errori nelle teorie lunari di Clairaut e d'Alembert, e in quella di Euler del 1753, erano tre volte maggiori. La superiore precisione di Mayer era dovuta in larga misura a un accurato adattamento della teoria alle osservazioni. Al pari di Halley, egli utilizzò il ciclo di Saros e con tutta probabilità si servì anche di 'equazioni di condizione', che aveva appreso dalla memoria di Euler del 1749 e aveva efficacemente applicato allo studio della librazione della Luna. Nella Theoria lunae Mayer afferma che molti coefficienti dei termini perturbativi non possono essere derivati dalla teoria se non con grande difficoltà, per questo motivo è opportuno determinarli partendo dalle osservazioni. Anche l'accurata correzione delle posizioni di molte stelle zodiacali contribuì alla riuscita delle tavole di Mayer, che per determinare la posizione della Luna si servì principalmente delle occultazioni di tali stelle da parte del nostro satellite.
Con la speranza di vincere il premio per il metodo di determinazione della longitudine, Mayer inviò le sue tavole alla Marina britannica; tuttavia, a causa della guerra dei Sette anni, la verifica delle tavole in mare fu rimandata. La vedova di Mayer inviò alcune tavole rivedute che furono verificate nel corso di un viaggio alle Barbados nel 1763. All'epoca esse si trovarono a competere con il quarto cronometro di John Harrison, che dava la longitudine con un margine di approssimazione entro 30 miglia nautiche, ossia entro 56 km circa. Per decisione del Parlamento, Harrison ricevette 10.000 sterline, gli eredi di Mayer 3000 sterline, e 300 sterline furono assegnate con sua sorpresa a Euler, in quanto si riteneva erroneamente che fosse stato lui a sviluppare la teoria sulla quale erano basate le tavole di Mayer. Sino agli anni Venti dell'Ottocento le tavole lunari fecero riferimento soprattutto alle osservazioni per la determinazione dei coefficienti dei termini perturbativi.
Il ritorno della cometa di Halley nel 1759
Nel Libro III dei Principia Newton aveva fornito un metodo per adattare elementi parabolici (posizione e data del passaggio al perielio, nodo e inclinazione) a tre osservazioni di una cometa. Gli stessi elementi potevano valere con buona approssimazione anche per un'orbita ellittica anziché parabolica. Il grande astronomo inglese Edmond Halley nell'opera Synopsis astronomiae cometicae (apparsa nel 1705, e ripubblicata nel 1749 in un'edizione ampliata) fornì gli elementi di 24 comete apparse a partire dal XIV secolo. Gli elementi per quelle del 1531, del 1607 e del 1682 erano pressoché identici; le differenze relative al nodo e al perielio tra un'apparizione e l'altra erano al massimo di un grado. Negli intervalli tra le tre apparizioni vi era una differenza di oltre un anno, ma Halley riteneva che ciò potesse essere spiegato con le perturbazioni causate da Giove. Le tre comete, a suo avviso, erano in realtà passaggi diversi di una stessa cometa, la cui ricomparsa poteva essere attesa tra la fine del 1758 e l'inizio del 1759.
Alla metà del 1757, spronato da Lalande, Clairaut si accinse a calcolare la data del passaggio al perielio del ritorno della cometa tenendo conto dell'influenza delle perturbazioni dovute a Giove e a Saturno. La sua idea era quella di calcolare il cambiamento prodotto dalla perturbazione sull'epoca della ricomparsa, relativamente al periodo compreso tra il 1607 e il 1682, e di effettuare poi lo stesso calcolo per il periodo successivo; la differenza, aggiunta all'intervallo 1607-1682, avrebbe dato la lunghezza del periodo che sarebbe iniziato nel 1682. Un calcolo parallelo per i periodi 1531-1607 e 1607-1682 sarebbe servito da verifica del metodo. Gli integrali richiesti potevano essere calcolati per la maggior parte soltanto attraverso metodi numerici; l'eccentricità dell'orbita della cometa, infatti, era talmente grande (secondo le stime di Halley arrivava a 0,96739) che non era possibile utilizzare serie trigonometriche per approssimare gli integrandi. Il metodo di Clairaut consisteva nel calcolare, a intervalli di due gradi di anomalia eccentrica partendo dal perielio, la distanza tra il pianeta perturbatore e la cometa e, successivamente, la forza perturbatrice con le sue componenti radiale e trasversale. I valori successivi dell'integrando potevano poi essere sommati (una formula di correzione fu utilizzata per tenere conto della curvatura della curva in cima alle ordinate). Nelle operazioni di calcolo (la prima integrazione numerica su larga scala che fosse mai stata effettuata), che comportarono circa sei mesi di duro lavoro, Clairaut fu assistito da Lalande e da Nicole Reine Étable de Labrière Lepaute. Nel redigere la relazione finale Clairaut aveva preparato una nota di elogio per l'assistenza di quest'ultima, ma un'amica gelosa insistette perché fosse soppressa. Come ebbe a commentare in seguito Lalande, Clairaut era un "savant judicieux mais faible".
Nella seduta dell'Académie Royale des Sciences del 14 novembre 1758 Clairaut, pur non avendo completato i suoi calcoli, nel timore di essere anticipato dalla cometa espose i risultati preliminari; secondo la sua previsione, il passaggio al perielio sarebbe avvenuto verso la metà dell'aprile dell'anno successivo, con un possibile scarto di un mese. La cometa fu avvistata per la prima volta da Johann Georg Palitzsch in Sassonia il 25 dicembre del 1758, e successivamente a Parigi da Charles Messier, il 21 gennaio del 1759. Il ritorno della cometa divenne universalmente noto dopo il 1° aprile, quando riemerse dai raggi solari dopo il passaggio al perielio; i calcoli dimostrarono che tale passaggio era avvenuto il 13 marzo. D'Alembert e Le Monnier tacciarono d'inesattezza la previsione di Clairaut; in realtà questi aveva mostrato la strada per prevedere con esattezza il ritorno periodico delle comete (anche se la sua previsione aveva in parte tratto vantaggio da una fortunata compensazione di errori) e i successori non avrebbero che emulato e migliorato i suoi stessi metodi.
La parallasse solare e i transiti di Venere del 1761 e del 1769
La parallasse solare orizzontale (propriamente: parallasse diurna orizzontale) è l'angolo φ sotteso dal raggio terrestre r alla distanza d del Sole quando quest'ultimo è all'orizzonte rispetto al generico luogo P (ossia α=90°); da essa si può quindi ricavare la distanza Sole-Terra in termini di misure terrestri. Essa compare nel calcolo della massa terrestre (espressa come una frazione della massa solare), a sua volta necessaria per determinare le perturbazioni provocate dalla Terra su altri pianeti. La massa della Terra varia proporzionalmente al cubo della parallasse solare; di conseguenza, quando Newton nella terza edizione dei Principia assegnò alla parallasse solare un valore di 10,5″ anziché quello più esatto di 8,8″, sovrastimò la massa terrestre di un fattore pari a (10,5/8,8)3 = 1,7.
Tra il 1670 e il 1760 circa, i valori stimati dagli astronomi per la parallasse solare variarono da 9″ a 15″. Halley, a partire dal Catalogus stellarum australium del 1687, sostenne che l'unico metodo per ottenere un valore preciso di questa costante consisteva nell'osservare, da differenti punti della Terra, un transito di Venere sul disco solare. La descrizione più dettagliata di tale metodo apparve nelle "Philosophical Transactions" del 1716. Nel corso di un transito, la distanza di Venere dalla Terra sarebbe di poco superiore a un terzo della sua distanza dal Sole. La distanza angolare tra due traiettorie di Venere sul disco solare osservate da due stazioni terrestri, assieme alla distanza tra queste ultime, consentirebbe la soluzione del triangolo con Venere al vertice e la retta tra le due stazioni come base e darebbe così la distanza Terra-Venere. Il rapporto tra questa distanza e quella Terra-Sole era fissato dalla terza legge di Kepler. I successivi transiti di Venere si sarebbero verificati nel giugno del 1761 e nello stesso mese del 1769. Un ruolo centrale nella preparazione per il transito del 1761 fu assunto da Delisle, il quale si era convinto della sua importanza negli anni Venti del secolo e, mentre era in Russia, tra il 1725 e il 1747, aveva intrattenuto un'estesa corrispondenza con altri astronomi in merito ai problemi tecnici relativi all'impresa. Il suo planisfero, dove erano evidenziati i punti in cui il transito sarebbe stato visibile, e la sua memoria d'istruzioni furono pubblicati dall'Académie Royale des Sciences nel maggio del 1760.
Per l'osservazione del transito del 1761 l'Académie di Parigi inviò osservatori a Vienna, a Pondicherry in India, nell'isola di Rodrigues nell'Oceano Indiano e a Tobol'sk in Siberia. La Royal Society di Londra inviò i propri osservatori a Sant'Elena e a Benkulen nelle Indie Orientali. John Winthrop guidò una spedizione dalla Baia del Massachusetts a Terranova. Altri astronomi si prepararono a osservare il fenomeno in Europa, a Pechino, Calcutta, Madras e Costantinopoli. L'occupazione britannica di Pondicherry impedì all'osservatore dell'Académie di Parigi, Le Gentil, di recarsi sul posto; Charles Mason e Jeremiah Dixon, a seguito di un attacco subito dalla nave che li trasportava da parte di una fregata francese nel Canale della Manica, non riuscirono ad arrivare in tempo nelle Indie Orientali, e osservarono il transito dal Capo di Buona Speranza. A Rodrigues e a Sant'Elena il cielo nuvoloso rese vane le aspettative degli osservatori.
Complessivamente, furono effettuate oltre 120 osservazioni di varia qualità, dalle quali furono ricavati valori della parallasse solare compresi tra 8,28″ e 10,60″. Gli istanti del contatto interno tra l'ombra di Venere e il bordo del Sole erano difficili da calcolare a causa del cosiddetto 'effetto della goccia nera', per cui l'ombra sembra aderire al bordo come una sorta di liquido vischioso. Le longitudini di alcuni dei luoghi di osservazione non erano inoltre note con precisione; sembrava perciò impossibile raggiungere un accordo su un valore medio accettabile. L'interesse si andò spostando sulla preparazione per il transito del 1769 e, dopo la morte di Delisle nel 1768, Lalande si assunse il compito di coordinare gli sforzi internazionali.
Il secondo transito fu osservato da 151 scienziati in 77 stazioni, da Yakutsk alla Baia della California; dall'Endeavour del capitano Cook, Charles Green osservò il transito a Tahiti mentre nelle colonie britanniche del Nordamerica il fenomeno fu osservato da 19 stazioni. L'accademia di Pietroburgo finanziò 13 osservatori, i quali, in generale, erano più preparati e meglio equipaggiati rispetto al transito precedente. La discrepanza tra i risultati calcolati risultò inferiore rispetto al transito precedente, ma ancora assai lontana dall'ordine di precisione di una parte su 500 auspicata da Halley. Le osservazioni considerate più attendibili davano valori compresi tra 8,5″ e 8,9″; in qualche modo fu stabilita una parallasse di circa 8,6″ e l'accordo generale su questo valore durò per ottant'anni. In seguito, i calcoli basati sull'equazione parallattica della Luna e sulle perturbazioni planetarie dovute alla Terra indicarono che 8,6″ era un valore troppo piccolo; i dati desunti dai transiti del 1761 e del 1769 furono di conseguenza sottoposti a una revisione, da cui risultò un valore maggiore. Nel 1895 Simon Newcomb confrontò i contatti di Venere con il bordo del Sole osservati nei transiti del 1761, del 1769, del 1874 e del 1882, arrivando a una parallasse di (8,794±0,023)″. Uno studio della parallasse del pianetino Eros negli anni Trenta del XX sec. restrinse ulteriormente il margine d'imprecisione, anche se in questo caso, come spesso era accaduto in passato, il probabile errore fu sottostimato. A partire dagli anni Cinquanta, le osservazioni con metodi radar dei pianeti hanno aumentato l'accutatezza di parecchi ordini di grandezza; il valore stimato attualmente è di 8,794148″, con un'incertezza di ±7 sull'ultima cifra.
Le equazioni secolari da Euler a Lagrange
Come abbiamo visto, nel saggio del 1748 sulle perturbazioni di Saturno causate da Giove, premiato dall'Académie Royale des Sciences, Euler si rese conto che nella sua analisi emergevano arcs de cercle ‒ ossia termini che aumentavano in proporzione al tempo ‒ a meno di non considerare le perturbazioni di Giove e di Saturno simultaneamente. In una memoria del 1752, che risultò vincitrice del premio messo in palio dall'Académie, egli cercò di analizzare l'interazione dei due pianeti in rapporto all'influsso reciproco esercitato sulle rispettive eccentricità orbitali. Scoprì così che l'eccentricità orbitale di ciascun pianeta produce un'eccentricità orbitale nell'altro; ogni pianeta ha un'eccentricità propria e una accidentale, che influenza il suo raggio vettore e la sua longitudine nel moto rispetto all'afelio dell'altro pianeta. L'eccentricità osservata sarebbe la risultante di queste due eccentricità e muta nel tempo a causa del variare delle distanze angolari tra i due afeli. Si trattava di una conclusione esatta dal punto di vista qualitativo, ma le determinazioni quantitative di Euler, che indicavano un'accelerazione nei moti medi di entrambi i pianeti, erano inficiate da alcuni errori di calcolo. Lo scritto in questione fu pubblicato nella raccolta delle memorie premiate dalla Académie. Nel 1765 lo stesso problema era stato affrontato da un matematico di ventinove anni, Joseph-Louis Lagrange (1736-1813), che aveva in precedenza comunicato a Euler l'invenzione del suo calcolo delle variazioni e nel 1764 aveva scritto una memoria sulla librazione della Luna, che fu premiata dall'Académie di Parigi. Un'altra memoria sulle perturbazioni dei satelliti di Giove gli valse il premio per il 1766. Nello stesso anno, allorché Euler fece ritorno a Pietroburgo, Lagrange fu nominato suo successore all'Accademia di Berlino, dove rimase per 21 anni, per poi passare all'Académie nel 1787.
Nella prima parte della memoria sulle perturbazioni dei quattro satelliti galileiani di Giove, Lagrange dà una soluzione del primo ordine delle equazioni di moto (il raggio vettore nell'espressione delle forze perturbatrici è assunto come costante), e fornisce una derivazione delle principali anomalie dei satelliti. Queste erano state determinate per via osservativa dall'astronomo svedese Pehr Wilhelm Wargentin (1717-1783). I moti medi dei primi dei tre satelliti stanno l'un l'altro all'incirca nella proporzione di 4:2:1; questa quasi commensurabilità porta, nelle integrazioni, a piccoli divisori nei coefficienti di alcuni termini perturbativi, facendoli dunque aumentare sino a renderli rilevabili. Per Lagrange questa quasi commensurabilità restava un fenomeno inspiegabile, ma importante.
Nella seconda parte della memoria è spiegata la ragione della comparsa degli arcs de cercle nel processo iterativo standard per le perturbazioni; si tratta di un segno del lento processo di variazione subito dagli elementi orbitali. Nella memoria del 1752 Lagrange effettuò con successo i calcoli che Euler aveva condotto in modo approssimativo. L'eccentricità orbitale di ciascun satellite sarebbe la risultante di un'eccentricità originaria e di percepibili eccentricità avventizie, causate da quelle orbitali degli altri tre satelliti ‒ una situazione che si rispecchia con esattezza nelle inclinazioni orbitali. Gli apocentri (o apofuochi, i punti di un'orbita ellittica maggiormente distanti dal fuoco principale) delle numerose orbite progrediscono, i nodi regrediscono, le eccentricità e le inclinazioni subiscono oscillazioni periodiche.
Mentre portava a termine questa memoria, Lagrange intraprese un'analisi delle interazioni tra Giove e Saturno basata sugli stessi criteri, derivando le variazioni secolari delle eccentricità, degli afeli, delle inclinazioni e dei nodi che ognuno dei due pianeti causa nell'altro (per 'variazione secolare' s'intende qui una variazione di lungo periodo indipendente dalla configurazione momentanea dei pianeti). Nei 'moti medi' Lagrange trovò termini proporzionali ai quadrati del tempo: un'accelerazione di Giove pari a +(2,7402N2)″, dove N è il numero di rivoluzioni dall'inizio del periodo considerato, e una decelerazione di Saturno pari a −(14,2218N2)″.
Le osservazioni confermavano sul piano qualitativo tale risultato; in Giove, infatti, si riscontrava un'accelerazione, in Saturno una decelerazione. I risultati di Lagrange, pubblicati nel III volume della Miscellanea Taurinensia (1763-1765), sarebbero stati messi in discussione da Laplace per quanto riguarda i moti medi.
La rivalità tra Laplace e Lagrange
Pierre-Simon de Laplace lasciò la Bassa Normandia per trasferirsi a Parigi all'età di 19 anni, munito di una lettera di presentazione di d'Alembert il quale, resosi ben presto conto del talento matematico del giovane, gli procurò un posto di professore di matematica presso l'École Militaire. Nel 1770 Laplace presentò la prima delle numerose memorie che avrebbe inviato all'Académie Royale des Sciences nel corso dei successivi 53 anni. Tra queste, la prima a essere pubblicata apparve nel 1776 nei "Savants étrangers" dell'Académie per il 1773, con il titolo Sur le principe de la gravitation universelle et sur les inégalités séculaires des planètes qui en dépendent. Laplace divenne membro associato dell'Académie nel 1773, poi membro a pieno titolo, e quindi con diritto a una pensione nel 1785.
La sorprendente conclusione della memoria di Laplace sulle perturbazioni secolari era che i moti medi dei pianeti non risentivano della variazione secolare. Colpito dalla discrepanza tra i valori delle variazioni secolari di Giove e di Saturno fornite da Euler e da Lagrange, Laplace decise di sviluppare una propria derivazione. In primo luogo, Laplace eliminò nelle equazioni differenziali del vettore r e della longitudine φ tutti i termini che contenevano la massa del pianeta perturbatore (δm′) e integrò le equazioni. Dopodiché, δ-differenziò le equazioni risultanti dall'integrazione e introdusse nuovamente i termini contenenti δm′. Utilizzando la commutabilità di δ con l'operatore differenziale standard 'd', Laplace ottenne equazioni differenziali per δr e δφ, variazioni di r e φ causate da δm′, e le risolse con il metodo dei coefficienti indeterminati. L'espressione dell'accelerazione del moto medio era proporzionale a un fattore dipendente dai coefficienti che comparivano nelle serie trigonometriche di v‒3, l'inverso del cubo della distanza tra il pianeta perturbatore e quello perturbato. Laplace sviluppò l'espansione di v‒3, più di quanto non avessero fatto Euler e Lagrange, giungendo sino all'ordine dell'eccentricità elevata al cubo. Utilizzando la riduzione, sviluppata da Euler, dei coefficienti successivi a espressioni nei termini dei primi due, egli dimostrò che il fattore era sempre zero. Così, al primo ordine in δm′ e al quarto ordine nell'espansione di v‒3, l'accelerazione del moto medio si dimostrava nulla. Egli arrivò così a concludere che l'apparente accelerazione secolare di Giove e l'apparente decelerazione secolare di Saturno non potevano essere dovute alla gravitazione reciproca. La causa, egli suggerì, avrebbe potuto essere l'attrazione esercitata dalle comete.
Nel 1774 Lagrange inviò all'Académie una memoria in cui presentava un nuovo metodo per determinare le variazioni secolari dei nodi e delle inclinazioni dei pianeti. Il passo cruciale del metodo consisteva nel sostituire le variabili impiegate sino ad allora, ossia la tangente all'eclittica dell'inclinazione orbitale (indicata con θ) e la longitudine del nodo ascendente (indicata con ω) con due nuove variabili, s=θsenω e u=θcosω. Se nelle equazioni differenziali di s e u i raggi vettori sono assunti costanti (e dunque si assumono orbite circolari) e si scartano termini dipendenti dalle posizioni dei pianeti, le equazioni diventano lineari e hanno soluzioni 'oscillanti'. Giove e Saturno, date le loro masse straordinariamente grandi, potevano essere trattati come un sistema a sé stante; Lagrange trovò che i nodi di questi pianeti subiscono oscillazioni opposte con un periodo di 51.150 anni, e lo stesso vale per le loro inclinazioni orbitali.
Questa memoria fu pubblicata solamente nel 1778, ma Laplace ebbe occasione di prenderne visione al suo arrivo a Parigi, e intuì che un metodo del tutto analogo poteva essere applicato alle eccentricità orbitali (e) e agli afeli (A) dei pianeti, se queste variabili fossero state sostituite rispettivamente dalle variabili x=esenA e y=ecosA. Anche Lagrange aveva intuito quest'analisi parallela, ma fu Laplace a pubblicarla per primo, nella memoria inviata all'Académie nel 1772, che apparve nel 1775. In una seconda memoria egli dimostrò che gli arcs de cercle, che emergevano quando le equazioni differenziali del moto planetario erano risolte per approssimazioni successive, potevano essere eliminati tenendo conto delle variazioni secolari delle nuove variabili. A conclusione di questa memoria Laplace esprimeva il proposito di applicare la nuova teoria a tutti i pianeti.
In una lettera a Laplace del 10 aprile 1775, Lagrange (cui Laplace aveva inviato una copia di queste memorie prima della pubblicazione) offrì di lasciare la trattazione dell'intero problema delle perturbazioni planetarie al giovane rivale. Sei mesi dopo, in una lettera a d'Alembert, ritirò l'offerta proponendo invece che lui e Laplace s'impegnassero in una gara amichevole, scambiandosi soltanto le memorie pubblicate sulle perturbazioni planetarie; alcuni anni dopo Lagrange osserverà in una lettera a Laplace: "Io non sono invidioso a causa del mio carattere; voi non lo siete a causa del vostro successo" (Lagrange a Laplace, 30 dicembre 1776, Serret 1892, p. 71). Utilizzando il proprio metodo di variazione dei parametri orbitali, Lagrange si accinse a derivare sistematicamente le variazioni secolari e periodiche dei sei pianeti conosciuti (delle variazioni periodiche derivò soltanto i termini indipendenti dalle eccentricità). I trattati che contengono queste derivazioni apparvero nei "Mémoires" di Berlino dal 1783 al 1785. Laplace, per contro, ignorando i valori esatti delle masse di Mercurio, Venere e Marte, nonché l'incidenza delle perturbazioni planetarie causate dalle comete, non ritornò sul tema sino alla fine del 1785.
Nel frattempo, Lagrange introdusse un'innovazione destinata a segnare un radicale mutamento nella teoria delle perturbazioni: l'uso di una funzione potenziale dalla quale era possibile ricavare le forze agenti su un pianeta, nella direzione individuata da una certa coordinata, effettuando una derivazione parziale rispetto a quest'ultima. Lagrange aveva utilizzato per la prima volta questa funzione in una memoria dedicata all'effetto sul moto lunare di distribuzioni di massa non sferiche nella Terra o nella Luna; questa memoria vinse il premio dell'Académie nel 1774. L'applicazione della stessa idea a un sistema di masse puntiformi fu effettuata in due memorie presentate all'Accademia di Berlino nell'ottobre del 1776 e nello stesso mese dell'anno successivo, pubblicate entrambe nel 1779. In esse Lagrange usò il simbolo Ω per la funzione potenziale ‒ forse un tacito tributo a Clairaut il quale aveva usato il simbolo Ω per racchiudere in esso tutti gli effetti perturbativi. La prima memoria forniva una nuova dimostrazione, più generale di quella di Laplace, dell'immunità dei moti medi dalla variazione secolare; essa assumeva che nessuna combinazione lineare dei moti medi di tutti i pianeti può essere uguale a zero. Era veramente così? Sia Lagrange sia Laplace erano convinti che tale ipotesi fosse corretta. "L'eleganza e la semplicità della vostra analisi‒ scriveva Laplace ‒ mi hanno procurato un piacere indicibile" (Laplace a Lagrange, 9 giugno 1779, ibidem, pp. 83-84).
La seconda applicazione costituiva una derivazione degli integrali del moto per un sistema di corpi interagenti conformemente alla legge gravitazionale dell'inverso del quadrato della distanza. Prendendo il baricentro del sistema come origine delle coordinate, Lagrange ridusse l'espressione della funzione potenziale a una serie di termini, ognuno dei quali ha un prodotto di due masse al numeratore e la distanza tra esse al denominatore. Con agilità ed eleganza Lagrange riuscì a dimostrare poi che il baricentro del sistema si muove uniformemente e che il momento angolare e la force vive totale si conservano.
A partire dai primi anni Ottanta del Settecento Laplace utilizzò la funzione potenziale nel suo lavoro sull'attrazione di sferoidi. Quando, verso il 1785, ritornò sul problema delle perturbazioni in un sistema di masse puntiformi che si attraggono, fece della funzione potenziale, che chiamò 'funzione perturbatrice', il punto di partenza della sua analisi. L'introduzione di questa funzione, che semplificava i calcoli e presentava i risultati in una forma facilmente comprensibile, costituiva secondo Laplace un'autentica scoperta. Lagrange preparò, inoltre, la strada alla ripresa del problema delle perturbazioni planetarie da parte di Laplace (Tav. IV).
È probabile che Laplace leggesse questa memoria a pochissima distanza dalla pubblicazione, nel 1785, così come si premurava di leggere tutto ciò che scriveva Lagrange. Il primo dei suoi grandi trionfi del 1785-1787 sarebbe derivato da un'applicazione del suggerimento con il quale quella memoria si concludeva, ma non a dΣ, bensì a dp.
La spiegazione di Laplace delle principali anomalie
In una memoria presentata all'Académie Royale des Sciences il 3 novembre del 1785, Laplace spiegò in quale modo si poteva risolvere la grande anomalia nei moti di Giove e di Saturno che aveva suscitato le perplessità degli astronomi a partire da Flamsteed. Le perturbazioni periodiche che ciascuno di questi due pianeti ‒ ma il discorso vale in generale per pianeti qualsiasi ‒ causa nel moto medio dell'altro possono essere espresse da termini della forma Ksen(i1n1+i2n2)t, dove n1 e n2 sono i moti medi rispettivamente del pianeta perturbatore e di quello perturbato, per esempio in gradi ad anno, i1 e i2 sono numeri interi arbitrari positivi o negativi, e t è il tempo espresso in anni. Il coefficiente K della maggior parte di questi termini sarà estremamente piccolo, sicché essi risultano impercettibili all'osservazione. Laplace esaminò i fattori che entrano in K. Essi comprendevano un prodotto di eccentricità e tangenti dell'inclinazione di ordine (i1+i2); sia le eccentricità sia le tangenti dell'inclinazione sono minori di 1, e di conseguenza quanto maggiore sarà l'ordine (i1+i2), tanto minore risulterà K; per questa ragione Euler e Lagrange avevano in precedenza ignorato i termini di ordine superiore. K contiene però anche il fattore n22/(i1n1+i2n2)2, che emerge da una doppia integrazione; se n1 e n2 sono quasi commensurabili e i1 e i2 sono di segno opposto, questo fattore può essere molto grande, come aveva messo in evidenza Lagrange.
Consideriamo il termine che descrive la perturbazione esercitata da Giove su Saturno in cui i2=5 e i1=−2; il moto medio di Saturno è di circa 360°/29,46 anni e quello di Giove di circa 360°/11,86 anni, sicché il valore della frazione n22/(5n2−2n1)2 è pari a circa 974; il periodo di questa irregolarità ‒ il tempo t necessario affinché (5n2−2n1)t sia eguale a 360° ‒ è di circa 900 anni. Inoltre, i2+i1=5−2=3; di conseguenza, K ha tra i suoi fattori una somma di potenze e prodotti delle eccentricità e delle tangenti delle inclinazioni di terzo ordine, che riduce la grandezza di K; i due fattori si compensano parzialmente, e il risultato totale è un termine dipendente dalla longitudine di Saturno esprimibile con −49′sen(5n2−2n1+k2)t, dove k2 è una costante. Il termine corrispondente per Giove è invece esprimibile come 20′sen(5n2−2n1+k1)t. Queste sono le più grandi perturbazioni esistenti nel Sistema solare; prima della loro scoperta, i moti di Giove e di Saturno rappresentavano un mistero e la validità della teoria newtoniana per la spiegazione dei moti planetari restava incerta. Laplace risolse questo mistero ed eliminò ogni dubbio. Alcune indicazioni empiriche avrebbero potuto portare a scoprire ancora prima la 'grande irregolarità'; tale scoperta rappresentò invece il frutto di uno sviluppo strettamente interno degli algoritmi della teoria delle perturbazioni.
Nella stessa memoria in cui annunciò la soluzione dell'anomalia dei moti di Giove e di Saturno, Laplace fornì anche una spiegazione delle curiose simmetrie nei moti dei primi tre satelliti galileiani di Giove. Il moto medio, n, del primo è di poco superiore al doppio del moto medio, n′, del secondo, e n′ a sua volta è poco più del doppio di n″, il moto medio del terzo satellite; la relazione (n−n′)=2(n′−n″) appare esatta, cosicché n+2n″=3n′. Inoltre, indicando con λ, λ′ e λ″ le longitudini dei tre satelliti in un dato tempo, risulta λ−3λ′+2λ″=180°. Nella memoria sui satelliti di Giove, premiata nel 1766, Lagrange aveva menzionato queste relazioni senza darne una spiegazione. Laplace portò l'analisi perturbativa delle interazioni di questi satelliti al secondo ordine nelle masse e dimostrò che s=n−3n′+2n″ e V=λ−3λ′+2λ″ erano quantità periodiche che variano tra 0° e 180°. Ne conseguiva che i satelliti non dovevano essere necessariamente collocati all'origine, esattamente nelle posizioni e nelle distanze giuste da Giove, affinché le relazioni s=0° e V=180° fossero valide; se posti anche soltanto approssimativamente in tali posizioni, le loro interazioni gravitazionali avrebbero fatto il resto, indirizzandoli verso una relazione stabile tra i loro moti. è noto che tali stabilità persistono nonostante l'azione delle forze di marea esercitate da Giove sui suoi satelliti, che determinano un lento aumento delle loro distanze dal pianeta.
L'ultima grande anomalia del Sistema solare non ancora spiegata nel 1785 era costituita dall'accelerazione secolare apparente della Luna, che Halley aveva scoperto nel 1693. Nel 1749, confrontando le eclissi dell'Antichità e quelle moderne, Richard Dunthorne scoprì l'esistenza di un incremento di 10″ nel moto medio in un dato secolo (in due secoli tale incremento ammonterebbe a 40″). Johann Tobias Mayer nelle sue ultime tavole lunari stimava l'incremento in un secolo pari a 9″. Per la risoluzione di questo problema l'Académie di Parigi indisse tre concorsi, nel 1770, nel 1772 e nel 1774, ma non emerse alcuna causa gravitazionale alla quale imputare il fenomeno. Euler lo attribuiva alla resistenza di un etere; altri formularono l'ipotesi che la rotazione diurna della Terra subisse un progressivo rallentamento, dovuto forse all'azione dei venti costanti di ponente. Lo stesso Laplace aveva suggerito nel 1773 che il fenomeno potesse essere causato da una velocità finita di propagazione della forza gravitazionale. Dopo aver portato a termine la Théorie de Jupiter et de Saturne nell'agosto del 1786, Euler riesaminò la questione e individuò alla fine una possibile causa indiretta del fenomeno nell'oscillazione secolare dell'eccentricità dell'orbita terrestre, da lui scoperta insieme a Lagrange negli anni Settanta. Il 19 dicembre del 1787 tale teoria fu presentata all'Académie. Un effetto netto dell'azione perturbatrice del Sole sulla Luna è quello di far diminuire la forza d'attrazione della Terra su quest'ultima; di conseguenza, la Luna si muove in un'orbita leggermente più ampia di quella che seguirebbe altrimenti, e il suo moto angolare intorno alla Terra è più lento. Si tratta peraltro di un effetto variabile, che dipende dall'eccentricità orbitale della Terra, attualmente in diminuzione; Laplace dimostrò che tale diminuzione comporta un decremento della componente radiale verso l'esterno della forza perturbatrice del Sole, portando a un incremento di 11″ nel moto medio della Luna nel corso di un secolo. Le eclissi del passato sembravano confermare pienamente questo risultato teorico.
I fenomeni che apparivano inspiegabili sulla base della legge gravitazionale, concludeva Laplace, erano così ricondotti a tale legge, di cui fornivano una nuova, significativa conferma. "Allora il sistema dell'Universo oscilla soltanto intorno a uno stato medio, da cui non si discosta mai se non di pochissimo. In virtù della sua costituzione e della legge di gravitazione, esso gode di una stabilità che non può essere annullata se non da cause esterne [...]" (Sur l'équation séculaire de la lune, in Oeuvres, XI, p. 249).
Nel 1853 John Couch Adams (1819-1892), astronomo a Cambridge in Massachusetts, dimostrò che il calcolo laplaciano dell'accelerazione secolare della Luna era soltanto parzialmente corretto, in quanto non teneva conto della componente tangenziale della forza perturbatrice del Sole, che riduce l'effetto totale, sicché l'incremento calcolato dovrebbe essere di 6″ in un secolo. Tuttavia, l'effetto osservato restava di 11″ in un secolo. Nella seconda metà dell'Ottocento si fece strada la convinzione che questa differenza di 5″ fosse dovuta a una decelerazione della rotazione terrestre causata dall'attrito delle acque durante il fenomeno delle maree; ma il fenomeno, in realtà, è assai più complesso. Nel 1920 John Knight Fotheringham, studiando le eclissi dell'Antichità trovò che l'incremento del moto medio della Luna a secolo ammontava a 10,8″ e quello del Sole a 1,5″. Quest'ultimo effetto è causato semplicemente dal ritardo nella rotazione terrestre, che produce anche un'accelerazione apparente della Luna 13,4 volte maggiore (13,4 essendo il rapporto tra il moto medio della Luna e quello del Sole) ‒ ossia un incremento apparente nel moto medio di 20″ a secolo. Sommando i 6″ trovati da Adams, si ottiene un incremento atteso di 26″, maggiore di 15″ rispetto a quello osservato. La spiegazione più plausibile di questa discrepanza è che la Luna trae energia dalle sue interazioni di marea con la Terra, e che dunque ascende a un'orbita più ampia laddove il suo moto angolare medio è minore.
L'Exposition du système du monde e la Mécanique céleste
Per quanto riguarda il problema della stabilità del Sistema solare, le formulazioni attuali hanno contorni accuratamente delineati. Per Sistemi solari con pianeti sufficientemente piccoli, le condizioni iniziali implicano nella maggior parte dei casi orbite stabili; le orbite instabili si discostano dalla stabilità lentamente rispetto al ciclo di vita di una stella come il Sole. Laplace non era a conoscenza di restrizioni di questo genere; il suo Sistema solare, a meno d'interventi esterni, era stabile senza condizioni. A sua discolpa bisogna dire che le evidenze che aveva a disposizione erano piuttosto frammentarie e contraddittorie, ma la sua ambizione è peraltro innegabile; le sue scoperte dovevano tradursi in un vero e proprio trionfo.
Alla Rivoluzione subentrò il Terrore e molti colleghi di Laplace ‒ tra i quali Lavoisier, Bailly, Bochart de Saron ‒ finirono sulla ghigliottina. Espulso con un decreto del dicembre 1793 dalla Commissione per i pesi e per le misure perché sospettato di non possedere a sufficienza "virtù repubblicane e odio nei confronti della monarchia", Laplace si rifugiò a Melun, dove mise mano al suo capolavoro.
La sua Exposition du système du monde, la cui prima edizione risale al 1796, è una spiegazione semidivulgativa del Sistema solare, formulata in una prosa elegante e senza nemmeno una formula. In una nota al termine dell'opera Laplace introdusse la cosiddetta 'ipotesi della nebulosa', secondo la quale il Sole sarebbe stato originariamente una massa rotante incandescente dalla quale, nel corso del suo raffreddamento, si sarebbero condensati successivamente i pianeti. L'ipotesi spiegava perché i pianeti e i satelliti si muovono quasi tutti sullo stesso piano (l'eclittica), nella stessa direzione, seguendo orbite quasi circolari, con rotazioni assiali in senso orario rispetto al Polo Nord dell'eclittica (l'ipotesi cosmologica formulata in precedenza da Buffon, secondo la quale i pianeti si sarebbero distaccati dal Sole a seguito del passaggio di una cometa, implicava orbite più strette ed eccentriche). L'ipotesi della nebulosa primordiale è diventata ormai un punto di riferimento nel dibattito contemporaneo sull'origine del Sistema solare.
Il Traité de mécanique céleste di Laplace (i primi quattro volumi apparvero tra il 1798 e il 1805; il quinto e ultimo fu pubblicato nel 1825) forniva invece una spiegazione fortemente matematizzata della struttura del Sistema solare. L'espressione "meccanica celeste" da lui coniata in analogia con la Méchanique analitique (1788) di Lagrange, finì per rimpiazzare la locuzione 'astronomia fisica' usata in precedenza. Nella Méchanique analitique Lagrange aveva trattato la meccanica come una scienza puramente matematica; la Mécanique céleste di Laplace, che associava alla formulazione teorica una dettagliata trattazione delle applicazioni, divenne la guida principale e il più fecondo stimolo per gli astronomi del XIX secolo.
La maturità dell'astronomia
Nel 1833 il grande naturalista e filosofo inglese William Whewell (1794-1866) proclamò l'astronomia "la regina delle scienze, […] esempio di una scienza in quello stadio elevato di piena maturità in cui non resta altro da fare se non determinare con la massima precisione le conseguenze delle sue leggi attraverso le più sofisticate combinazioni di tecniche matematiche, e ottenere la mole dei suoi dati attraverso l'osservazione più attenta e scrupolosa" (Report of the third meeting of the British Association for the advancement of science, p. XIII).
Alla base di questo duplice sviluppo dell'astronomia, matematico e osservativo, vi furono nel Settecento tradizioni alquanto diverse. I cinque matematici ai quali, come abbiamo visto, si devono principalmente gli sviluppi analitici dalla legge gravitazionale di Newton, potevano contare su uno stipendio corrisposto da istituzioni finanziate dal governo, come le accademie delle scienze di Berlino, Parigi e Pietroburgo; le loro opere apparvero quasi esclusivamente nelle memorie ufficiali di queste, e alcune delle più importanti furono scritte per i concorsi indetti dalle accademie che offrivano ricchi premi in denaro. Gli sviluppi della matematica avvennero nell'ambito della tradizione algoritmica fondata da Leibniz e da Johann I Bernoulli e furono al tempo stesso formali e approssimativi.
Nel corso del XVIII sec. gli osservatori astronomici si moltiplicarono; le osservazioni più utilizzate dai teorici furono quelle relative ai transiti degli astri effettuate dagli astronomi reali britannici James Bradley e Nevil Maskelyne; le osservazioni di Bradley furono pubblicate tra il 1798 e il 1805, dopo una lunga battaglia legale tra i suoi eredi e la Marina britannica; quelle di Maskelyne furono le prime a essere pubblicate regolarmente a spese del governo. Nel corso del Settecento gli strumenti ottici più apprezzati furono quelli realizzati da costruttori britannici: Graham, Bird, Short, Sisson, Dollond, Ramsden. Il fatto che l'Osservatorio di Parigi non fosse riuscito a istituire un programma sistematico di osservazioni fu attribuito da Delambre all'influenza dominante di Cassini sino alla Rivoluzione e dopo il 1795 a quella di Laplace, il quale subordinava tutto al suo progetto di 'coprire a tappeto' l'astronomia planetaria. Non fu creato alcun catalogo stellare; "mai", ammoniva Delambre, "mettere un matematico a capo di un osservatorio".
La pubblicazione nel 1792 della terza edizione della Astronomie di Lalande, con le nuove tavole di Giove, di Saturno e dei satelliti di Giove costruite da Delambre sulla base delle teorie di Laplace, e la pubblicazione dei primi due volumi della Mécanique céleste, nel 1798 e nel 1799, stimolarono gli astronomi a impegnarsi in una gara nel tentativo di fornire osservazioni caratterizzate dallo stesso grado di accuratezza raggiunto nella costruzione teorica. Il centro dell'innovazione nel campo dell'osservazione astronomica si spostò in Germania. Se alla fine del XVIII sec. l'accuratezza con cui erano registrate le osservazioni era arrivata a 1″, un limite oltre il quale ‒ riteneva Jean-Sylvain Bailly nel 1772 ‒ sarebbe stato impossibile spingersi, nel secolo successivo questo limite sarebbe stato ulteriormente ridotto, sino a giungere a 0,01″.