iperbole
iperbole
iperbole curva piana aperta, ottenuta come luogo dei punti P del piano tali che la differenza delle loro distanze da due punti fissi, F1 e F2, detti fuochi, risulti costante in valore assoluto. È costituita da due rami, con due distinti punti reali all’infinito, che rappresentano le direzioni dei suoi asintoti. Si ottiene anche come sezione di un cono circolare indefinito con un piano che forma con l’asse del cono un angolo minore dell’apertura del cono stesso: è pertanto, con l’→ ellisse e la → parabola, una → conica. Un’iperbole può essere definita anche come luogo dei punti del piano le cui distanze da un punto fisso (fuoco) e da una retta fissa (direttrice) sono in rapporto costante e > 1. Tale rapporto costante è detto eccentricità dell’iperbole.
Elementi caratteristici di un’iperbole sono, oltre ai fuochi F1 e F2:
• l’asse principale: la retta passante per i fuochi (detto anche asse trasverso);
• l’asse secondario: l’asse del segmento F1F2 (detto anche asse non trasverso);
• il centro: il punto di intersezione dei due assi;
• i vertici: i due punti in cui l’asse principale interseca la curva;
• gli asintoti: le rette passanti per il centro e tangenti alla curva all’infinito;
• i diametri: i segmenti intercettati dall’iperbole su una retta che passa per il suo centro.
In coordinate cartesiane ortogonali non omogenee l’equazione di un’iperbole è
con
L’iperbole è quindi una curva algebrica del secondo ordine. In un riferimento che ha per origine il centro dell’iperbole e per asse delle ascisse l’asse principale, cioè la retta per i due fuochi F(c, 0) e F′ (−c, 0) (con c > 0) e per differenza delle distanze del generico punto P dai due fuochi la costante 2a < 2c, l’equazione cartesiana dell’iperbole assume la forma più semplice
avendo posto c2 = a2 + b2.
Se invece il riferimento è scelto in modo che l’asse secondario sia l’asse delle ascisse, l’equazione dell’iperbole assume la forma
L’equazione
è detta forma canonica e, a seconda che si consideri il segno + o il segno −, rappresenta un’iperbole con i fuochi sull’asse delle ascisse o sull’asse delle ordinate, i cui asintoti sono le rette di equazioni
Se nell’equazione canonica risulta a = b, gli asintoti risultano perpendicolari fra loro: in tale caso l’iperbole si dice equilatera. In ogni iperbole equilatera, il triangolo rettangolo individuato dagli asintoti e dalla tangente all’iperbole in un suo punto P ha area costante, al variare di P sulla curva. Assumendo come assi cartesiani due rette parallele agli asintoti di un’iperbole equilatera, la sua equazione assume la forma
in tal caso gli asintoti hanno equazione
Se in particolare gli assi del sistema di riferimento sono paralleli e coincidenti con gli asintoti, l’equazione assume la forma xy − k = 0, equivalente a
ed esprime la legge di proporzionalità inversa (→ proporzionalità).
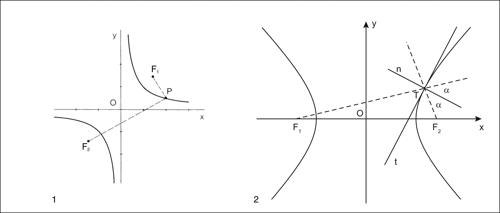
Una retta generica interseca un’iperbole in non più di due punti reali. Se la retta non ha punti in commune con la curva è detta retta esterna all’iperbole, se ha in comune due punti distinti o un solo punto è detta retta secante all’iperbole, se ha in commune due punti coincidenti la retta è tangente all’iperbole. Da un punto P del piano si possono condurre al massimo due distinte tangenti a una iperbole. Se il punto P è nella regione di piano individuata dall’iperbole e non contenente i fuochi, per P passano due tangenti reali e distinte, se P è in una delle due regioni contenenti uno dei fuochi, per P non è possibile tracciare alcuna tangente reale. Se, infine, P appartiene all’iperbole la tangente è una sola. L’iperbole gode di una importante proprietà detta proprietà focale dell’iperbole: le rette n e t, rispettivamente normale e tangente all’iperbole in un suo punto T, sono le bisettrici delle rette passanti per T e per i fuochi.