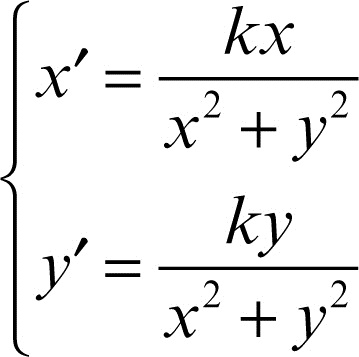inversione circolare

inversione circolare

inversione circolare in geometria, corrispondenza del piano in sé stesso tale che, fissati un punto O del piano (centro di inversione) e una costante k > 0 (costante di inversione), associa a ogni punto P del piano, eccettuato O, il punto P′ appartenente alla semiretta con origine in O e passante per P tale che il prodotto delle lunghezze dei due segmenti OP e OP′ sia uguale a k. Il cerchio di centro O e raggio √(k) è detto cerchio di inversione: la locuzione è giustificata dal fatto che con tale corrispondenza a ogni punto interno a tale cerchio, eccettuato O stesso, corrisponde un punto esterno, e viceversa, mentre i punti della circonferenza rimangono fissi. In un riferimento cartesiano ortogonale, con origine nel punto O, l’inversione circolare di centro O e costante k è espressa dalle equazioni

Un’inversione circolare centrata in O è involutoria, nel senso che applicata due volte dà l’identità. Valgono inoltre le seguenti proprietà:

• a una retta per O corrisponde la retta stessa;

• a una retta non passante per O corrisponde una circonferenza per O la cui tangente in O è parallela alla retta data;

• a una circonferenza non passante per O corrisponde una circonferenza non passante per O.

Questa trasformazione si può costruire direttamente nel piano con uno strumento costituito da due rombi articolati (uno interno all’altro) aventi in comune due vertici opposti. Si impernia al piano uno dei vertici del rombo con i lati maggiori (diventa così un punto fisso nella trasformazione e ne costituisce il centro) e si ottiene una inversione circolare nella quale si corrispondono i punti (allineati col centro) che sono vertici opposti del rombo con i lati minori. Se invece si assume come centro della trasformazione (imperniandolo al piano) uno dei vertici del rombo che ha i lati minori si ottiene una antinversione circolare (circonferenza base con raggio immaginario) nella quale si corrispondono i punti (allineati col centro) che sono vertici del rombo con i lati maggiori.

L’inversione circolare può essere estesa allo spazio tridimensionale in relazione a una sfera (sfera d’inversione), il cui centro è il centro di inversione. Va osservato inoltre che l’inversione circolare non è, in senso proprio, una trasformazione geometrica giacché al suo centro O non corrisponde alcun punto proprio.