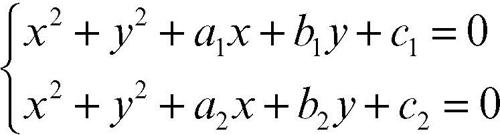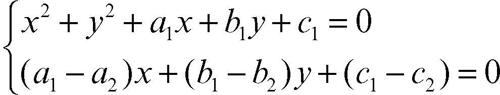circonferenze, intersezione di

circonferenze, intersezione di

circonferenze, intersezione di insieme dei punti comuni a due circonferenze del piano. Due circonferenze γ₁ e γ₂ possono avere intersezione non vuota o vuota, a seconda della loro posizione reciproca. Indicando con r₁ e r₂ i raggi delle due circonferenza e con d = O₁O₂ la distanza tra i loro centri, si hanno al riguardo i seguenti casi:

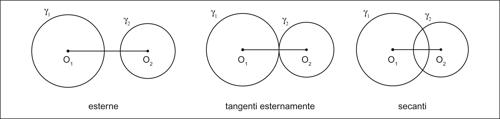
• se d > r₁ + r₂, le due circonferenze sono prive di punti comuni: γ₁ e γ₂ si dicono esterne;

• se d = r₁ + r₂, le due circonferenze hanno un punto (doppio) in comune, appartenente alla retta O₁O₂: γ₁ e γ₂ si dicono tangenti esternamente;

• se r₁ − r₂ < d < r₁ + r₂, le due circonferenze hanno due distinti punti in comune: γ₁ e γ₂ si dicono secanti;

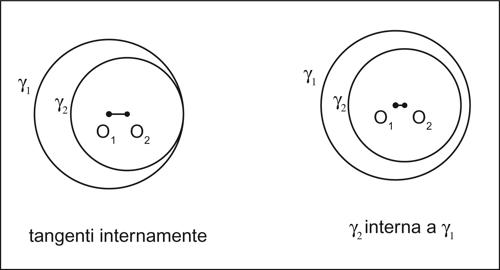
• se d = r₁ − r₂, le due circonferenze hanno un punto (doppio) in comune, appartenente alla retta O₁O₂: γ₁ e γ₂ si dicono tangenti internamente;

• se d < r₁ + r₂, le due circonferenze sono prive di punti comuni: la circonferenza di raggio minore si dice allora interna a quella di raggio maggiore; in particolare se d = 0, allora γ₁ e γ₂ sono concentriche (→ corona circolare).

Due circonferenze aventi più di due punti in comune coincidono. Dal punto di vista analitico, le intersezioni di due circonferenze si ottengono come soluzioni di un sistema del tipo

equivalente a

In accordo con le precedenti considerazioni geometriche il sistema (2), che è di secondo grado, può ammettere

• nessuna soluzione reale (circonferenze disgiunte, interne o esterne);

• due soluzioni reali e coincidenti (circonferenze tangenti internamente o esternamente);

• due soluzioni reali e distinte (circonferenze secanti).

L’aver ricondotto l’intersezione delle due circonferenze al sistema (2) significa, geometricamente, sostituire una delle due con l’→ asse radicale.