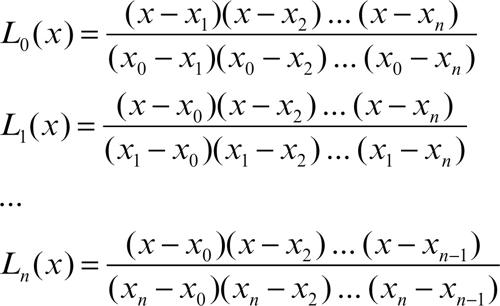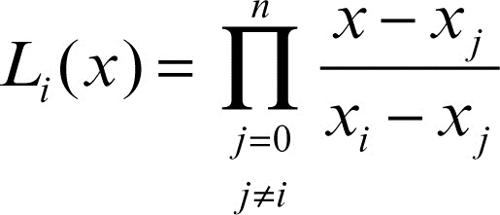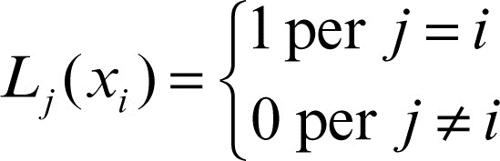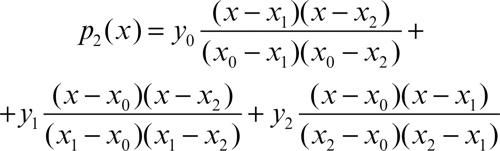Lagrange, interpolazione di

Lagrange, interpolazione di

Lagrange, interpolazione di metodo di → interpolazione per punti che utilizza una funzione polinomiale per approssimare l’andamento generale di una funzione continua y = ƒ(x) in un intervallo prefissato [a, b]. Dati n + 1 poli P_i (x_i, y_i), con x_i appartenente ad [a, b], ossia n + 1 punti noti della funzione y = ƒ(x), è possibile costruire il polinomio interpolatore di Lagrange di grado n, utilizzando le seguenti formule:

Sinteticamente:

In generale, se in un polinomio di Lagrange L_j (x) si sostituisce a x uno dei valori x_i il polinomio si annulla se x_i ≠ x_j, mentre vale 1 se x_i = x_j:

Si assume quindi come polinomio interpolatore della funzione ƒ(x) il seguente:

Per x = x₀ il polinomio di Lagrange L₀(x) vale 1, mentre gli altri termini si annullano; quindi p_n(x₀) = y₀. Analogamente, se x = x₁, L₁(x) = 1 mentre gli altri termini si annullano: quindi p_n(x₁) = y₁. Il polinomio interpolatore passa, come è richiesto, esattamente per tutti gli n + 1 poli, approssimando l’andamento della funzione y = ƒ(x). Se si scelgono due soli poli P₀ e P₁ si ottiene l’interpolazione lineare e il polinomio interpolatore di Lagrange ha la seguente forma:

Il polinomio del second’ordine fornisce la cosiddetta interpolazione quadratica:

Si può dimostrare che il polinomio interpolatore nella forma di Lagrange è ricavabile direttamente dal polinomio ottenuto con il metodo di interpolazione di → Newton. Di quest’ultimo metodo l’interpolazione di Lagrange condivide anche la stima dell’errore: indicando con la notazione ƒ_k[x₁, …, x_k] la differenza finita di ordine k relativa ai poli x₁, …, x_k si può dare una stima dell’errore nel metodo di Lagrange o resto, definito come differenza tra la funzione da interpolare e il polinomio interpolatore e(x) = ƒ(x) − p(x):

(si veda anche: → differenze finite). Essendo il metodo di Lagrange un metodo numerico, si può costruire un algoritmo, che risulta particolarmente semplice, consistente nell’esecuzione di due cicli iterativi annidati. La procedura d’interpolazione qui di seguito riportata effettua il calcolo del polinomio interpolatore; in particolare, il ciclo interno regolato dalla variabile j calcola i singoli polinomi di Lagrange L(x) e il ciclo esterno regolato dalla variabile i calcola la sommatoria. Nel corpo principale del programma che richiamerà la procedura si potranno quindi leggere sia le coordinate degli n poli che sono contenute nei vettori x[k] e y[k], sia il valore x₁ in corrispondenza del quale fare la stima.

Il metodo di Lagrange risulta conveniente quando l’ordine della funzione interpolante è già noto a priori, ossia quando si dispone di un numero limitato di punti; infatti tale metodo è molto semplice da implementare e non richiede la memorizzazione delle differenze finite divise, necessarie per esempio nel metodo di Newton (→ funzione interpolatrice).