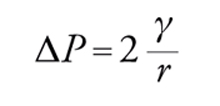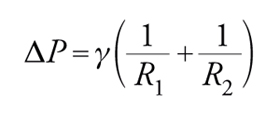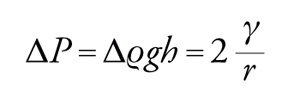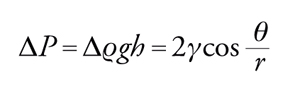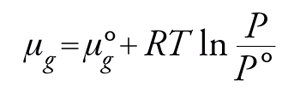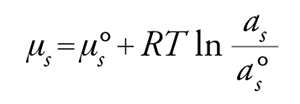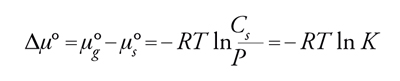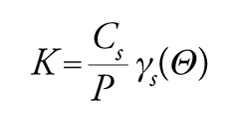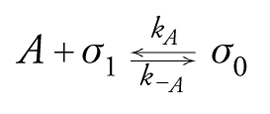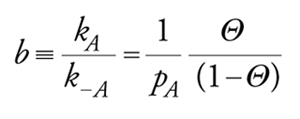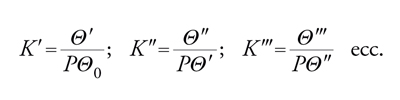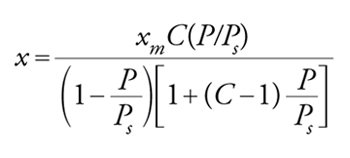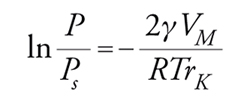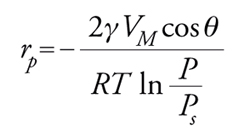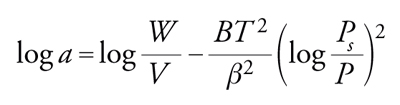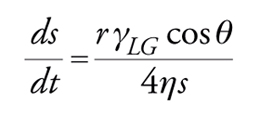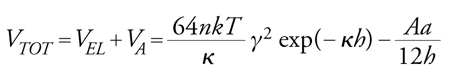Interfasi: caratteristiche chimico-fisiche
Interfasi: caratteristiche chimico-fisiche
La materia che ci circonda si presenta in tre distinti aspetti caratterizzati da diversa densità. Questi tre differenti stati della materia ‒ solido, liquido e gassoso ‒ sono caratterizzati, rispettivamente, dalla stabilità di forma e di volume, dalla sola stabilità di volume e, nel caso dei gas, da un'ulteriore perdita di consistenza in quanto un gas si espande spontaneamente fino a occupare uniformemente tutto il volume disponibile. I solidi, i liquidi e i gas possono essere elementi chimici oppure composti o ancora loro miscele. La loro esistenza nello stato in cui li osserviamo dipende soprattutto dalle condizioni di temperatura. La lava eruttata da un vulcano, per esempio, è liquida ma solidifica gradualmente raffreddandosi. Durante un certo periodo del raffreddamento si avrà quindi la coesistenza di lava fusa e di sostanze solidificate. Uno stesso elemento o uno stesso composto chimico potrà allora presentarsi distribuito in diverse fasi tra loro in equilibrio.
La superficie di confine tra fasi diverse è detta interfase ed è la sede di numerosi e spesso singolari fenomeni chimici e fisici, il cui studio rappresenta una branca piuttosto ampia della scienza.
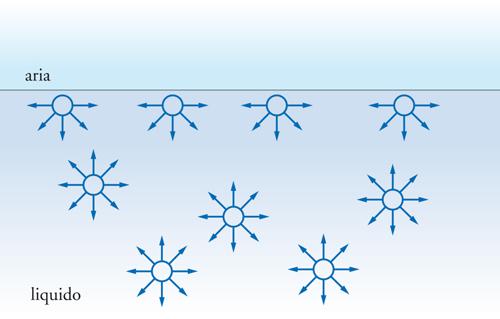
La ragione principale per cui la superficie di confine tra due fasi può dare origine a fenomeni peculiari è legata al fatto che gli atomi o le molecole che si trovano su questa superficie non possono scambiare interazioni in tutte le direzioni come gli atomi o le molecole che si trovano all'interno di ciascuna fase, ma solo con gli atomi e le molecole sottostanti.
L'insaturazione che ne deriva può essere compensata totalmente o in parte dalla possibilità di interagire con molecole presenti nella fase adiacente. Se sulla superficie di un solido, per esempio, vi sono delle cariche positive e il solido è in contatto con un gas o con un liquido le cui molecole hanno caratteristiche polari, si instaurerà a livello molecolare un'interazione diretta tra la carica positiva e la parte negativa del dipolo delle molecole e, come conseguenza, si verificherà l'adsorbimento fisico di un certo numero di molecole della fase fluida sulla superficie fino a neutralizzare l'eccesso di carica positiva del solido. Se non vi sono interazioni specifiche come quella descritta, si può avere ugualmente adsorbimento fisico grazie all'intervento delle forze di attrazione di van der Waals, che sempre si instaurano tra le molecole. Se l'interazione, invece, è molto più forte rispetto a quelle menzionate, all'interfase si potrà anche verificare una vera e propria reazione chimica tra le molecole presenti nelle due fasi che si trovano a contatto e si verificherà, in tal caso, un adsorbimento chimico. Altri numerosi fenomeni riguardano le interfasi e alcuni di questi sono spettacolari come, per esempio, la formazione di fiocchi di neve, di bolle di sapone, di schiume, dell'arcobaleno e così via. Molti fenomeni sono di importanza basilare per la realizzazione di innumerevoli prodotti e tecnologie di interesse industriale. I problemi di interfase sono cruciali, infatti, per l'industria delle vernici, degli inchiostri, dei cosmetici, dei farmaci e dei fitofarmaci, dei cementi, dei materiali compositi nonché per la separazione di minerali, per la lubrificazione, per la macinazione, per la formazione e la manipolazione di polveri.
Poiché le fasi che possono venire a contatto fra loro dando origine a delle interfasi sono quella gassosa, quella liquida e quella solida, in linea di principio si possono avere le seguenti possibili interfasi: gas-liquido, gas-solido, liquido-liquido (ovviamente per liquidi immiscibili), liquido-solido, solido-solido.
Tensione interfacciale e fenomeni relativi
Lo sbilanciamento delle forze di attrazione all'interfaccia, quale, per esempio, quello illustrato nella fig. 1, ha come conseguenza che il maggior numero possibile di molecole abbandona la superficie per raggiungere una condizione termodinamicamente più favorevole all'interno del liquido. La superficie interfacciale mostra cioè la tendenza a contrarsi spontaneamente. Per questa ragione le gocce di liquido o le bolle di sapone tendono ad assumere una forma sferica che è quella che garantisce la minima superficie a parità di volume. Per contrastare questa tendenza e creare nuova superficie bisogna compiere un lavoro proporzionale all'area prodotta. Per un incremento dA della superficie realizzato a pressione e temperatura costanti, il lavoro dL si identifica con la variazione di energia libera dG e può essere così scritto:
[1] dL=dGT=γdA
dove γ, il coefficiente di proporzionalità, è la tensione superficiale espressa in energia per unità di area. Questa grandezza può anche essere definita come una forza per unità di lunghezza. Due esempi sono utili a precisare meglio questo concetto. Consideriamo nel primo caso un film di sapone teso all'interno di un telaio di metallo che abbia un'estremità mobile di lunghezza l. In tal caso occorre applicare una forza per estendere il film. Se il valore di questa forza per unità di lunghezza è indicato con γ, il lavoro da compiere per spostare il cursore per una distanza dx sarà:
[2] dL=2γldx.
Il secondo esempio riguarda una bolla di sapone. Immaginiamo qui la tensione superficiale come un'energia per unità di superficie. Il lavoro per un incremento di superficie corrispondente a un aumento del raggio r della bolla pari a dr può essere calcolato innanzitutto dal lavoro di espansione ΔP4πr2, che va eguagliato all'energia libera dG=γdA=8πrγdr. Ne deriva che (equazione di Laplace):
[3] formula.
Questa equazione mostra che la pressione interna a una bolla rispetto all'esterno è maggiore per bolle piccole rispetto a bolle grandi. Perciò, se due bolle di diversa dimensione vengono a contatto si ha il paradosso che la bolla piccola si sgonfia favorendo la crescita della bolla più grande. L'equazione di Laplace [3] è un caso molto particolare poiché si riferisce a una geometria perfettamente sferica. In generale, per descrivere una generica superficie curva è necessario ricorrere ad almeno due raggi di curvatura R1 e R2. L'equazione [3] diventa in tal caso:
[4] formula
nota come equazione della capillarità di Young-Laplace.
===La misura della tensione superficiale===
Abbiamo visto che un liquido si comporta come se fosse ricoperto da una pelle contrattile. Ogni tentativo di estendere la superficie di questa pelle è contrastato dalla tensione superficiale. I metodi di misura della tensione superficiale, perciò, sono tutti basati sulla misura delle forze che si devono applicare per vincere la tensione superficiale come negli esempi descritti.
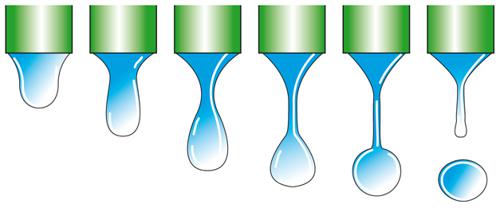
Metodo basato sul peso di una goccia che cade dalla punta di un capillare. - Il peso W della goccia è correlato con la tensione superficiale attraverso la relazione:
[5] =2πrγf
dove f=F(r/V1/3) è un fattore di correzione dovuto al fatto che, come si vede nella fig. 2, solo una parte del liquido emerso dal capillare va a formare la goccia.
Metodo della misura della pressione massima di bolla. - Attraverso un capillare viene fatto passare lentamente un gas inerte che gonfia una bolla di gas. Si forma una superficie emisferica che raggiunge un valore minimo del raggio quando r è il raggio esterno del tubo. Per r minimo si ha la pressione massima e si può applicare la relazione [3] per calcolare γ, introducendo anche in questo caso dei termini correttivi per una valutazione più accurata.
Metodo basato sulla valutazione della forma di gocce o bolle statiche. - Una goccia che pende da un capillare o una bolla di gas emergente da un orifizio assumono un profilo che dipende in modo complesso ma prevedibile dalla tensione superficiale. Analoghe valutazioni possono essere fatte per gocce o bolle sessili.
Tensiometro di De Nouy. - Si misura in questo caso la forza da applicare per staccare dalla superficie di un liquido un anello di filo metallico molto sottile. Il metodo è soggetto a errori e richiede la valutazione di un fattore di correzione.
Bilancia di Wilhelmy. - Concettualmente il metodo è simile al precedente, ma ne differisce per il fatto che invece di un anello di filo metallico si utilizza un piatto che, venendo a contatto con il liquido, richiede per il distacco un soprappeso di (γp) essendo p il perimetro del piatto.
Innalzamento capillare. - Questo metodo verrà trattato in dettaglio nel prossimo paragrafo.
Bagnabilità, angolo di contatto, capillarità
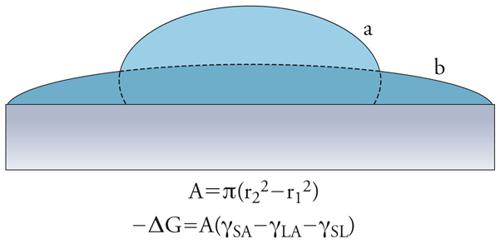
L'innalzamento del livello dell'acqua in tubi sottili era già stato osservato da Leonardo da Vinci. Il fenomeno è noto come capillarità e per comprenderne la natura è opportuno definire prima di tutto la bagnabilità di una superficie e l'angolo di contatto. Rispetto alla bagnabilità (wetting), possono verificarsi tre diverse situazioni: (a) bagnatura per adesione (fig. 3), nella quale all'interfaccia solido-aria viene sostituita l'interfaccia solido-liquido; (b) bagnatura per spandimento (fig. 4), nella quale il liquido si espande sul solido aumentando l'area interfacciale; (c) bagnatura per immersione, nella quale il solido viene immerso completamente nel liquido.
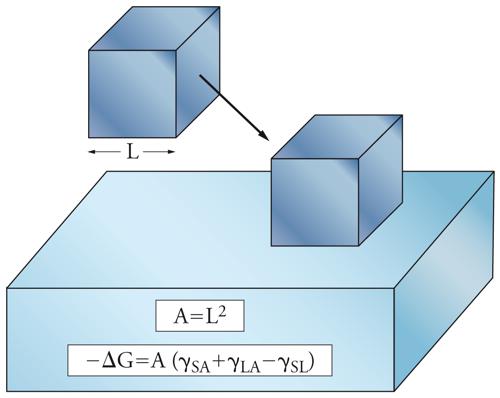
Nelle figure 3 e 4, sono riportate anche le variazioni di energia libera che si accompagnano alle prime due situazioni descritte. Queste espressioni si calcolano valutando l'area della superficie di interfase, e considerando che, in seguito alla bagnatura, cambia la natura delle interfasi coinvolte (SA=solido-aria, LA=liquido-aria, SL=solido-liquido): si riduce l'interfaccia SA, compare o aumenta quella SL, mentre, a seconda dei casi, l'interfaccia LA può ridursi o aumentare. Nel terzo caso (immersione), invece, si ha la sostituzione dell'interfase SA con quella SL; per il caso semplificato di un cubo di lato L, l'area è pari a 6L2 e la variazione di energia libera è data da:
[6] −ΔG = 6L2(γSA − γSL).
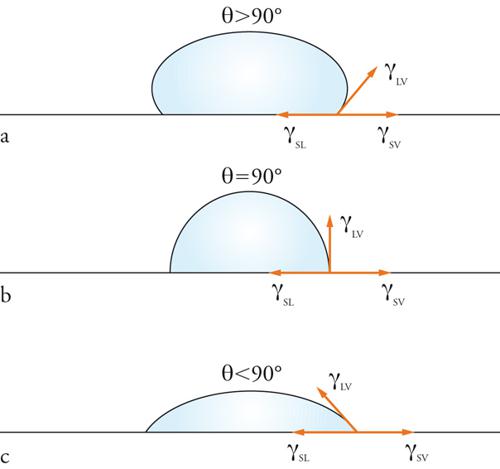
Se poniamo una goccia di un liquido su una superficie solida, questa si spande più o meno e bagna il solido spostando il gas che lo ricopriva. Al punto di confine estremo della goccia abbiamo la coesistenza delle tre fasi solida, liquida e gassosa (vapore o aria). Esattamente in questo punto si misura l'angolo di contatto. Se il liquido bagna il solido questo angolo è molto piccolo (minore di 90°), se viceversa la superficie è repellente nei confronti del liquido, l'angolo diventa elevato e la goccia tende ad assumere la forma sferica (fig. 5).
L'angolo di contatto dipende dall'equilibrio tra le tensioni superficiali delle tre diverse interfasi: solido-liquido γSL, liquido-vapore γLV, solido-vapore γSV. Il bilancio delle forze in gioco è espresso dall'equazione:
[7] γSL−γSV+γLVcosθ=0
dove θ è l'angolo di contatto. Se θ≅0 si ha completa bagnabilità. Solo γLV può essere agevolmente misurato, gli altri termini possono essere determinati solo indirettamente confrontando questa espressione con quella che si ottiene nella valutazione del lavoro di adesione di un liquido sulla superficie di un solido (equazione di Duprè):
[8] WSL=γSV+γLV−γSL
WSLG=γLV(1+cosθ).
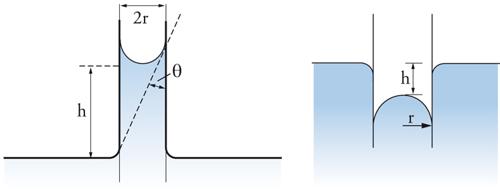
Affrontiamo ora il problema della capillarità. Se un liquido bagna perfettamente le pareti di un capillare di forma cilindrica (angolo di contatto pari a 0), il livello del liquido nel capillare si innalza di un'altezza h tale da bilanciare la differenza di pressione dovuta alla tensione interfacciale (fig. 6 a sinistra), fornita dall'equazione di Young e Laplace. Si forma allora un menisco concavo il cui raggio di curvatura è uguale al raggio del capillare e l'equazione [4] si riduce alla [3] con r pari al raggio del capillare. In questa relazione ΔP è equivalente alla perdita di carico idrostatica della colonna liquida nel capillare, pertanto:
[9] formula,
dove Δϱ indica la differenza di densità tra fase liquida e fase gassosa, g è l'accelerazione di gravità e h è l'innalzamento capillare. Nel caso in cui il liquido non bagni affatto le pareti del capillare (angolo di contatto pari a 180°), si ottiene invece un menisco convesso e un abbassamento del livello nel capillare (fig. 6 a destra). L'equazione di bilancio delle forze porta, comunque, al medesimo risultato.
Se l'angolo di contatto ha un valore intermedio è facile dimostrare che:
[10] formula.
La misura dell'angolo di contatto fornisce, quindi, un'indicazione quantitativa della bagnabilità di una superficie.
===Effetto dei tensioattivi sulla tensione interfacciale===
La proprietà fondamentale più nota dei tensioattivi è rappresentata dalla loro capacità di ridurre la tensione superficiale alle interfasi. Ciò determina una drastica riduzione del lavoro necessario per estendere l'area interfacciale, per realizzare e mantenere un sistema disperso (schiuma, emulsione o sospensione) e per favorire la bagnabilità di una superficie. Il tensioattivo può inoltre svolgere un'azione detergente nei confronti di una superficie o di una fibra e può condizionare la superficie trasformandola da idrofila in idrofoba o viceversa.
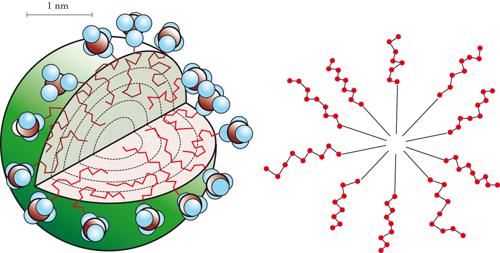
Questi e altri comportamenti peculiari dei tensioattivi sono dovuti alla loro struttura asimmetrica costituita da una parte apolare (idrofoba), in genere costituita da una catena idrocarburica più o meno lunga, e una parte polare (idrofila). I tensioattivi vengono classificati, in genere, esclusivamente per le caratteristiche della loro parte idrofila che può essere ionica (anionica, cationica e anfotera) oppure non ionica (catene polietossiliche, catene poliglucosidiche). Grazie alla loro particolare struttura i tensioattivi si dispongono preferenzialmente all'interfase, con la parte polare a contatto con la fase più polare e la parte apolare a contatto con la fase meno polare. Le molecole di tensioattivo si aggregano poi fra loro formando delle micelle, che possiedono normalmente una struttura sferica (minimo numero di aggregazione per un certo volume) (fig. 7). Le micelle cominciano a formarsi per un certo valore di concentrazione del tensioattivo in soluzione, che è caratteristico del tipo di tensioattivo e viene indicato come CMC (Concentrazione micellare critica). Le micelle hanno la prerogativa diessere sistemi estremamente dispersi avendo diametridell'ordine di 20÷40 Å. Nel cuore della micella posso-no essere ospitate molecole normalmente insolubili nel solvente; in questo modo la micella favorisce la solu-bilizzazione di olio in acqua o viceversa. Sono possibili anche aggregazioni diverse e assai più complesse con formazione di strutture lamellari, vescicole, cristalli liquidi e così via.
Gli stessi tensioattivi danno luogo in olio a micelle inverse che hanno la parte polare rivolta verso il cuore della micella. Il tensioattivo può quindi essere usato sia per sgrassare una superficie sia per eliminarne l'umidità. Il peso relativo della parte idrofoba rispetto a quella idrofila influisce sulla solubilità del tensioattivo in acqua o in olio e sulla dipendenza della solubilità dalla temperatura. La parte idrofoba e quella idrofila devono essere opportunamente bilanciate per garantire sia la solubilità sia la funzione che si vuole far esercitare al tensioattivo. Per valutare quantitativamente questo aspetto è stata messa a punto da William C. Griffin una scala arbitraria denominata HLB (Hydrophilic lipophilic balance). Questa scala assume valori compresi tra 1 e 20. A 1 corrisponde il sistema, assolutamente lipofilo, acido oleico e a 20 il composto idrofilo oleato di sodio. Il valore di HLB può essere calcolato, nota la struttura molecolare del tensioattivo, con metodi ai contributi di gruppo oppure può essere determinato sperimentalmente. Esistono dei valori ottimali di HLB per ottenere buone prestazioni dal tensioattivo, come si può apprezzare nella tab. 1.
I tensioattivi si possono adsorbire sulla superficie di un solido modificandone in modo netto le caratteristiche superficiali e influenzandone quindi drasticamente il comportamento nei fenomeni di bagnatura (wetting), adesione, lubrificazione, corrosione, le proprietà elettriche (agenti antistatici), l'adsorbimento di altri soluti (tinteggiatura), la sospensione. La capacità delle molecole di tensioattivo di disporsi nel modo desiderato all'interfaccia liquido-solido dipende dalle caratteristiche del solido, del tensioattivo e del solvente nonché dalla temperatura e dalla concentrazione.
I tensioattivi, infine, sono largamente impiegati nella detergenza, processo in cui sono coinvolti una serie di fenomeni che hanno come risultato la rimozione dello sporco da una superficie solida. Il meccanismo con cui ciò avviene è complesso e prevede l'adsorbimento del tensioattivo sia sulla superficie da pulire sia sulle particelle di sporco, di cui favorisce così la rimozione attraverso la riduzione della tensione interfacciale e l'inglobamento e la solubilizzazione nelle micelle, se si tratta di olio o grasso, oppure la sospensione in fase acquosa se si tratta di particelle solide. Tutti i fenomeni fin qui descritti (bagnamento, adesione, spandimento, emulsione, sospensione) giocano un ruolo durante la fase di lavaggio.
Interfasi gas-solido
Adsorbimento fisico, misura dell'area specifica e della porosità
Questo tipo di adsorbimento è caratterizzato da interazioni fra adsorbente e adsorbato del tipo di van der Waals. Possiamo dire che si ha equilibrio di adsorbimento quando i potenziali chimici di una sostanza nello stato adsorbito e nel gas sono uguali: μs=μg.
Essendo, per basse pressioni P
[11] formula,
se si pone P° =1 atm
[12] μg=μ°g+RTlnP.
Per il gas adsorbito analogamente vale:
[13] formula.
dove as è l'attività del gas adsorbito e a°s è l'attività nello stato standard. Per ricoprimenti prossimi a 0, l'attività si confonde con la concentrazione, per cui as=Cs, mentre a°s=1. Si avrà quindi
[14] μs=μ°s+RTlnCs.
Considerando l'uguaglianza dei potenziali chimici avremo:
[15] formula,
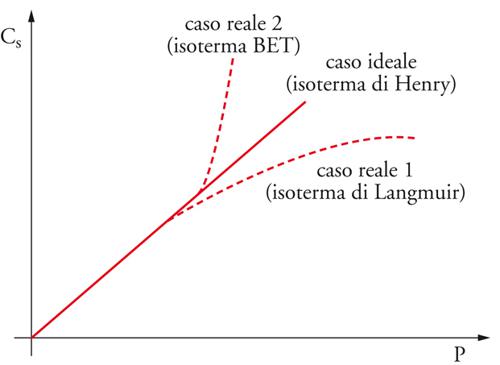
con K=Cs/P costante di equilibrio di adsorbimento. Questa espressione rappresenta il caso ideale noto come isoterma di Henry. Per elevati gradi di ricoprimento as≠Cs e quindi:
[16] formula,
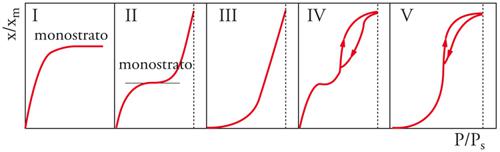
dove γs(Θ) è il coefficiente di attività e Θ il grado di ricoprimento. In generale, si avranno tre possibili andamenti di Cs in funzione di P, illustrati nel grafico di fig. 8.
Più in particolare, l'espressione analitica delle isoterme reali richiede la definizione della funzione γs=γs(Θ). Le possibili isoterme reali sono di cinque tipi e sono rappresentate nella fig. 9: (a) il primo tipo (I) detta isoterma di Langmuir, riguarda i sistemi in cui l'adsorbimento si limita al monostrato e rappresenta perciò una situazione di riferimento per gli altri casi; (b) il secondo tipo (II) indica la formazione di un numero indefinito di strati dopo la formazione del monostrato, che termina nel punto di flesso; (c) nel terzo tipo (III) la forma convessa è dovuta al fatto che il calore di adsorbimento è qui molto basso rispetto al calore di condensazione, e si ha formazione di un numero indefinito di strati; (d) il quarto tipo (IV) è una variante della II con la formazione di un numero finito di strati per riempimento completo di capillari; lo svuotamento dei capillari avviene con modalità diverse dal riempimento (isteresi nel fenomeno adsorbimento-desorbimento); (e) il quinto tipo (V) è una variante della III a numero definito di strati, dove nuovamente si presenta l'isteresi. I tipi II-V sono anche dette isoterme di BET dal nome degli autori Sthephen Brunauer, Paul H. Emmett ed Edward Teller.
Da questo rapido esame si può concludere che se l'isoterma di Henry rappresenta il riferimento ideale per la raccolta di dati termodinamici, l'isoterma di Langmuir rappresenta un riferimento importante per le isoterme reali. Essa rappresenta la saturazione progressiva del monostrato su di un solido con superficie di caratteristiche uniformi in assenza di interazioni laterali tra le molecole. Si potrà pensare all'adsorbimento come a una pseudo-reazione:
[17] formula
dove σ1 e σ0 sono rispettivamente i siti liberi e quelli occupati. Vale σ1+σ0=σtot e ponendo Θ=σ0/σtot avremo che σ1/σtot=(1−Θ). Le velocità di adsorbimento e desorbimento saranno:
[18] rA=kApAσ1=kApA(1−Θ)σtot
[19] r−A=k−Aσ0=k−AΘσtot
dove pA è la pressione parziale di A, e la velocità netta di adsorbimento sarà:
[20] r=rA−r−A=kApAσtot(1−Θ)−k−AΘσtot.
All'equilibrio r=0 e quindi (isoterma di Langmuir)
[21] formula,
essendo b la costante di equilibrio di adsorbimento. Date le premesse imposte per la validità della isoterma di Langmuir, essa è valida sia per adsorbimenti fisici localizzati a forte interazione specifica sia, a maggior ragione, per adsorbimenti chimici su siti con caratteristiche uniformi.
Le isoterme di BET prevedono l'adsorbimento di più strati molecolari. Nello sviluppo della teoria si considera: (a) superficie uniforme; (b) assenza di interazioni laterali; (c) adsorbimento localizzato. Per l'interpretazione delle isoterme si applica anche qui un modello quasi-chimico per definire l'equilibrio:
[22] Vapore+superficie libera ⇆ complessi singoli S1
Vapore+complessi singoli ⇆ complessi doppi S2
Vapore+complessi doppi ⇆ complessi tripli S3
Da cui:
[23] formula
dove Θ0 è la frazione di superficie libera. La quantità adsorbita sarà:
[24] x=xm(Θ′+2Θ″+3Θ‴+…),
dove xm è la capacità del monostrato in mol/g. Attraverso una serie di passaggi matematici si arriva alla seguente espressione per l'isoterma di BET:
[25] formula
dove Ps è la tensione di vapore della specie adsorbita. La [25] può essere posta in forma linearizzata: ponendo in grafico (P/Ps)/[x(1−(P/Ps))] contro P/Ps si ottiene una retta la cui pendenza è [(C−1)/xmC] e la cui intercetta è 1/xmC. C è un parametro che rappresenta l'interazione netta tra le molecole di gas e la superficie del solido. Per C≫1 e P lontano da Ps si avrà una isoterma del tipo I, per C〈1 si avrà l'isoterma di tipo III, nei casi intermedi l'isoterma di tipo II.
L'isoterma BET è utile per determinare la superficie specifica dei solidi per adsorbimento sulla loro superficie di un gas di cui si conosca l'ingombro sterico nel monostrato. La superficie occupata dalle molecole di azoto a 77 K, per esempio, è: ωN2=16,2 Å2. La conoscenza, quindi, del valore di xm è fondamentale allo scopo e la superficie specifica del solido sarà: SBET=xmωN2NA dove NA è il numero di Avogadro.
Le isoterme di tipo IV e V sono caratterizzate da fenomeni di isteresi dovuti a condensazione del gas all'interno dei mesopori. La forma geometrica della zona di isteresi è in relazione con le caratteristiche dei pori (a forma di provetta, di bottiglia, ecc.). Questo fenomeno può essere interpretato con l'equazione di Kelvin che deriva dall'eguaglianza dei potenziali chimici in fase liquida e in fase vapore:
[26] formula
dove rK=raggio medio di curvatura del menisco; γ=tensione superficiale del liquido; VM=volume molare; P/Ps==pressione relativa a cui si ha condensazione. Ricordando poi che rp=rKcosθ dove θ=angolo di contatto e rp=raggio del poro:
[27] formula.
Lo studio della forma dell'isoterma insieme all'impiego dell'equazione di Kelvin permette di definire la distribuzione della dimensione dei pori. I pori possono essere classificati in micropori, con raggio equivalente r〈20 Å, mesopori, con raggio 20〈r〈1000 Å, e macropori, con r>1000 Å. Il raggio equivalente è pari a 2×raggio idraulico=2×sezione del poro/perimetro.
Oltre che da misure di adsorbimento, la porosità si può determinare in modo più diretto con il porosimetro a mercurio: si introduce del mercurio nei pori, sotto pressione, si costruisce una curva che lega la pressione applicata alla quantità di mercurio che penetra nei pori e, per pori a sezione circolare, si ricava il raggio corrispondente a ogni livello di pressione mediante l'equazione di Laplace nella forma [9].
Le isoterme descritte non sono valide per superfici prevalentemente costituite da micropori, per esempio per zeoliti o carbone attivo. In tal caso è valida, per l'adsorbimento fisico, l'isoterma di Dubinin-Radushkevic che tiene conto del fatto che nei micropori si verifica condensazione:
[28] formula,
dove W è il volume totale dei pori; a la quantità di adsorbato per unità di volume di adsorbente; V il volume molare dell'adsorbato; aV=W il volume occupato dall'adsorbato; B la costante che dipende dal volume dei pori; β il coefficiente di affinità.
Adsorbimento chimico
L'adsorbimento chimico comporta l'instaurarsi di un vero e proprio legame chimico fra l'adsorbato e l'adsorbente. Ciò può avvenire, per esempio, in seguito alla dissociazione della molecola per effetto di un sito acido o basico, oppure per legame dativo tra un doppietto elettronico libero dell'adsorbato e un metallo di transizione o mediante altri tipi di interazione chimica. Se la superficie solida si può considerare piuttosto uniforme, in genere l'isoterma di Langmuir è adeguata a rappresentare l'adsorbimento chimico. In realtà spesso le superfici non sono caratterizzate da elevata uniformità (fig.10) e le caratteristiche dell'adsorbimento chimico possono variare con il grado di ricoprimento.
Se si vuole favorire un processo di chemiadsorbimento è necessario tener presente che esso può avvenire a temperature relativamente elevate, essendo, come le normali reazioni chimiche, un fenomeno attivato. L'adsorbimento chimico può essere classificato come associativo o dissociativo a seconda che la molecola conservi o meno la sua integrità nel processo.
Interfasi liquido-solido
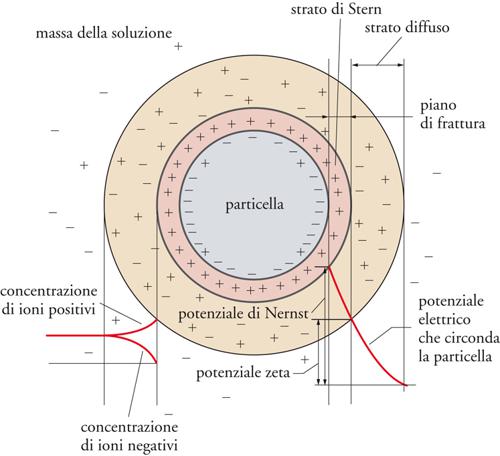
Nel discutere le interfasi liquido-solido dobbiamo distinguere tra i sistemi che definiamo normali e quelli a elevata dispersione (in genere sospensioni). Per sistemi normali possiamo osservare, innanzitutto, che il solido si può distinguere per forma (fibra, superficie piana, granuli), dimensione, porosità, polarità e composizione chimica, e può, inoltre, presentare una superficie con caratteristiche più o meno eterogenee. In particolare, sulle superfici solide si possono accumulare delle cariche elettriche, sia per la natura stessa della superficie sia in seguito all'adsorbimento di tensioattivi ionici. In presenza di acqua, la carica superficiale è compensata da controioni che danno origine a un doppio strato elettrico detto di Gouy-Chapman. La parte più interna (strato di Stern) è costituita da un guscio di controioni che schermano le cariche superficiali. Lo strato successivo, di carica opposta, è più diffuso. Tutto ciò è rappresentato schematicamente nella fig. 11. La carica elettrica dello strato di Stern esercita un'azione repulsiva che rende abbastanza stabili i sistemi di questo tipo.
Il contatto di un solido con un solvente (che può essere acqua, ma anche un composto organico polare o apolare, protico o aprotico) dà origine a un velo monomolecolare di solvente adsorbito sul solido. L'adsorbimento sulla superficie dei solidi può avvenire per interazioni di vario tipo: (a) interazioni dovute a forze di van der Waals; (b) interazioni di tipo elettrostatico tra cariche di segno opposto; (c) interazioni dovute a cariche di polarizzazione; (d) interazioni dovute a legami a idrogeno. Al solito, se l'interazione è più forte si può avere anche adsorbimento chimico. È difficile però valutare quantitativamente l'adsorbimento che si verifica per contatto tra una fase liquida e un solido, a meno che esso non riguardi molecole disciolte nel solvente che viene a contatto con il solido, per le quali il solido abbia un'elevata affinità. In questo caso si può studiare l'adsorbimento determinando la quantità adsorbita di sostanza dalla variazione di concentrazione della soluzione posta a contatto con il solido. A volte la sostanza che si adsorbe sulla superficie è un tensioattivo. La modalità di adsorbimento in questo caso può dare origine, secondo alcuni autori, a 16 diversi tipi di isoterme la cui classificazione è utile per riconoscere il meccanismo di adsorbimento. Abbiamo già visto le trattazioni generali riguardanti la bagnabilità, la capillarità, l'angolo di contatto e l'abbassamento della tensione superficiale per effetto dei tensioattivi. Bisogna dire che in alcuni casi, come per esempio per la bagnabilità delle fibre, non è facile misurare l'angolo di contatto. In questi casi si misura la velocità di imbibizione (test di Draves) che è correlata con l'angolo di contatto e con la tensione superficiale attraverso l'espressione:
[29] formula
dove s è la distanza che l'acqua, posta a contatto con la fibra, percorre per capillarità (η, viscosità; r, raggio medio dei pori capillari).
Per i sistemi costituiti da piccole particelle di solido disperso in un liquido (sospensioni) valgono le considerazioni svolte, ma bisogna considerare la stabilità della sospensione. Poiché vari aspetti relativi alla stabilità sono simili per le sospensioni e le emulsioni, l'argomento verrà trattato poco oltre per entrambi i casi.
Interfasi liquido-liquido
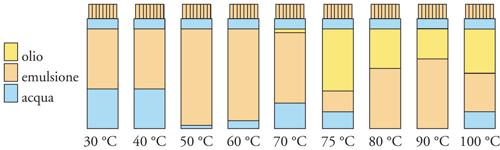
La formazione di interfasi liquido-liquido si verifica quando vengono a contatto due liquidi immiscibili. Anche qui bisogna distinguere tra sistemi normali e sistemi dispersi. Per i sistemi normali si possono fare considerazioni simili a quelle già riportate circa la tensione superficiale, il lavoro di adesione, quello di spandimento, l'angolo di contatto e così via. Per ottenere sistemi dispersi bisogna ricorrere all'impiego di tensioattivi che, riducendo la tensione interfacciale, favoriscono la formazione di emulsioni. Abbiamo già visto a questo proposito l'importanza di definire la solubilità e il valore di HLB di un tensioattivo. La solubilità dei tensioattivi varia però con la temperatura, e questo effetto non è considerato nel valore di HLB. È stato evidenziato come un'emulsione possa cambiare le proprietà di solubilità, passando da solubilità in acqua a solubilità in olio e viceversa, in uno stretto intervallo di temperatura. La temperatura che contraddistingue questo fenomeno si chiama PIT (Phase inversion temperature) ed è la temperatura alla quale un'emulsione di olio in acqua (acqua+olio in eguale quantità +5% di tensioattivo) inverte le sue caratteristiche diventando un'emulsione di acqua in olio (fig. 12). A questa temperatura si registra il minimo di tensione interfacciale del sistema poiché le tendenze idrofila e lipofila del tensioattivo sono perfettamente bilanciate. La PIT, quindi, dipende dalla struttura del tensioattivo ed è in relazione con la stabilità dell'emulsione. In vicinanza della PIT, infatti, l'emulsione è poco stabile e fornisce utili indicazioni sulle modalità ottimali di preparazione dell'emulsione.
Un altro parametro importante per caratterizzare un'emulsione è l'EIP (Emulsion inversion point), pari, per una data temperatura, ai cm3 di acqua per cm3 di olio occorrenti per invertire l'emulsione. L'EIP è un indice del grado di idratazione del film interfacciale, anch'esso in relazione con la stabilità dell'emulsione. Esso tende a diminuire con l'HLB, raggiungendo un valore di minimo cui corrisponde il massimo di stabilità delle emulsioni di olio in acqua.
Stabilità di sistemi dispersi (emulsioni, sospensioni)
Emulsioni e sospensioni sono sistemi termodinamicamente instabili, nel senso che i costituenti di base hanno tendenza a separarsi spontaneamente. Realizzare la loro stabilità significa, quindi, contrastare cineticamente la tendenza alla separazione dei costituenti. Gli aspetti cinetici di stabilità delle emulsioni e delle sospensioni sono stati affrontati dalle teorie sviluppate da Marian Smoluchowski e Nikolaj Fuchs.
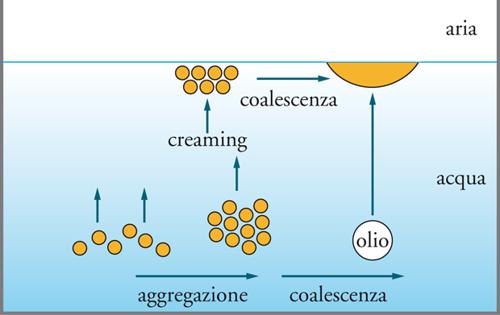
Le emulsioni, per esempio, possono rompersi attraverso un meccanismo che prevede tre fasi: (a) creaming, aggregazione dovuta all'effetto di gravità; (b) flocculazione, aggregazione dovuta a forze attrattive; (c) coalescenza, cioè la formazione di goccie sempre più grandi. Il meccanismo è illustrato nella fig. 13.
Analogamente, le sospensioni possono, a loro volta, dare origine ad aggregazione e flocculazione. La forza di gravità fa sedimentare più o meno velocemente le particelle che, entrando l'una nella sfera di interazione dell'altra, si attraggono fino a formare aggregati più o meno compatti. Per contrastare i fenomeni di aggregazione bisogna indurre una repulsione fra le particelle di solido introducendo, per esempio, cariche elettriche dello stesso segno sulla loro superficie oppure favorendo un meccanismo della repulsione sterica ottenuto grazie all'adsorbimento di molecole voluminose. I due fenomeni menzionati non sono in contrapposizione e possono perciò essere adottati contemporaneamente. I tensioattivi non ionici, per esempio, stabilizzano le sospensioni esclusivamente attraverso il meccanismo di repulsione sterica, mentre i tensioattivi ionici attraverso quello della repulsione elettrostatica.
L'instabilità di emulsioni e sospensioni è originata dalle forze che agiscono sulle particelle favorendone o impedendone il contatto. Queste forze possono essere di origine idrodinamica o colloidale. La particella è normalmente soggetta a movimento per diffusione, conseguenza a livello macroscopico dei moti browniani e dell'agitazione, o per sedimentazione, originata dal campo gravitazionale. Le particelle, una volta giunte a contatto ravvicinato a seguito di questi moti, possono poi attrarsi o respingersi per l'intervento di forze attrattive (di van der Waals) o di forze repulsive (elettrostatiche e steriche). La teoria DLVO introdotta da Boris V. Derjaguin e Lev D. Landau e, indipendentemente, da Evert J.W. Verwey e Jan Th.G. Overbeek, interpreta quantitativamente il bilancio tra le forze attrattive di van der Waals e quelle repulsive elettrostatiche, formando una espressione per il potenziale di interazione. Nel caso più semplice dell'interazione tra due particelle cariche uguali vale:
[30] formula,
dove VA è il potenziale di interazione attrattiva, VEL il potenziale di interazione repulsiva di origine elettrostatica, h la distanza fra i centri delle particelle, a la dimensione delle particelle, n la concentrazione ionica, k la costante di Boltzmann, κ il reciproco dello spessore del doppio strato elettrico, γ il parametro di interazione variabile tra 0 e 1, A la costante di Hamaker.
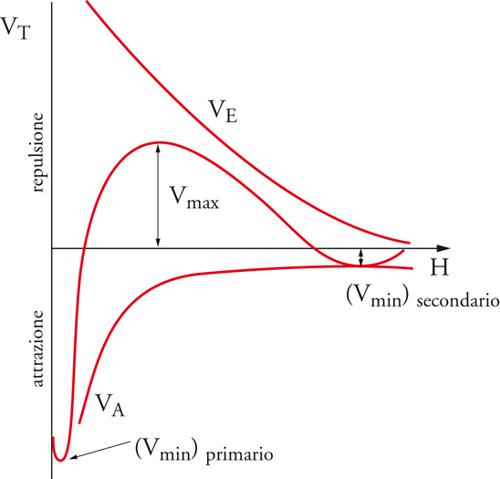
L'andamento del potenziale totale rispetto alla distanza fra le particelle è la risultante degli andamenti di VA e VEL e presenta due minimi, uno, detto secondario, corrispondente alla formazione temporanea di aggregati di flocculazione facilmente ridisperdibili, e uno profondo, detto primario, corrispondente alla coagulazione irreversibile (fig. 14). La barriera di potenziale che si oppone alla coagulazione sarà tanto più elevata quanto più elevato è il potenziale di repulsione elettrostatica VEL.
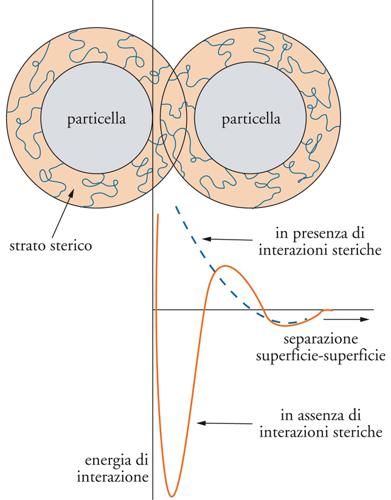
Ė possibile stabilizzare le sospensioni anche adsorbendo sulla superficie del solido molecole di grossa dimensione (stabilizzazione sterica), per esempio tensioattivi non ionici. Numerose teorie sono state elaborate per descrivere il fenomeno, tra le quali la teoria HVO (Hesselink, Vrij e Overbeek). La repulsione sterica agisce sia mediante restrizione del volume, per la quale le molecole adsorbite sono confinate quando le particelle solide si avvicinano troppo, sia per effetto osmotico, dovuto all'aumento locale di concentrazione di tensioattivo. Avremo quindi: VTOT=VA+VEL+(VOS+VVR). Quando la repulsione elettrica è nulla(VEL=0), come nel caso dei tensioattivi non ionici, la curva di potenziale risulta priva di minimo primario e non si può perciò verificare la coagulazione irreversibile (fig. 15).
Interfasi gas-liquido e liquido-gas
Per quanto riguarda le interfasi gas-liquido, abbiamo già parlato della formazione di bolle e di film liquidi quali sistemi utili per la determinazione della tensione interfacciale, esaurendo così la descrizione dei sistemi normali. Per quanto riguarda invece i sistemi dispersi, due casi sono degni di nota: le schiume (dispersione di gas in un liquido) e gli aerosol (dispersione di liquido in un gas).
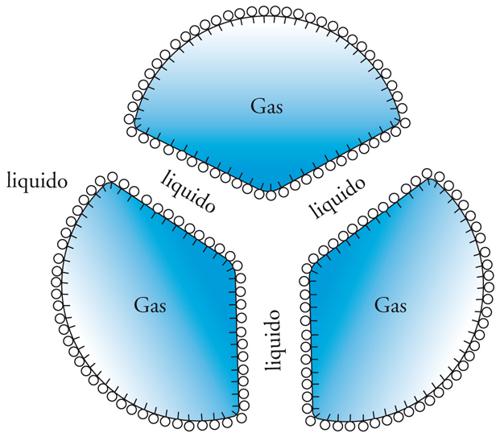
Una schiuma si può paragonare in certi casi a un'emulsione in cui la fase dispersa sia gassosa invece che liquida. Come per le emulsioni, la formazione di schiuma richiede l'intervento di un tensioattivo perché si realizzi un sistema relativamente stabile. Si può avere sia la formazione di bolle sferiche molto piccole separate fra loro da un film liquido (emulsione di gas), sia di bolle relativamente grandi che aderiscono fra loro formando strutture poliedriche. Il liquido è ridotto a un film sottile che separa le strutture poliedriche. Le schiume hanno strutture definite studiate in dettaglio da Joseph-A.-F. Plateau e da Josiah W. Gibbs. Quando tre film di liquido si incontrano come nella fig. 16, per esempio, formano tre angoli uguali fra loro di 120°. Ogni film ha una tendenza a contrarsi con una forza pari a 2γ per unità di superficie, e quindi tre forze identiche si bilanciano fra loro e il sistema è stabile solo se si formano angoli uguali, appunto di 120°. Questo comportamento è giustificato dall'esigenza termodinamica di minimizzare l'area superficiale del film liquido tra le bolle. Anche la struttura di sistemi con quattro o più bolle si assesta in modo da avvicinarsi il più possibile a una condizione geometrica stabile. Per distruggere o rendere instabile una schiuma bisogna agire sul film liquido che separa le bolle di gas utilizzando per esempio delle sostanze che siano incompatibili con la formazione del film o che ne distruggano l'integrità.
Un altro importante sistema con elevata superficie interfacciale è costituito dagli aerosol, che sono sospensioni di piccole particelle di liquido o solido in un gas. Gli aerosol possono essere studiati per le diverse modalità di generazione (reazioni chimiche, nucleazione in vapori supersaturi, impiego di eiettori spray), per gli effetti di coagulazione o per la stabilizzazione mediante cariche elettriche.
Bibliografia
Adamson 1990: Adamson, Arthur W., Physical chemistry of surfaces, 5. ed., New York-Chichester, Wiley, 1990.
Baglioni 2000: Baglioni, Piero - Berti, Debora - Bonini, Massimo, Preparation and stability of emulsion, "Chimica & industria", 7, 2000, pp. 743-750.
Brunauer 1938: Brunauer, Stephen - Emmett, Paul H. - Teller, Edward, Adsorption of gases in multimolecular layers, "Journal of the American Chemical Society", 60, 1938, pp. 309-319.
Brunauer 1945: Brunauer, Stephen, The adsorption of gases and vapors, Princeton (N.J.), Princeton University Press, 1945.
Derjaguin, Landau 1941: Derjaguin, Boris V. - Landau, Lev D., Theory of the stability of strongly charged lyphobic sols and of the adhesion of strongly charged particles in solutions of electrolytes, "Acta physico-chimica" (URSS), 14, 1941, pp. 633-662.
Draves 1939: Draves, Carl Z., Evaluation of wetting agents-official method, "American Dyestuff reporter", 28, 1939, pp. 425-428.
Falbe 1986: Falbe, Jürgen, Surfactants in consumer products, Berlin, Springer, 1986.
Fridrikhsberg 1986: Fridrikhsberg, Dmitri A., A course in colloid chemistry, Moscow, Mir, 1986.
Fuchs 1934: Fuchs, Nikolaj, Über die Stabilität und Aufladung der Aerosole, ‟Zeitschrift für Physik", 89, 1934, pp. 736-743.
Giles 1960: Giles, Charles H. e altri, A system of classification of solution adsorption isotherms, and its use in diagnosis of adsorption mechanism and in the measurement of specific surface areas of solids, "Journal of the Chemical Society", 1960, pp. 3973-3993.
Hamaker 1937: Hamaker, H.C., The London-van der Waals attraction between spherical particles, "Physica", 4, 1937, pp. 1058-1072.
Hirtzel, Rajagopalan 1985: Hirtzel, Cynthia S. - Rajagopalan, Raj, Colloidal phenomena, Park Ridge (N.J.), Noyes, 1985.
Langmuir 1918: Langmuir, Irving, The adsorption of gases on plane surface of glass, mica and platinum, "Journal of the American Chemical Society", 40, 1918, pp. 1361-1403.
Myers 1988: Myers, Drew, Surfactant science and technology, New York, VCH, 1988.
Parfitt 1969: Parfitt, Geoffrey D., Dispersion of powders in liquids, Amsterdam, Elsevier, 1969.
Santacesaria, Visca 1985: Chimica fisica dei colloidi e delle interfasi, a cura di Elio Santacesaria, Mario Visca, Milano, CLUP, 1985.
Schick, Fowkes 1991: Schick, Martin J. - Fowkes, Frederick M., in: Alkylene oxides and their polymers, edited by Frederick E. Bailey, Joseph V. Koleske, New York, Dekker, 1991.
Shaw 1986: Shaw, Duncan J., Introduction to colloid and surface chemistry, London, Butterworths, 1986.
Shinoda, Arai 1965: Shinoda, Kozo - Arai, Haruhiko, Solubility of nonionic surface-active agents in hydrocarbons, "Journal of colloid science", 20, 1965, pp. 93-97.
Shinoda, Saito 1969: Shinoda, Kozo - Saito, Hiroyuki, The stability of O/W type emulsions as a function of temperature and the HLB of emulsifiers, "Journal of colloid and interface science", 30, 1969, pp. 258-263.
Smoluchowski 1917: Smoluchowski, Marian, Versuch einer mathematischen Theorie der kolloidalen Lösungen, ‟Zeitschrift für physikalische Chemie", 92, 1917, pp. 129-168.
Verwey, Overbeek 1948: Verwey, Evert J.W. - Overbeek, Jan Th.G., Theory of the stability of lyphobic colloids, New York, Elsevier, 1948.
Vold, Vold 1983: Vold, Robert D. - Vold, Marjorie J., Colloid and interface chemistry, Reading (Mass.)-London, Addison-Wesley, 1983.
Ward, Du Reau 1993: Ward, A.J.I. - du Reau, Charles, Surfactant association in nonaqueous media, in: Surface and colloid science, edited by Egon Matijevic, New York-London, Plenum, 1993.