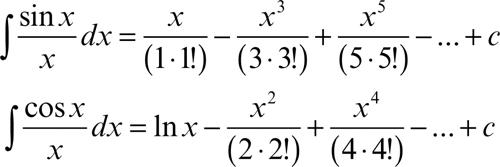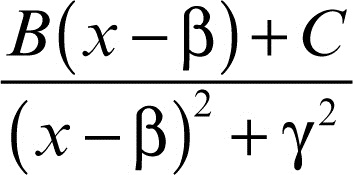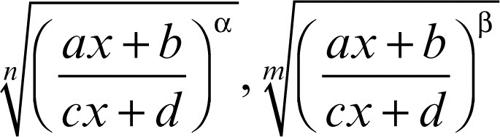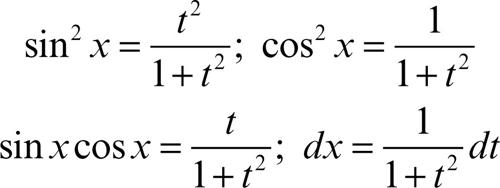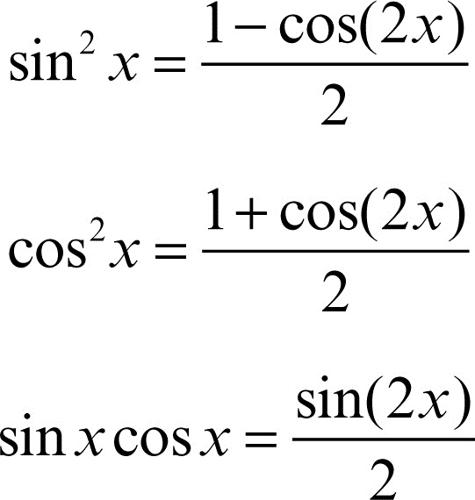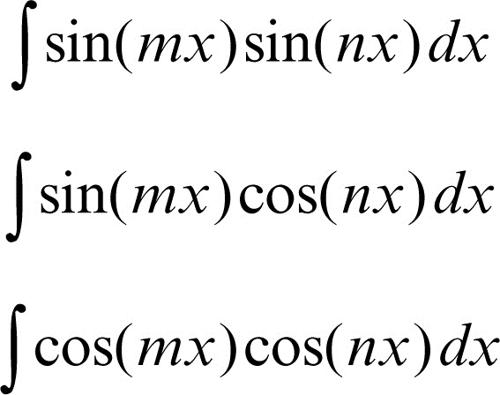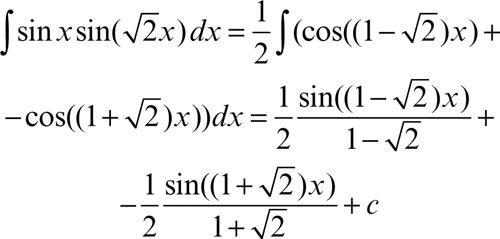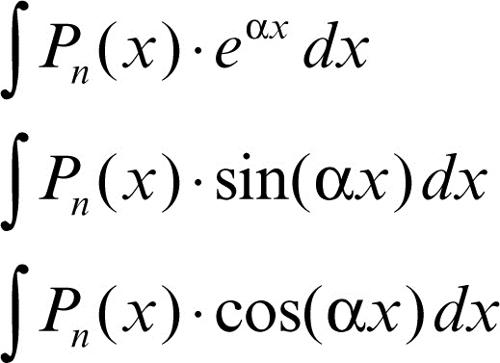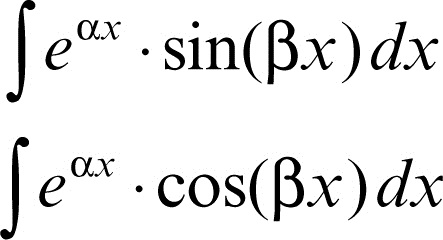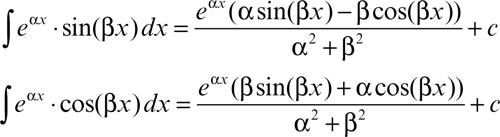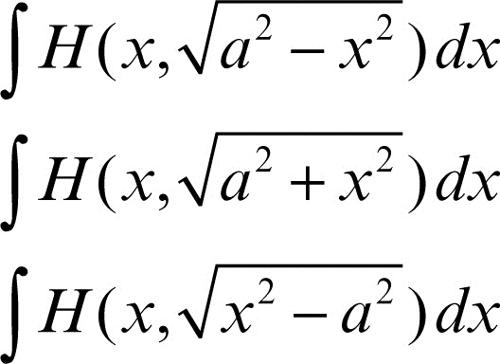integrazione
integrazione
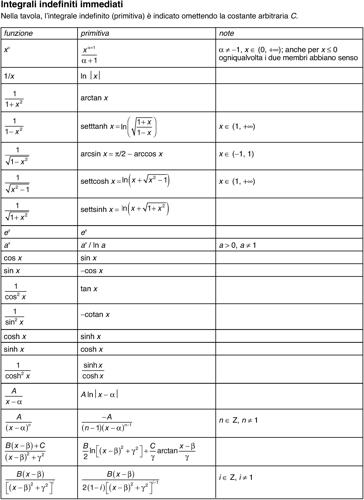
integrazione termine con cui si indica il calcolo di un → integrale: l’integrazione di una funzione consiste nella ricerca delle sue primitive. Il termine è usato anche per indicare la risoluzione di un’→ equazione differenziale. La ricerca delle primitive è immediata solo per alcune funzioni quale procedimento inverso della derivazione; in tali casi si parla di integrali (indefiniti) immediati (si veda la relativa tavola con i principali tra essi). Per altri casi, si utilizzano invece procedimenti fondati sulle proprietà dell’integrale detti appunto metodi di integrazione. Tra essi il metodo più elementare è quello per somma, che riporta il calcolo dell’integrale della somma di due funzioni alla somma degli integrali delle due funzioni, in base alla proprietà additiva dell’integrale:
Per i due principali metodi di integrazione, rispettivamente per parti e per sostituzione, si rinvia ai relativi lemmi (→ integrazione per parti; → integrazione per sostituzione). Oltre a tali metodi, si impiega anche il metodo di integrazione per serie quando la funzione integranda è rappresentata come somma di una serie uniformemente convergente. Per esempio:
Integrazione di funzioni razionali
Tutte le funzioni razionali sono dotate di primitive esprimibili in termini finiti mediante le funzioni elementari. Nel caso di funzione razionale intera (funzioni polinomiali), l’integrazione è immediatamente riconducibile all’applicazione delle proprietà dell’integrale. La determinazione di una primitiva di una funzione razionale fratta si riconduce invece alla decomposizione in fattori del denominatore. Tale decomposizione è sempre teoricamente possibile, in virtù del teorema fondamentale dell’algebra, ma nella pratica è impossibile in forma analitica per denominatori generici di grado maggiore di 4. In tal caso, comunque, adeguati metodi numerici consentono sempre la soluzione del problema.
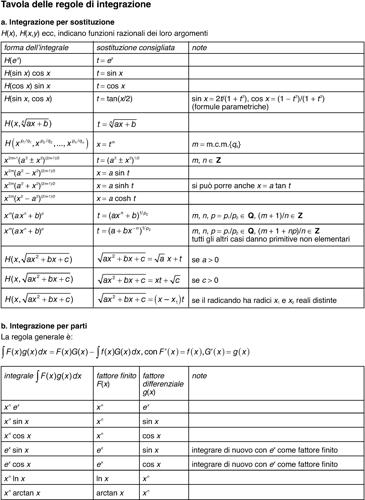
Si consideri la funzione razionale ƒ(x) = p(x)/q(x) di cui si voglia determinare una primitiva F(x). Non è restrittivo supporre che il grado di p sia minore di quello di q, perché a tal caso ci si può ridurre con una divisione tra i polinomi. Si descrive qui in dettaglio il procedimento nel caso di denominatore di secondo grado, lasciando il caso generale alle tavole delle regole d’integrazione (si vedano le tavole). Se la funzione q(x) = ax 2 + bx + c ha due radici reali distinte α e β, risulta q(x) = a(x − α)(x − β); si procede allora a determinare i due coefficienti indeterminati A e B per cui valga l’identità
Moltiplicando i due membri per q(x) e semplificando si ha p(x) = Aa(x − β) + Ba(x − α); per il principio di identità dei polinomi, basta imporre che i due membri (entrambi di grado minore di 2) coincidano per i valori x = α e x = β. Si ha subito, sostituendo tali valori: A = p(α)/[a(α − β)], B = p(β)/[a(β − α)]. Una volta trovati A e B, si ha (a meno di una costante arbitraria che si omette per evitare confusione con le costanti A e B)
Se q(x) ha una radice α doppia, q(x) = a(x − α)2, e si porrà
da cui ancora p(x) = Aa(x − α) + Ba.
Ponendo in questa x = α si trova B = p(α)/a; per determinare A basta sostituire un altro valore qualsiasi di x, o, più semplicemente, confrontare i coefficienti di x nei due membri (se p(x) = mx + n, si ha A = m /a). La primitiva è allora
Infine, nel caso di radici complesse coniugate β ± iγ, si scriverà ƒ(x) nella forma
e si avrà
Integrazione di funzioni irrazionali
Per questa classe di funzioni è spesso, ma non sempre, possibile individuare un’opportuna sostituzione che riconduca il problema a quello dell’integrazione di una funzione razionale più facilmente trattabile. In particolare:
• per funzioni del tipo
con m, n ∈ N e maggiori di 1; α, β ∈ Z; a, b ∈ R. Funzioni di questo tipo si possono integrare con la sostituzione ax + b = t p con p minimo comune multiplo tra gli indici delle radici;
• il precedente tipo di sostituzione è efficace anche se nella funzione compaiono radici del tipo
con m, n ∈ N e maggiori di 1; α, β ∈ Z; a, b, c, d ∈ R tali che ad − cb ≠ 0 (altrimenti la funzione si ridurrebbe a una costante). In questo caso la sostituzione è
con p minimo comune multiplo tra gli indici delle radici;
• per funzioni del tipo
si possono utilizzare diverse sostituzioni dette sostituzioni di Eulero:
a) se a > 0, si può porre
dove il segno davanti a √(a) può essere indifferentemente positivo o negativo. Un caso particolare di integrale di questa forma è l’integrale
Posto
elevando al quadrato entrambi i membri si ha
e
e sostituendo nell’integrale:
poiché
si ottiene:
b) se c > 0, si può porre
dove il segno davanti a √(c) può essere indifferentemente positivo o negativo. Scegliendo il segno positivo, elevando al quadrato entrambi i membri ed esplicitando x (scartando la soluzione x = 0), si ottiene x come funzione razionale di t;
c) se il trinomio ax 2 + bx + c ha radici reali e distinte x1 e x2, si può porre
Elevando al quadrato entrambi i membri, si ottiene infatti
da cui si esprime x come funzione razionale di t:
Integrazione di funzioni goniometriche
I tipi più frequenti di integrazione di funzioni goniometriche possono essere considerati i seguenti:
• integrale di una funzione razionale in sinx e cosx, del tipo H(sinx, cosx); si integra con la sostituzione t = tan(x/2), da cui dx = 2/(1 + t 2)dt. Si trasforma così la funzione in una funzione algebrica razionale, integrabile con i consueti metodi di integrazione; per esempio:
con la sostituzione
si ottiene tan(x /2) + c;
• integrale di una funzione del tipo
con H funzione razionale o irrazionale; si integra con la sostituzione tanx = t, da cui:
Per esempio:
con le sostituzioni indicate diventa:
• integrale del tipo
facilmente risolvibile se almeno uno dei due esponenti, n o m, è dispari; se n è dispari si esegue la sostituzione cosx = t; se m è dispari si sostituisce invece sinx = t. Se m e n sono ambedue pari e positivi, si integra dopo aver trasformato la funzione con le formule ricavate dalle formule di duplicazione
Per esempio:
con le sostituzioni indicate diviene
da cui si ottiene
• integrali del tipo
si calcolano trasformandoli attraverso le formule di → Werner. Per esempio:
Integrazione di alcune classi particolari di funzioni
Per l’integrazione di altri tipi di funzioni si utilizzano opportune sostituzioni o successive integrazioni per parti. Per esempio:
• gli integrali del tipo:
con Pn(x) polinomio di grado n e α ∈ R si integrano applicando n volte il metodo di integrazione per parti, integrando ogni volta il fattore funzione trascendente: eαx, sin(αx), cos(αx). A ogni integrazione si ottiene un nuovo integrale in cui il grado del polinomio diminuisce di 1;
• gli integrali del tipo:
con α, β ∈ R, si integrano per parti, assumendo come fattore da integrare sin(βx) o cos(βx). È facile dimostrare che risulta:
• gli integrali del tipo:
si possono integrare con le rispettive sostituzioni: x = a ⋅ sint, x = a ⋅ tant, x = asect = a/cost
• gli integrali del tipo:
con m, n, p ∈ Q e a, b ∈ R si possono risolvere solo nei tre casi seguenti:
a) se p ∈ Z, si effettua la sostituzione x = t k con k minimo comune multiplo dei denominatori di m e n;
b) se (n + 1)/m ∈ Z, si sostituisce axm + b = t k dove k è il denominatore di p;
c) se ((n + 1)/m + p) ∈ Z, si sostituisce
dove k è il denominatore di p.
