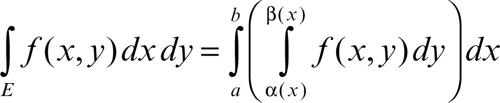integrazione numerica

integrazione numerica

integrazione numerica insieme dei metodi numerici per il calcolo approssimato di un integrale definito. Nel caso di funzioni di una variabile esistono metodi numerici, anche detti formule di quadratura, che si fondano sul calcolo approssimato dell’integrale mediante una combinazione lineare del tipo: I_n+1 = a₀ƒ(x₀) + ... + a_nƒ(x_n) dove i punti x_i tali che a ≤ x₀ < x₁ < ... < x_n ≤ b sono detti nodi e i numeri a_i sono detti pesi (o coefficienti). Si dice che una formula ha grado di precisione m se fornisce esattamente l’integrale di ogni polinomio di grado al più m. Nella famiglia delle formule di quadratura si possono distinguere le seguenti categorie:

• le formule di quadratura interpolatorie: si fondano in particolare sull’integrazione di un polinomio che interpola la funzione integranda su n + 1 nodi (→ interpolazione). Se i nodi sono scelti equidistanti, x_j = x₀ + jh, con j = 0, ..., n, e h costante, si ottengono le formule di Newton-Cotes (dai nomi di I. Newton e del matematico inglese R. Cotes) di tipo chiuso, ovvero di tipo aperto, a seconda che gli estremi a e b siano, oppure non siano, essi stessi nodi: si dimostra che tali formule hanno grado di precisione n se n è dispari ovvero n + 1 se n è pari;

• le formule di quadratura composte si ottengono suddividendo preliminarmente l’intervallo di integrazione in N parti uguali, ciascuna delle quali chiamata passo d’integrazione, e quindi applicando una stessa formula di approssimazione su ciascuna di esse; per tale ragione queste formule risultano molto convenienti nel calcolo automatico, in quanto da esse è possibile costruire semplici algoritmi iterativi di risoluzione.

Se i nodi sono le radici di un opportuno → polinomio ortogonale, si ottengono le formule di quadratura gaussiana che con n + 1 nodi hanno grado di precisione 2_n + 1. I diversi metodi numerici per il calcolo degli integrali definiti operano suddividendo l’intervallo di integrazione in N sottointervalli e approssimando in ciascuno di essi il valore dell’integrale con una determinata procedura geometrica: approssimando l’integrale con un insieme di rettangoli aventi ciascuno come base il corrispondente sottointervallo e come altezza il valore della funzione a un estremo di essi (→ rettangoli, metodo dei); approssimando l’andamento della funzione con segmenti tangenti alla curva stessa (→ tangenti, metodo delle); congiungendo i punti della funzione ƒ(x) agli estremi del sottointervallo e calcolando l’area dei trapezi che da essi si formano (→ trapezi, metodo dei); approssimando l’andamento della funzione con segmenti parabolici (→ Cavalieri- Simpson, metodo di). Mentre i primi tre metodi approssimano linearmente l’andamento della funzione in ciascun sottointervallo, risultando quindi metodi del primo ordine, l’ultimo è del secondo ordine perché l’approssimazione è realizzata mediante un arco di parabola. Oltre che per il calcolo diretto di integrali definiti, le tecniche di integrazione numerica vengono utilizzate per il calcolo della soluzione approssimata delle equazioni differenziali (→ equazione differenziale, metodo numerico per la risoluzione di una; → Eulero, metodo di (per la risoluzione di una equazione differenziale)).

Nel caso delle ƒunzioni di più variabili non vi è alcun procedimento simile a quello dedotto dal teorema fondamentale del calcolo integrale. I metodi di integrazione più usati fanno ricorso a formule di riduzione che consentono di ricondurre un’integrazione multipla a una sequenza di integrazioni semplici, e a cambiamenti di variabile. Nel caso di una funzione di due variabili, se il dominio di integrazione E è l’insieme formato dai punti del piano Oxy di ascissa x contenuta in un intervallo [a, b] e ordinata y contenuta, per ogni x, in un intervallo α(x) ≤ y ≤ β(x), con α(x) e β(x) funzioni continue in [a, b] (si parla di dominio normale rispetto all’asse x) si ha

dove al secondo membro si calcola dapprima l’integrale entro parentesi, ottenendo una funzione di x che va poi integrata tra a e b. Formule analoghe valgono per funzioni di più di due variabili. Un cambiamento di coordinate, del tipo x = φ(u, v), y = ψ(u, v), permette di trasformare l’integrale

dove E′ è l’insieme di definizione di φ e ψ e |J(u, v)| è il valore assoluto del determinante della → matrice jacobiana di φ e ψ rispetto a u e v; in particolare, per le coordinate polari, è J = ρ². Sussistono formule analoghe per gli integrali tripli: J = ρ²senθ per le coordinate polari e J = ρ per le coordinate cilindriche.

Il calcolo numerico degli integrali multipli presenta difficoltà assai rilevanti, legate al fatto che la teoria dell’interpolazione e quella dei polinomi ortogonali in Rⁿ sono complesse e rendono ardua l’estensione a più dimensioni dei risultati disponibili per l’integrazione semplice.