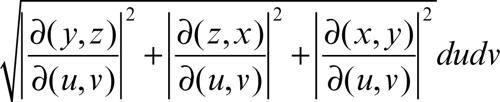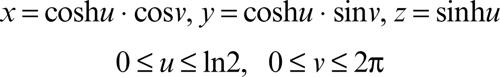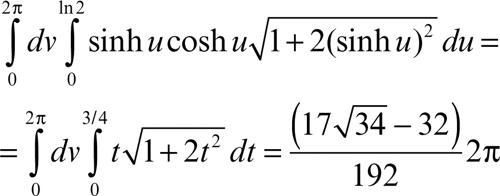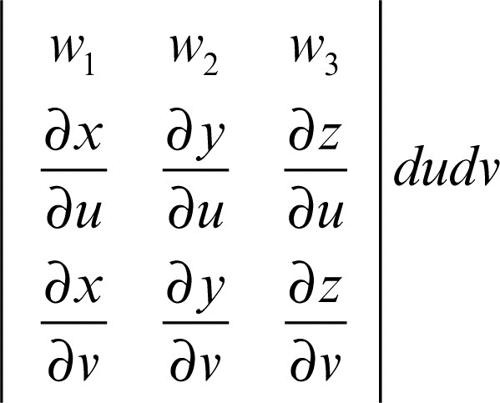integrale superficiale

integrale superficiale

integrale superficiale o integrale di superficie, integrale il cui dominio è una superficie S. Gli integrali di superficie sono di due tipi: quelli dipendenti solo dall’elemento di area dS, come il baricentro, e quelli che richiedono un orientamento della superficie, come il flusso.

Nel primo caso, se S è una superficie regolare, rappresentata dalle equazioni parametriche

l’elemento d’area dS è dato da

espressione che si riduce a

nel caso di superficie scritta nella forma cartesiana z = z(x, y). Se ƒ(x, y, z) è una funzione continua su S, l’integrale di ƒ su S

si esprime mediante un integrale esteso al dominio base T. Per esempio, sia S il tronco dell’iperboloide di rotazione x ² + y ² = z ² + 1 delimitato dai piani z = 0 e z = 5/4. Le sue equazioni parametriche sono

per cui:

L’integrale

allora si esprime come

che con le formule di riduzione (→ integrale multiplo) diviene:

Nel caso del flusso, si considera un integrale del tipo

dove w = w(x, y, z) è un vettore continuo su S e n la normale esterna alla superficie. In questo caso si può evitare il calcolo di dS perché il prodotto scalare w ⋅ ndS si esprime direttamente con il determinante

Per esempio, il flusso del vettore w = x ²i + yj + zk attraverso la superficie precedente vale