integrale singolare

integrale singolare

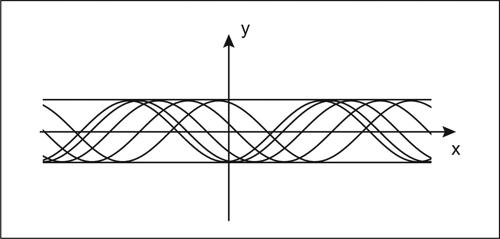
integrale singolare di una equazione differenziale in forma non normale F(x, y, y′ ) = 0, è una soluzione che soddisfa anche l’equazione F_y′ (x, y, y′ ) = 0. Quando F_y′ (x, y, y′ ) ≠ 0, è possibile infatti risolvere l’equazione rispetto a y′, trasformandola in un’equazione in forma normale, per cui vale il teorema di esistenza e unicità. La condizione F_y′ (x, y, y′ ) = 0 corrisponde quindi ai casi in cui, presumibilmente, tale teorema non sussiste, e quindi in cui un problema di → Cauchy ammette più di una soluzione. Tipico è il caso degli inviluppi di una famiglia di soluzioni di un’equazione differenziale: essi infatti soddisfano la medesima equazione, e ne sono integrali singolari. Per esempio, l’equazione differenziale y ² + y ′ ² − 1 = 0 ammette come integrale generale la famiglia di sinusoidi traslate y = sin(x + C), ma anche le rette y = ±1, che ne sono gli inviluppi. Tali rette soddisfano anche l’equazione differenziale 2y′ = 0, ottenuta derivando parzialmente l’equazione data rispetto a y′, e sono pertanto integrali singolari.