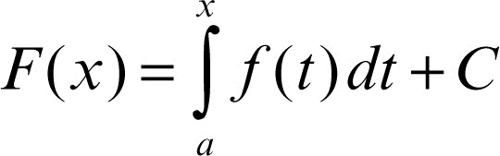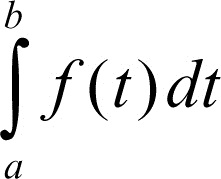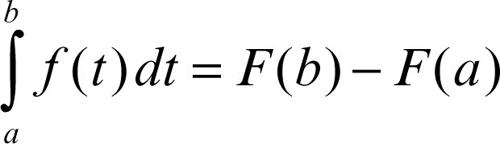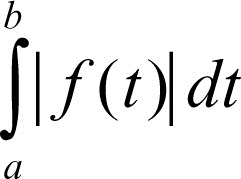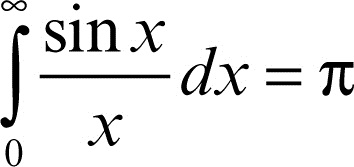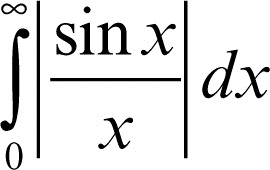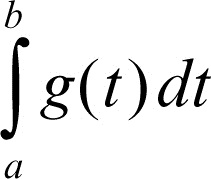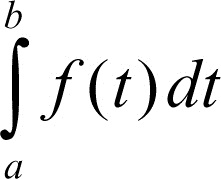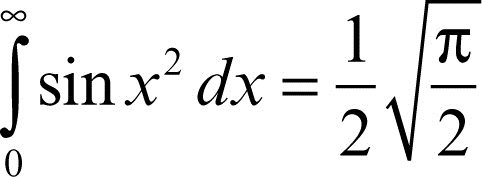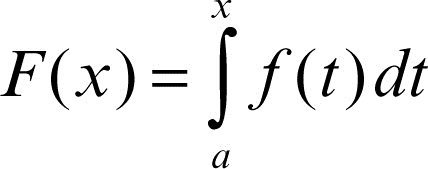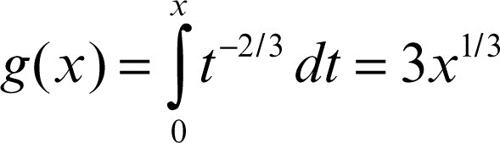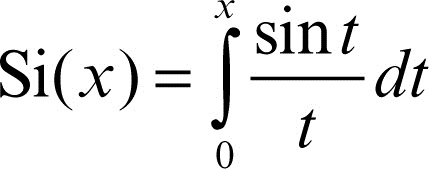integrale improprio

integrale improprio

integrale improprio estensione del concetto di integrale definito a funzioni non continue o su intervalli non limitati. Nella teoria dell’integrazione secondo Cauchy, è richiesto che la funzione integranda ƒ(x) sia continua in un intervallo chiuso e limitato [a, b]. Se ƒ(x) è continua solamente nell’intervallo [a, b), o se b = +∞, è naturale considerare una funzione integrale

che è sicuramente anch’essa continua in [a, b), e calcolarne il limite per x → b⁻ (che si legge «limite per x che tende a b da sinistra»). Nel caso in cui tale limite esista finito, si dice che ƒ(x) è integrabile in senso improprio o generalizzato nell’intervallo [a, b], o in un intorno sinistro di b, e si pone

Da qui l’aggettivo improprio o generalizzato che si attribuisce a tale integrale. Si dice pure che l’integrale

converge. La primitiva F(x) è allora continua in tutto [a, b], e risulta

Se invece il limite è infinito si dice che l’integrale diverge; se il limite non esiste, si dice che l’integrale è oscillante. Se l’integrale

converge, si dice che la funzione ƒ è assolutamente integrabile. Una funzione può essere integrabile senza essere assolutamente integrabile: per esempio,

mentre

diverge. Condizioni sufficienti per la convergenza di un integrale si ottengono mediante il criterio del confronto: se |ƒ(x)| ≤ g(x) in [a, b], e se

converge, allora anche

converge (assolutamente). In particolare, se per x → b⁻ risulta ƒ(x) ∼ g(x), e se g è assolutamente integrabile, anche ƒ lo è. Se b < +∞, si considerano le funzioni g(x) = 1/|x − b|^α, il cui integrale converge per α < 1 e diverge per α > 1. Se ne deduce che è integrabile in un intorno sinistro di b ogni funzione che sia infinita di ordine α < 1 (si noti che non basta che la funzione sia infinita di ordine minore o uguale a 1: per esempio, ƒ(x) = 1/(xln|x|) non è integrabile in un intorno dell’origine). Se invece b = +∞, le funzioni g(x) = 1/x^α risultano integrabili per α > 1, per cui è integrabile in un intorno di +∞ ogni funzione che sia infinitesima di ordine α > 1 rispetto a 1/x. Tali criteri sono però sufficienti (e non necessari): per esempio,

e la funzione integranda non è neppure infinitesima per x → ∞.

Come per le serie, non esiste una funzione il cui integrale converga o diverga più lentamente di tutte le altre. Per esempio, le funzioni 1/x, 1/(xlnx), 1/(xlnxlnlnx) ecc., hanno tutte integrale divergente in un intorno di +∞, e ciascuna è infinitesima di ordine maggiore delle precedenti.

In modo analogo si ragiona per una funzione continua in (a, b] (ossia nel caso che l’intervallo sia aperto a sinistra), con a finito o a = −∞. Se poi ƒ(x) è continua in (a, b), si considerano separatamente i due estremi. Infine, se esistono punti di discontinuità d_k interni all’intervallo (a, b), si deve valutare l’integrabilità di ƒ negli intorni sinistro e destro di ciascuno di essi, e ogni condizione è indipendente dalle altre. Per esempio, la funzione e^x+1/x è integrabile nell’intorno di −∞ e in 0⁻, e dunque è integrabile in (−∞, 0], ma non in 0⁺ e in +∞.

Tra i più importanti integrali impropri che non possono essere calcolati in modo elementare si segnalano

La funzione integrale

è continua in ogni intervallo di integrabilità di ƒ(x), e derivabile dove ƒ è continua, mentre nei punti di discontinuità F(x) presenta:

• un punto angoloso dove ƒ(x) ha un salto: per esempio, se ƒ(x) = sgn(x) è F(x) = |x|;

• una cuspide o un flesso verticale, a seconda dei segni, dove ƒ(x) ha un asintoto verticale: per esempio, la funzione

ha una cuspide, mentre la funzione

ha un flesso verticale;

• un punto di regolarità dove ƒ(x) ha una discontinuità eliminabile: per esempio, la funzione integralseno

ammette derivata Si′(0) = 1.

Se invece in un estremo ƒ(x) non è integrabile, F(x) non ammette limite finito (ha un asintoto verticale se ƒ(x) ha segno costante).