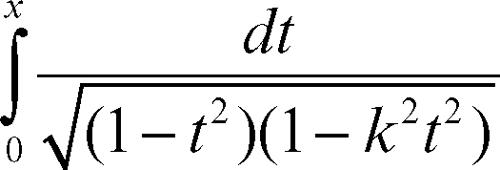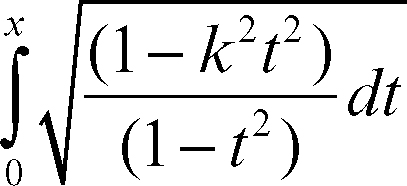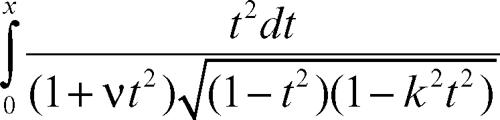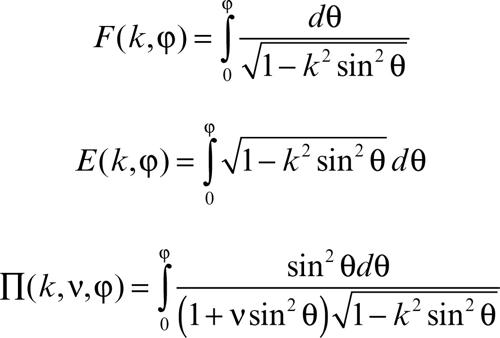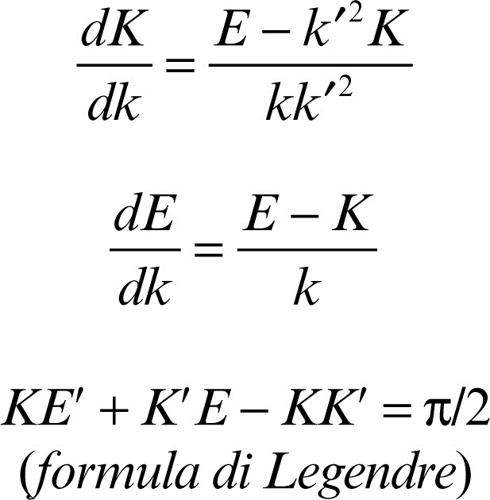integrale ellittico

integrale ellittico

integrale ellittico integrale di una funzione razionale di una variabile t e della radice quadrata di un polinomio di terzo o quarto grado in t. Con opportune sostituzioni, è sempre possibile ridursi a una delle seguenti tre forme canoniche:

dette rispettivamente integrale ellittico di prima, seconda e terza specie. Con la sostituzione

questi integrali si trasformano in

I valori

sono i corrispondenti integrali ellittici completi. Posto

valgono le relazioni

Il nome di integrale ellittico deriva dal problema della rettificazione dell’ellisse: infatti una ellisse di semiassi a e b, e quindi di eccentricità e = b /a, ha lunghezza 4aE(e, π/2), e in generale l’arco compreso tra il vertice (0, b) e il punto di ascissa x = acosφ dell’ellisse x ²/a² + y ²/b² = 1 ha lunghezza 4aE(k, φ) (→ funzione ellittica).