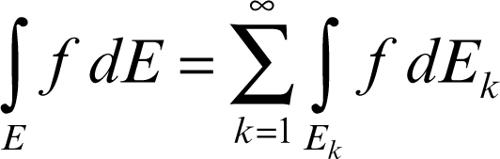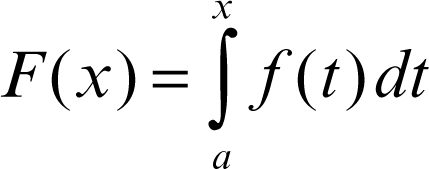Lebesgue, integrale di
Lebesgue, integrale di
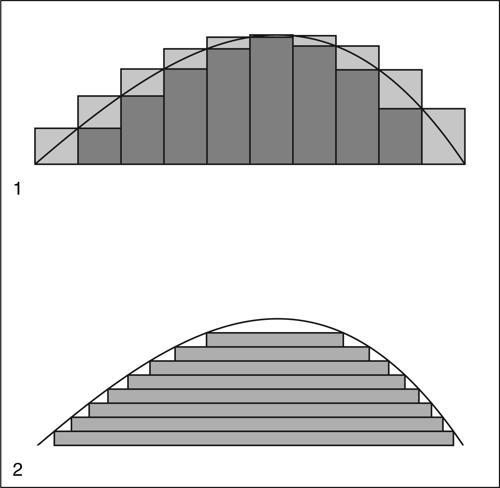
Lebesgue, integrale di in analisi, definizione di integrale di una funzione rispetto alla misura di Lebesgue, che rappresenta un cambio di prospettiva rispetto a quella secondo Cauchy-Riemann (→ Riemann, integrale di). Mentre infatti, classicamente, per costruire le somme integrali si suddivide il dominio in parti di lunghezza (diametro) minore di δ, in ciascuna delle quali si approssima la funzione da integrare, e si rende poi sempre più fine la decomposizione del dominio facendo tendere δ a zero, nell’ottica di Lebesgue si suddivide il codominio in intervalli di lunghezza minore di ε e si approssima la funzione con una funzione a livelli (→ Lebesgue, funzione misurabile secondo), per ciascuno dei quali la controimmagine è un insieme misurabile, ma di struttura a priori complicata, e si fa quindi tendere ε a zero.
Se ƒ(x) è una funzione misurabile in un insieme E di misura finita m(E) ed è una funzione a livelli, che assume i valori {λn} negli insiemi Sn, l’integrale di ƒ in E si definisce ponendo
nell’ipotesi che tale serie sia assolutamente convergente. Tale ipotesi garantisce che l’ordine con cui sono presi gli addendi sia irrilevante (→ Riemann-Dini, teorema di).
Se ƒ(x) è una funzione misurabile, è possibile approssimarla con un errore minore o uguale a ε, scelto piccolo a piacere, mediante una funzione a livelli, purché tali livelli differiscano per non più di ε (basta assumere, per esempio, λn = nε, con n intero relativo). Si dimostra che per ε → 0 gli integrali di tali approssimanti ammettono un limite finito, che viene detto integrale di Lebesgue di ƒ. Il simbolo rimane sempre
o altre scritture analogamente utilizzate per l’integrale. La definizione si estende poi al caso di insiemi di misura infinita.
Tutte le proprietà elementari dell’integrale rimangono valide, ma nel caso dell’integrale di Lebesgue una funzione risulta integrabile se e solo se è assolutamente integrabile. Perciò gli integrali impropri non assolutamente convergenti corrispondono a funzioni non integrabili nel senso di Lebesgue. A parte questo fatto, la nozione di integrale di Lebesgue amplia moltissimo la classe delle funzioni integrabili e soprattutto garantisce alcuni teoremi di grande rilevanza e di portata assai ampia:
1) additività numerabile: se
con m(Ei ∩ Ej) = 0 allora ∀i, j, risulta
2) convergenza dominata di Lebesgue: se
q.o. in E ed esiste g(x) integrabile in E, tale che |ƒn(x)| ≤ g(x) in E, allora
3) convergenza monotona di Beppo Levi: se
q.o. in E, con {ƒn(x)} non decrescente, e se la successione degli integrali
è limitata, allora ƒ(x) risulta integrabile e
Tale proprietà deve il nome al matematico italiano B. Levi.
4) teorema di Radon-Nikodým: se μ è una misura (anche complessa) tale che μ(E) = 0 se m(E) = 0, allora esiste una funzione integrabile ƒ tale che, per ogni E misurabile, si abbia
Questo teorema è stato dimostrato nel 1913 dal matematico austriaco J. Radon e nel 1930 generalizzato dal matematico statunitense di origine polacca O.M. Nikodým.
Per funzioni di una variabile, il teorema fondamentale del calcolo integrale assume la forma: se ƒ(x) è integrabile secondo Lebesgue in [a, b], la funzione integrale
è assolutamente continua in [a, b], è derivabile q.o. e risulta q.o. F′ (x) = ƒ(x). Per le formule di riduzione degli integrali multipli, si vedano i teoremi di → Fubini e di → Tonelli.
