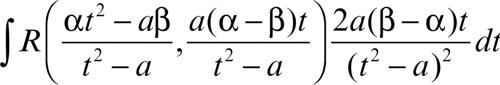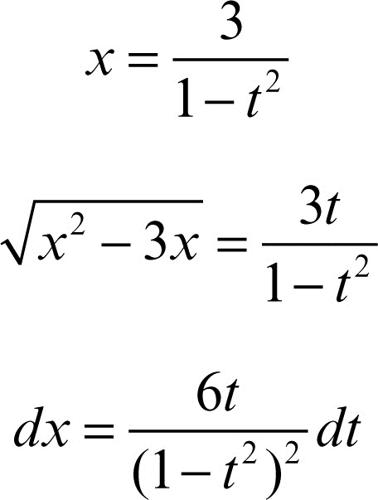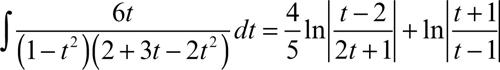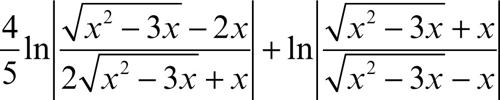integrale abeliano
integrale abeliano
integrale abeliano integrale di una funzione del tipo
dove R(x, y) è una funzione razionale dei suoi argomenti e Δ = b2 − 4ac ≠ 0 (per Δ = 0 la funzione è già razionale). Si dice che tale integrale appartiene alla conica di equazione y 2 = p(x) = ax 2 + bx + c e, poiché essa è una curva razionale, l’integrale è razionalizzabile. La sostituzione da utilizzare dipende dal radicando p(x):
• Se p(x) ammette radici reali, si può scrivere p(x) = a(x − α)(x − β). Posto allora y = (x − α)t (si tratta del fascio di rette passanti per il punto (α, 0) della conica), si ottiene, quadrando e risolvendo rispetto a x:
Da questa si deducono le espressioni del differenziale
e del radicale
in termini razionali di t. Pertanto l’integrale
si trasforma in
che è l’integrale di una funzione razionale (→ integrazione). Per esempio, dovendosi calcolare
si pone
da cui
L’integrale diviene dunque, semplificando,
da cui, ponendo
la primitiva cercata
• Se p(x) non ammette radici reali, si deve avere a > 0 affinché il radicando sia positivo, e la conica è un’iperbole. Si pone allora y = √(a)x + t (si tratta delle parallele a un asintoto) e di nuovo quadrando si ottiene
Il procedimento segue quindi le linee del caso precedente.