inscrivibilita

inscrivibilita

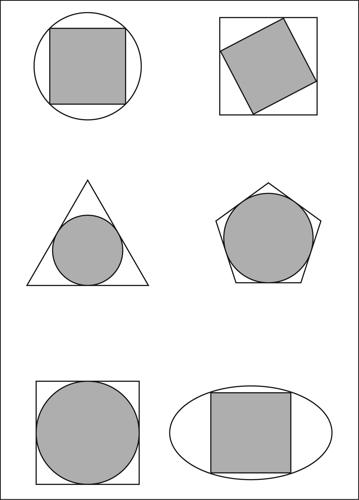
inscrivibilità in geometria, proprietà di una figura di poter essere inscritta, cioè tracciata internamente, a un’altra, rispettando alcune condizioni. La nozione è strettamente connessa a quella di → circoscrivibilità. Gli esempi più interessanti e più noti si riferiscono a poligoni e circonferenze. Per esempio, l’inscrivibilità di un poligono in una circonferenza equivale alla possibilità di tracciare tale poligono, detto poligono inscritto, in modo che tutti i suoi vertici giacciano sulla circonferenza. Tale possibilità dipende dalla natura e dalle proprietà del poligono. I triangoli, per esempio, sono tutti inscrivibili in una circonferenza, mentre i quadrilateri lo sono se e solo se hanno gli angoli opposti supplementari. In generale, un poligono è inscrivibile in una circonferenza se gli assi dei suoi lati concorrono tutti in uno stesso punto, che è il centro della circonferenza circoscritta. Da ciò discende che tutti i poligoni regolari sono inscrivibili in una circonferenza. Altro caso notevole riguarda l’inscrivibilità di una circonferenza in un poligono, cioè la possibilità di tracciare una circonferenza tangente internamente ai lati del poligono. In ogni triangolo può essere inscritta una circonferenza, mentre in un quadrilatero ciò è possibile se e solo se le somme delle lunghezze dei lati opposti sono uguali. In generale, una circonferenza risulta inscrivibile in un poligono se e solo se le bisettrici di quest’ultimo concorrono tutte in un medesimo punto, che è il centro della circonferenza inscritta. Da ciò segue che in ogni poligono regolare è inscrivibile una circonferenza. La nozione si può ulteriormente estendere a molteplici casi. Per esempio, si può stabilire l’inscrivibilità di un poligono in un poligono, di un poligono in un’ellisse, di un’ellisse in una circonferenza, di una circonferenza in un’ellisse ecc.