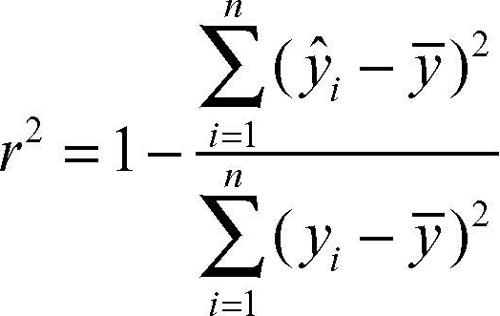determinazione, indice di

determinazione, indice di

determinazione, indice di in statistica, indice utilizzato nell’ambito dell’analisi della regressione per valutare la bontà d’adattamento dei dati a funzioni e, in particolare, a funzioni lineari. Potendo assumere un valore tra 0 e 1, rappresenta la proporzione della variazione delle variabili che è spiegata dalla legge funzionale scelta. È dato dalla seguente formula:

In essa ŷ_i = ƒ(x_i) rappresenta il valore teorico, corrispondente al dato x_i secondo la legge funzionale ƒ, ȳ il valore medio della variabile Y e y_i i valori osservati. Se la funzione si accosta in modo perfetto ai dati, cioè ŷ_i = y_i, per ogni i, allora la frazione assume il valore 0 e il coefficiente di determinazione il valore 1. È questo il caso di determinazione perfetta: tutte le variazioni delle variabili sono spiegate dal modello di regressione usato. Viceversa, più il coefficiente si avvicina a 0, meno adatta è la funzione a rappresentare la serie di dati statistici. L’indice si basa sulla scomposizione della devianza totale della variabile aleatoria y:

data dalla somma tra la devianza spiegata dalla regressione e la devianza residua.