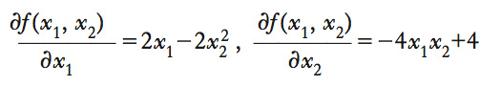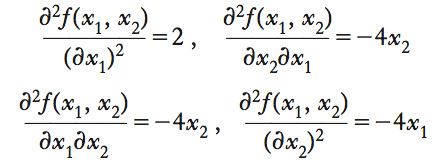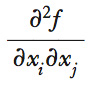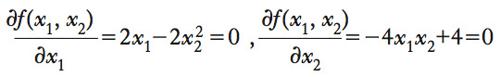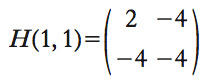hessiano

hessiano

Estensione del concetto di derivata seconda al caso di funzioni con due o più argomenti. Nel seguito viene considerato soltanto il caso di funzioni a valori reali. Per una funzione f(x₁,x₂) con due soli argomenti, è possibile definire 4 derivate seconde. Per es., se la funzione è: x²₁−2x₁x²₂+4x₂, si hanno due derivate prime

e 4 derivate seconde, ottenute prendendo le derivate parziali di ciascuna delle due derivate prime: formula

L’h. di f è la matrice H il cui elemento nella riga i-ma e nella colonna j-ma è uguale a formula

L’h. è funzione del punto (x₁,x₂) in cui le derivate sono calcolate ed è sempre simmetrico, in quanto le derivate seconde miste, se esistono, coincidono. Più in generale, per una funzione f(x₁,...,x_k), con k argomenti, l’h. è una matrice quadrata simmetrica di dimensione k. Per k=1, l’h. di f si riduce alla nozione di derivata seconda f′′. L’h. svolge un ruolo importante nelle applicazioni economiche ed econometriche, perché serve a verificare le condizioni del secondo ordine per un problema di ottimizzazione. Infatti, il punto (x₁^o,..., x_k^o) corrisponde a un punto di massimo (minimo) locale della funzione f(x₁^k,...,x_k^k), se l’h. di f valutato a quel punto è definito negativo (rispettivamente, definito positivo, ➔ positivo, definito). Così, per es., per la funzione f(x₁, x₂)=x₁²−2x₁x²₂+4x₂, risolvendo le due equazioni formula

si ottiene il punto critico (1,1) a cui corrisponde l’h. formula

che ha determinante (➔) negativo ed è definito negativo.