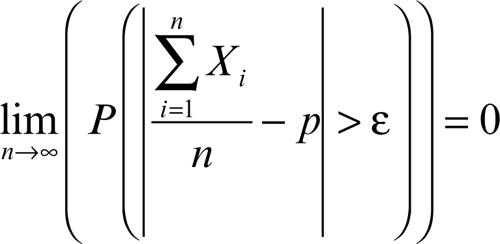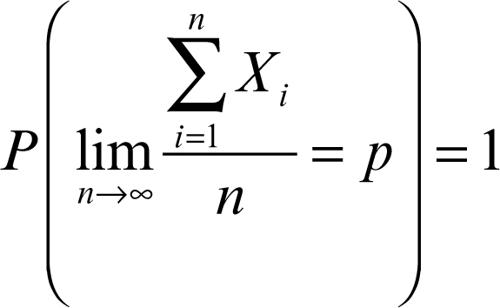grandi numeri, legge dei
grandi numeri, legge dei
grandi numeri, legge dei locuzione con cui, anche nel linguaggio comune, si esprime l’idea che in un “grande” numero di prove la frequenza relativa ƒ con cui si verifica un evento con probabilità p tende ad avvicinarsi a p. In teoria della probabilità, si distingue tra legge forte dei grandi numeri, dovuta a E. Borel (1900) e legge dei grandi numeri propriamente detta, talvolta detta legge debole dei grandi numeri per distinguerla dalla precedente e dovuta a Jakob Bernoulli (1713).
Legge debole dei grandi numeri
Stabilisce che se {Xn} è una successione di variabili aleatorie, indipendenti a due a due, con uguali distribuzione di probabilità e valore medio (o speranza matematica) E(Xi) = p, allora, per ogni ε > 0
Quindi, al tendere di n all’infinito, la probabilità P che lo scarto assoluto tra frequenza relativa e valore atteso sia maggiore di un qualunque valore positivo ε, “piccolo a piacere”, è nulla. In questo caso si dice che la successione converge in probabilità a p. In altre parole, se il numero delle prove effettuate è sufficientemente grande, è quasi certo che la frequenza relativa dei successi nelle n prove differirà molto poco dalla probabilità di successo nella singola prova.
Nel caso particolarmente importante in cui le variabili Xi sono variabili di → Bernoulli, la legge è anche detta teorema di Bernoulli (in probabilità). Numerosi fenomeni fisici confermano la legge dei grandi numeri. Per esempio, le molecole di un gas, con velocità e traiettorie aleatorie, quando sono in grande numero determinano sulle pareti di un recipiente una pressione pressoché costante.
Legge forte dei grandi numeri
Stabilisce che se {Xn} è una successione di variabili aleatorie, indipendenti a due a due, con uguali distribuzione di probabilità e valore medio (o speranza matematica) E(Xi) = p, allora
In questo caso si dice che la successione converge quasi certamente al valore costante p, dove con la locuzione «quasi certamente» si vuole intendere che la convergenza avviene per tutte le possibili determinazioni delle variabili, salvo per un numero di casi di misura nulla, ma tuttavia non impossibili.
Un caso particolarmente importante è quello in cui le variabili aleatorie Xi sono variabili di Bernoulli. Per esempio, ripetendo “numerose volte” e nelle stesse condizioni il lancio di una moneta equilibrata, uscirà “testa” oppure “croce” all’incirca nella metà dei casi, tanto quanto previsto dal valore di probabilità. Questa legge fornisce una possibile giustificazione della legge empirica del caso, secondo la quale la frequenza relativa di un evento tende a stabilizzarsi all’aumentare del numero delle prove. La legge dei grandi numeri non va tuttavia fraintesa, anche nella sua formulazione forte: essa non contraddice la valutazione di probabilità teorica di ogni singola realizzazione di un esperimento. Se per esempio, nei ripetuti 1000 lanci di una stessa moneta si è verificato un forte squilibrio di un evento rispetto all’altro (per esempio molte più “teste” che “croci”) non si deve pensare che a questo punto il caso giochi a favore dell’evento svantaggiato, dovendo compensare, per così dire, quanto avvenuto: è più ragionevole pensare a una bizzarria del caso stesso (il verificarsi di un fenomeno puntuale di probabilità praticamente nulla) oppure a una alterazione della moneta stessa.
Dal punto di vista delle applicazioni statistiche, la legge dei grandi numeri assicura che la media campionaria, per un numero n di prove nel campione sufficientemente grande, è uno stimatore consistente (→ stima) della media di una popolazione.