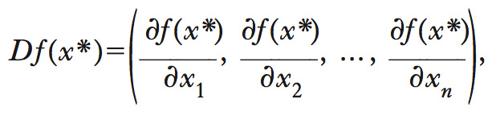gradiente

gradiente

Variazione per unità di lunghezza che una grandezza subisce da un punto all’altro dello spazio in una certa direzione. Data una funzione a n variabili f(x*₁, x*₂, ..., x*_n), il g. rappresenta un vettore le cui coordinate sono costituite dalle derivate della funzione nel punto x*:

dove D è l’operatore differenziale. Essenzialmente, il g. non differisce dalla derivata di una funzione in un punto. Sul piano geometrico, esso rappresenta la direzione in cui la funzione f(x*₁, x*₂, ..., x_n) cresce più rapidamente. Per es., se si prende una funzione di utilità, il suo g. valutato in un punto, per date quantità di beni, rappresenta la direzione in cui l’utilità cresce più velocemente ed è costituito dal vettore delle utilità marginali. Geometricamente, esso corrisponde al vettore perpendicolare alla tangente della curva d’indifferenza. Nella posizione di massima utilità, il g. della funzione di utilità e il vettore dei prezzi dei beni sono collineari, giacciono cioè sulla stessa linea. Dal punto di vista economico, ciò significa che le utilità marginali sono proporzionali ai prezzi.