geometria non euclidea

geometria non euclidea

geometria non euclidea geometria basata sulla negazione di uno o più postulati euclidei. La locuzione è tuttavia generalmente riservata, per le notevoli implicazioni storiche, filosofiche e matematiche, alle geometrie che si fondano sulla negazione del → quinto postulato. Questo, nella formulazione euclidea, stabilisce che se una retta t intersecando due rette r e s forma con esse angoli interni, da una stessa parte, minori di due retti, le due rette, indefinitamente prolungate, si incontrano da quella parte. Una formulazione equivalente è l’assioma della → parallela (che, nella sua formulazione corrente, afferma che per ogni retta r e per ogni punto P del piano esiste una sola retta s passante per P e parallela a r). Tra i postulati euclidei il quinto è sicuramente il più problematico e discusso. Viene introdotto nel primo libro degli Elementi nella proposizione 29 e pertanto tutto ciò che è stato dimostrato fino alla proposizione 28 è indipendente da esso. Per circa due millenni i matematici si sono chiesti se fosse possibile non doverlo enunciare come postulato, ma poterlo ricavare come teorema, basandosi sugli altri quattro postulati. Il motivo di tale ricerca stava nel fatto che il quinto postulato riguarda una proprietà all’infinito, l’intersecarsi o meno di due rette, e dunque una proprietà meno intuitiva delle altre postulate.

Nel corso dei secoli si sono succeduti innumerevoli tentativi di dimostrare il quinto postulato a partire dagli altri quattro. Si condivideva infatti con Euclide sia il suo carattere di “verità”, nel senso di corrispondenza con proprietà reali dello spazio fisico, sia il suo carattere di necessità nei confronti delle dimostrazioni dei teoremi successivi; strideva però il suo carattere di non evidenza. Tra i tentativi più significati vi fu quello di G. Saccheri che nel 1773, anno della sua morte, pubblicò l’Euclides ab omni naevo vindicatus (Euclide emendato da ogni difetto) in cui cercò di dimostrare il postulato attraverso un ragionamento per assurdo. Saccheri riteneva infatti che ammettendo come ipotesi la negazione del quinto postulato si potesse giungere a delle contraddizioni e quindi che per questa via lo si potesse ritenere dimostrato per assurdo. La sua argomentazione prende le mosse da un quadrilatero piano ABCD, con i lati AD e BC uguali e perpendicolari alla base AB.

Saccheri dimostra preliminarmente che i due angoli AD̂C e BĈD sono uguali. Per quanto riguarda l’ampiezza di tali angoli, senza fare ricorso al quinto postulato, egli considera i seguenti tre casi possibili:

• gli angoli A D̂C e BĈD sono retti: ipotesi dell’angolo retto;

• gli angoli AD̂C e BĈD sono ottusi: ipotesi dell’angolo ottuso;

• gli angoli AD̂C e BĈD sono acuti: ipotesi dell’angolo acuto.

Nella prima ipotesi (angolo retto) è possibile ricavare il teorema secondo cui la somma degli angoli interni di un triangolo è uguale a due retti, proposizione equivalente al quinto postulato.

Nella seconda ipotesi (angolo ottuso), poiché essa non è incompatibile con il quinto postulato, si possono ricavare tutti i teoremi da esso dipendenti, in particolare quello che afferma che la somma degli angoli interni di un quadrilatero è pari a quattro retti, mentre, in base all’ipotesi adottata, nel caso del quadrilatero ABCD tale somma è maggiore di quattro retti. Secondo Saccheri l’ipotesi dell’angolo ottuso entra in conflitto con sé stessa e quindi decade. In realtà egli non ha trovato incongruenza logica tra le premesse poste come base del processo deduttivo e le conseguenze che se ne deducono, ma solo incoerenza tra le conseguenze della sua premessa e quelle delle premesse euclidee.

Nella terza ipotesi (angolo acuto), infine, crede di aver trovato la contraddizione, ma commette l’errore di estendere all’infinito una proprietà valida al finito. Nell’ipotesi dell’angolo acuto egli giunge alla conclusione che non possono esistere rette asintotiche, cioè rette che si avvicinano sempre senza mai incontrarsi.

Saccheri ritiene così di aver dimostrato che sia l’ipotesi dell’angolo ottuso sia quella dell’angolo acuto portano a contraddizioni e che, pertanto, risulta valida solo l’ipotesi dell’angolo retto, dalla quale discende il quinto postulato. Nella sua trattazione, per quanto riguarda i triangoli, egli dimostra che:

• se si ammette l’ipotesi dell’angolo retto la somma degli angoli interni di un triangolo equivale a due retti;

• se si ammette l’ipotesi dell’angolo ottuso la somma degli angoli interni di un triangolo è minore di due retti;

• se si ammette l’ipotesi dell’angolo acuto la somma degli angoli interni di un triangolo è maggiore di due retti.

In tal modo Saccheri formulò e dimostrò una serie di teoremi diversi da quelli euclidei; l’importanza della sua opera consiste proprio in tale inconsapevole anticipazione di risultati non euclidei, appartenenti alle geometrie che oggi chiamiamo iperbolica ed ellittica. Egli tuttavia rimase “annebbiato” dal pregiudizio della validità assoluta dell’assioma della parallela e – senza rigorose motivazioni logiche – rifiutò l’ipotesi da lui stesso posta.

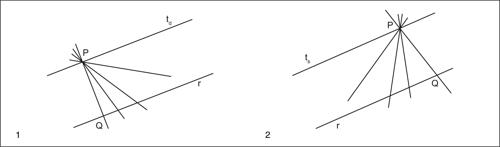
Fu soltanto nel xix secolo che il problema trovò una soluzione, ma in una direzione diversa da quella verso la quale si erano orientati tutti coloro che avevano tentato una dimostrazione del postulato della parallela. Il matematico russo N. Lobačevskij, partendo dall’idea che lo spazio fisico possa avere proprietà diverse da quelle che Euclide gli attribuiva, effettuò una ricostruzione della geometria assumendo come «enti primitivi» non più gli enti ideali (il punto e la retta), ma oggetti geometrici (quali i corpi solidi) più vicini all’esperienza sensibile. A partire da tali premesse, Lobačevskij negò il principio che la parallela a una retta per un punto a essa esterno sia unica. Se, infatti, non ci si lascia guidare dalle consuetudini e si imposta il discorso in termini strettamente razionali, si può osservare che la parallela a una retta, nel senso di Euclide, si ottiene in due modi diversi: data una retta per il punto P che intersechi una retta r in un punto Q, si può allontanare il punto di intersezione verso l’infinito da una parte (verso destra) o dall’altra (verso sinistra). Seguendo il ragionamento di Lobačevskij, nulla impedisce di pensare che tra la posizione della parallela destra t_d e quella della parallela sinistra t_s non vi siano altre rette che non intersecano la retta data. Date le piccole distanze che si è in grado di misurare, non è possibile apprezzare le differenze di ampiezza tra i diversi angoli che tali eventuali infinite parallele formerebbero con la retta r. Pertanto, nessuna effettiva misurazione potrebbe confermare oppure smentire tale diversa ipotesi. Lobačevskij non si limitò a discutere astrattamente la possibilità di costruire una geometria in cui una retta avesse più parallele per un punto esterno a essa, ma effettivamente dedusse una serie di teoremi da tali nuovi assiomi e costruì una vera e propria teoria geometrica diversa da quella di Euclide, ma logicamente coerente, priva di contraddizioni interne. Tra l’altro, nella geometria di Lobačevskij si dimostra che la somma degli angoli interni di un triangolo è uguale a π − k, in cui k, detto difetto, è un numero non negativo che dipende dalle dimensioni dei lati del triangolo e quanto più un triangolo è “grande” tanto maggiore è la sua differenza da un “normale” triangolo euclideo, in cui la somma degli angoli interni è uguale a un angolo piatto. Nell’ottica di Lobačevskij, perciò, tale geometria non contraddice la geometria euclidea, ma ne costituisce una generalizzazione. Infatti, rispetto alle grandezze piuttosto piccole che in genere si misurano, il difetto k è talmente piccolo da diventare trascurabile e diventa quindi corretta – per la classe di problemi che abitualmente si trattano – l’ipotesi euclidea.

Indipendentemente da Lobačevskij, nel 1832, un giovane ufficiale ungherese, J. Bolyai, pubblicò, in appendice a un libro di testo di matematica del padre Farkas, uno scritto dal titolo Appendix scientiam spatii absolute veram exhibens (Appendice che espone in maniera assoluta la vera scienza dello spazio). Anche in questo testo si faceva a meno dell’assioma della parallela e si costruiva una geometria coerente ma di tipo non euclideo. Il padre di Bolyai, che era un matematico, letto lo scritto del figlio, comunicò tali scoperte a C.F. Gauss, suo amico personale e una delle maggiori autorità matematiche del tempo. La reazione di Gauss fu sconsolante giacché così scrisse a Farkas Bolyai: «Se comincio col dirvi che non posso lodare l’opera di vostro figlio, non vi meravigliate perché sarebbe lo stesso che lodare me stesso: i risultati ai quali egli è arrivato coincidono quasi interamente con le mie riflessioni». In effetti, risulta documentata l’attenzione che Gauss aveva dedicato all’annoso argomento della dimostrabilità dell’assioma della parallela o della possibilità di rinunciarvi, ma non aveva pubblicato nulla su ciò per il timore di non essere compreso dai suoi contemporanei (per tema, come egli scrisse, «delle strida dei beoti»). Avuta questa risposta, Bolyai sospettò che Gauss volesse attribuirsi la primogenitura di tale scoperta e, mentre Lobačevskij continuò ad approfondire la nuova geometria, tanto da pubblicarne una trattazione organica nel 1840 (Nuovi princìpi della geometria), Bolyai smise definitivamente di occuparsi dell’argomento.

Ciò che interessa rilevare in tale vicenda è che nello stesso periodo, in tre paesi diversi e in modo indipendente gli uni dagli altri, tre matematici erano arrivati alle medesime conclusioni: la geometria di Euclide non aveva quei caratteri di necessità assoluta e di verità universale che fino ad allora le si erano attribuiti. Ciò metteva in crisi il sistema di idee e il quadro filosofico dell’epoca secondo i quali lo spazio euclideo non era soltanto la descrizione del mondo delle idee o del mondo ricavato dall’esperienza; la più grande autorità filosofica del Settecento, Immanuel Kant (1724-1804), fondava infatti la validità oggettiva della geometria sulla forma a priori dell’intuizione dello spazio e lo spazio, nella forma assoluta cui Euclide aveva dato rigore, era «la condizione della possibilità dei fenomeni».

I risultati delle ricerche matematiche cozzavano così con il sistema di interpretazione del mondo da parte della cultura dell’epoca e ciò spiega sia le reticenze di Gauss a comunicare in forma pubblica le sue riflessioni sia il fatto che, all’inizio, la geometria di Lobačevskij, pur destando stupore, venne vista più che altro come un curioso esercizio logico, nel quale ci si aspettava di trovare, prima o poi, qualche contraddizione interna. Ma anziché trovare contraddizioni, furono invece elaborati dei modelli nei quali l’assioma della parallela veniva a cadere, dimostrando così implicitamente l’indipendenza di tale assioma dagli altri e quindi la possibilità di costruire più geometrie. Nel 1854 B. Riemann discusse all’università di Göttingen la sua tesi per la libera docenza, Sulle ipotesi che stanno alla base della geometria, in cui espone un modello di geometria non euclidea piuttosto semplice (→ Riemann, modello di), in cui, dalla negazione del quinto postulato e del secondo (sull’infinità della retta), conseguiva per esempio la proposizione che per un punto esterno non si poteva tracciare alcuna parallela a una retta data e che la somma degli angoli interni di un triangolo era maggiore di due angoli retti (geometria ellittica).

La geometria euclidea perdeva così definitivamente la sua esclusiva centralità per assumere il ruolo di caso particolare in una visione assiomatica di tipo più generale. Il quadro della geometria è stato riformulato da F. Klein nelle seguenti teorie formali:

• geometria parabolica o geometria euclidea, che comprende nel suo sistema di assiomi il quinto postulato secondo cui, dati una retta r e un punto P non appartenente a essa, si afferma l’esistenza e l’unicità di una retta passante per P e parallela a r. In tale geometria, le superfici hanno curvatura costante nulla;

• geometria iperbolica o geometria di Lobačevskij, che nega l’unicità della parallela; in essa le superfici hanno curvatura costante negativa. Un modello per questa geometria è il modello di → Beltrami;

• geometria ellittica o geometria di Riemann, che nega l’esistenza della parallela costruendo superfici in cui tutte le rette si intersecano; in essa le superfici hanno curvatura costante positiva. Oltre al modello di Riemann, un altro modello per questa geometria fu elaborato da Klein (→ Klein, modello di);

• geometria assoluta, che nel suo sistema di assiomi non comprende né il quinto postulato né la sua negazione.

La elaborazione di modelli delle geometrie non euclidee nell’ordinario spazio a tre dimensioni ha avuto grande importanza dal punto di vista logico perché dimostra l’assenza di contraddizioni nei postulati e la piena validità della costruzione geometrica fatta per via ipotetico-deduttiva.

Lo sviluppo delle geometrie non euclidee ebbe grandi ripercussioni non soltanto in campo scientifico, ma anche filosofico. Anzitutto venne meno la convinzione che i fondamenti delle teorie matematiche fossero intuitivamente evidenti e perciò universalmente veri. Il metodo assiomatico venne considerato nulla più che un procedimento assai fruttuoso per lo sviluppo delle varie branche della matematica, sicché D. Hilbert, nei Fondamenti della geometria (1899), trattò la geometria come un sistema ipotetico-deduttivo nel quale si fa astrazione dal significato intuitivo dei termini adoperati: è compito degli assiomi prescelti determinare le interpretazioni ammissibili. Si rendeva così possibile la costruzione di sistemi geometrici alternativi, donde il problema di quale sistema costituisse la corretta descrizione dello spazio fisico oggettivo.