geometria finita
geometria finita
geometria finita geometria il cui spazio ambiente è costituito da un numero finito di punti. La geometria euclidea, per esempio, non è finita, poiché una retta del piano euclideo, in virtù del secondo postulato (indefinita prolungabilità) contiene infiniti punti. Una geometria finita può avere un qualsiasi numero (finito) di dimensioni; il relativo spazio è detto spazio finito di dimensione n. Nel caso bidimensionale si hanno solo due tipi di piani finiti: affine e proiettivo. Nel piano affine è definito il parallelismo tra rette, mentre nel piano proiettivo ogni coppia di rette ha un punto di intersezione. Sia la geometria del piano affine finito sia quella del piano proiettivo finito possono essere definite assiomaticamente come segue.
Una geometria piana affine è un insieme non vuoto X, i cui elementi sono detti punti, associato a una collezione R non vuota di sottoinsiemi di X, chiamati rette, tali che:
• per ogni coppia di punti distinti esiste una e una sola retta che li contiene;
• data una retta r e un punto P, non appartenente a r, esiste una e una sola retta r′ contenente P e non avente alcun punto in comune con r (assioma della parallela);
• esiste un insieme di quattro punti a tre a tre non appartenenti a una stessa retta.
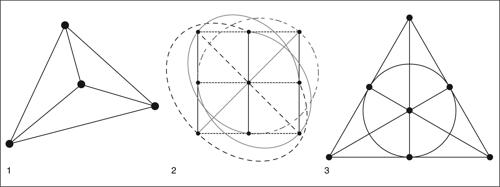
Il terzo assioma garantisce che l’insieme X non è vuoto. Il piano affine più semplice contiene esattamente quattro punti e viene detto piano affine di ordine 2. Poiché non ci sono terne di punti appartenenti a una medesima retta (punti allineati), ogni coppia di punti distinti determina un’unica retta. Ciò vuol dire che, essendo sei le coppie formate a partire da quattro punti, questo piano contiene sei rette. Un modello del piano affine di ordine 2 è rappresentato da un tetraedro: i quattro vertici sono i punti del piano, i sei spigoli le sue rette, suddivise in tre coppie di rette parallele (coppie di spigoli privi di punti comuni). In generale, un piano affine finito di ordine n possiede n2 punti e n2 + n rette; ogni retta contiene n punti, ogni punto appartiene a n + 1 rette. Così, il piano affine finito di ordine 3 contiene 12 rette, raggruppabili in quattro terne di rette parallele.
Una geometria piana proiettiva è un insieme non vuoto X, i cui elementi sono detti punti, associato a una collezione R non vuota di sottoinsiemi di X, chiamati rette, tali che:
• per ogni coppia di punti distinti esiste una e una sola retta che li contiene;
• l’intersezione di due rette distinte contiene esattamente un punto;
• esiste un insieme di quattro punti a tre a tre non appartenenti a una stessa retta.
Il terzo assioma garantisce che l’insieme X non è vuoto.
Il piano di Fano, dal nome del matematico italiano Gino Fano (1871-1952), è il più piccolo piano proiettivo (non banale) costruibile. È composto da sette punti e da sette rette. Ogni retta contiene esattamente tre punti e ogni punto appartiene esattamente a tre rette (dualità).