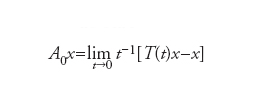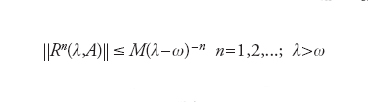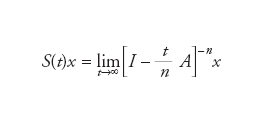generatore di un semigruppo

generatore di un semigruppo

Siano X uno spazio di Banach con norma ∣∣∙∣∣ e B(X) l’insieme degli operatori continui su di esso. Si dice semigruppo di operatori {T(t)∣t≥0} una famiglia di operatori T(t)∈B(X) che soddisfi la proprietà di semiguppo T(t)T(s)=T(t+s). Un semigruppo sarà per es. continuo, misurabile o di distribuzioni se la funzione T(t)x:ℝ→X (x∈X) è continua, misurabile o è una distribuzione (a valori in X). Consideriamo ora l’operatore

formula,

definito sull’insieme D(A₀) di tutti gli x∈X per il quale il limite esiste (detto dominio di A₀). L’operatore A₀ è detto generatore infinitesimale, la sua chiusura A generatore del semigruppo T(t). Il generatore (infinitesimale) è dunque definito come derivata rispetto al tempo di una funzione del tempo stesso, rendendo evidente l’intima connessione con la risoluzione di problemi di evoluzione. La relazione tra generatori e relativi semigruppi è completamente chiarita nel caso di operatori lineari dal teorema di Hille-Yosida. Più precisamente, T(t) ha un generatore A=A₀ (in questo caso un operatore lineare) definito su un dominio denso in X il cui risolvente R(λ,A)=(A−I)⁻¹ soddisfa le disuguaglianze

[2] formula(

ω=lim_t→∞ t⁻¹ln∣∣T(t)∣∣ è detto tipo del semigruppo T(t)) e viceversa un operatore lineare B chiuso e densamente definito che soddisfa la [1] è generatore di un semigruppo lineare continuo S(t) tale che ∣∣S(t)∣∣≤Me^ωt dato dalla formula

[3] formula.

Notiamo che quest’ultima ha senso anche nel caso A non sia lineare. La disuguaglianza [2] è soddisfatta se vale la condizione di Hille-Yosida: ∣∣R(λ,A)∣∣≤M(λ−ω)⁻¹. Il teorema di Hille-Yosida può essere generalizzato da un lato al caso di spazi vettoriali topologici e dall’altro a quello di operatori non lineari.

→ Equazioni funzionali