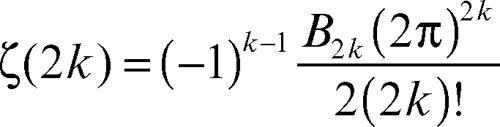Riemann, funzione zeta di
Riemann, funzione zeta di
Riemann, funzione zeta di funzione ζ(s) della variabile complessa s, definita per Re(s) > 1 (ossia nell’insieme A dei numeri complessi s con parte reale maggiore di 1) dalla serie
La serie converge in A e definisce una funzione olomorfa. La funzione ζ si estende per prolungamento analitico a tutto C, ossia all’intero piano complesso, a esclusione del punto s = 1, dove ha un polo semplice con residuo 1. Sempre per Re(s) > 1, risulta
La funzione ζ(s) si annulla nei punti s = −2n, con n intero (zeri “banali”); ha inoltre infiniti zeri nella striscia 0 < Re(s) < 1. Secondo l’ipotesi di Riemann tali zeri si trovano tutti sulla retta Re(s) = 1/2.
I valori per s = 2k, con k intero positivo, sono stati calcolati da Eulero. Risulta in generale:
dove B2k sono i numeri di → Bernoulli. Per esempio, poiché
si ha: ζ(2) = π2/6, ζ(4) = π4/90, ζ(6) = π6/945. Non è invece nota alcuna formula esplicita per i valori di ζ(2k + 1); in particolare è stato dimostrato solo nel 1979 dal matematico R. Apéry che ζ(3) (detta per questo costante di Apéry) è irrazionale.