funzione razionale

funzione razionale

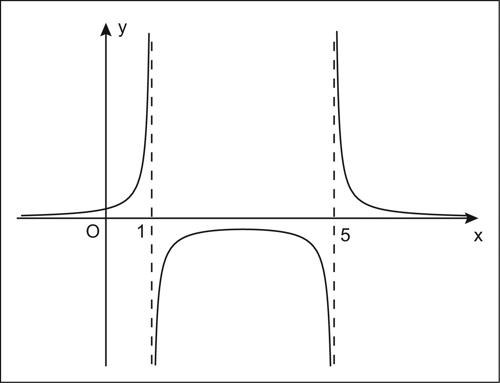
funzione razionale funzione reale che opera sulla variabile indipendente x solo tramite somma, sottrazione, moltiplicazione e loro composizioni (nel caso di funzioni razionali intere) e divisione (nel caso di funzioni razionali fratte o frazionarie). La variabile indipendente, quindi, non compare mai sotto il segno di radice. Le funzioni razionali intere sono definite per ogni x ∈ R e coincidono con le → funzioni polinomiali. Le funzioni razionali fratte sono invece definite per ogni x ∈ R tale che x non renda nullo un denominatore. Generalmente, quindi, una funzione razionale fratta risulta non definita in un numero finito di punti; spesso in corrispondenza di tali punti il grafico della funzione ha un asintoto verticale. Questo è, per esempio il caso del grafico della funzione razionale fratta

definita per x ∈ R{1, 5}, cioè per ogni reale diverso da 1 e 5. In termini generali, quindi, una funzione razionale è il quoziente di due polinomi uno dei quali può ridursi a una costante. Una particolare funzione razionale fratta ottenuta come quoziente di due polinomi di primo grado

è detta funzione omografica. Il suo grafico è dato da un’iperbole equilatera con gli asintoti paralleli agli assi cartesiani e centro nel punto (−d /c, a /c); esso può essere riportato con una opportuna traslazione a quello di un’iperbole equilatera di equazione y = k /x con k reale opportuno.