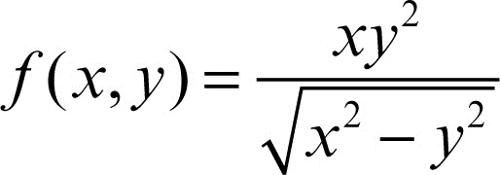funzione omogenea

funzione omogenea

funzione omogenea in termini generali, funzione ƒ definita in uno spazio vettoriale E su un corpo K espressa dall’uguaglianza ƒ(λx) = λ ⋅ ƒ(x), per ogni λ ∈ K e per ogni x ∈ E. Nel caso reale una funzione ƒ(x): Rⁿ → R, si dice (positivamente) omogenea di grado α se esiste un numero α (reale non necessariamente intero) tale che ∀λ ∈ R⁺ risulta ƒ(λx) = λ^αƒ(x). La funzione ƒ è definita in un insieme A ⊆ Rⁿ unione di semirette uscenti dall’origine (formalmente: tale che, se x ∈ A e λ ∈ R⁺, anche λx ∈ A).

Per esempio, la funzione

è omogenea di grado 2, definita in A = {(x, y) : |y| < |x|}. Se ƒ è differenziabile, un teorema di Eulero asserisce che condizione necessaria e sufficiente affinché ƒ sia omogenea di grado α è che risulti