funzione logaritmica
funzione logaritmica
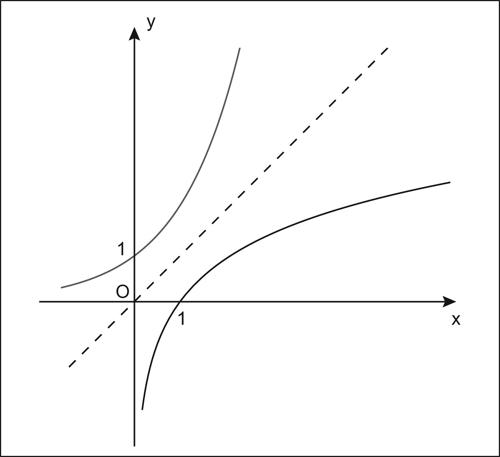
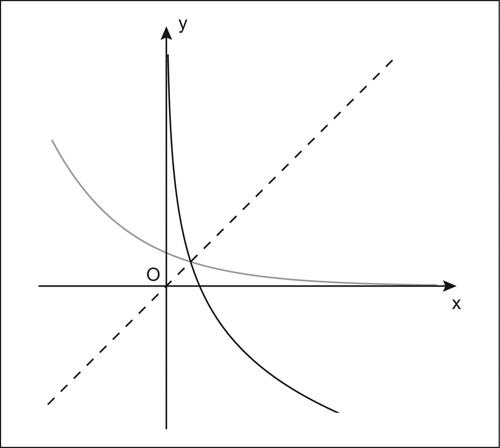
funzione logaritmica funzione inversa della → funzione esponenziale di base a; è indicata genericamente con logax, e associa a ogni numero positivo x il suo logaritmo in base a. Nel campo reale, l’esponenziale di base a > 1 è strettamente crescente, quindi anche la funzione logax è strettamente crescente (il suo grafico è il simmetrico, rispetto alla bisettrice del primo e terzo quadrante, del grafico di expax). Se invece 0 < a < 1, entrambe le funzioni ax e logax sono strettamente decrescenti (il grafico è ugualmente simmetrico di quello di expa, rispetto alla bisettrice del primo e terzo quadrante). ln ogni caso, la funzione è definita in (0, +∞).
Il grafico della funzione logaritmica ha in genere curvatura poco accentuata e per x sufficientemente grande, il tratto di curva compreso tra i punti di ascissa x e x + 1 si può quasi considerare come approssimabile da un segmento rettilineo. Questo comporta che se x + h è un numero compreso tra x e x + 1 (quindi, 0 < h < 1) il suo logaritmo può essere calcolato con buona approssimazione per → interpolazione lineare tra i rispettivi logaritmi di x e di x + 1.
Poiché vale la relazione logax = logbx / logab, la funzione logaritmica può essere studiata scegliendo la base più opportuna che, per l’analisi matematica, è il numero e di Nepero. Il logaritmo in base e viene detto logaritmo naturale o neperiano, e designato sovente con lnx, anche se spesso in analisi la scrittura logx viene intesa implicitamente come equivalente a lnx (in alcuni testi invece logx o Logx indica il logaritmo decimale di x, cioè il logaritmo in base 10 di x).
Nel campo complesso, la funzione logaritmica è una funzione polidroma: infatti, data la periodicità della funzione esponenziale in C, l’equazione ew = z ammette infinite soluzioni, per ogni z ≠ 0; tali soluzioni sono date da w = ln|z| + iarg(z), dove arg(z) rappresenta tutti i possibili argomenti di z, che differiscono tra loro per un multiplo di 2π. Pertanto gli infiniti logaritmi di un numero complesso z ≠ 0 si dispongono su una parallela all’asse immaginario, individuata da Re(w) = ln|z|, e differiscono di 2kπi, k ∈ Z. Per esempio, log(1 + i) = ln (√(2)) + i ⋅ (π/4 + 2kπ).