funzione goniometrica

funzione goniometrica

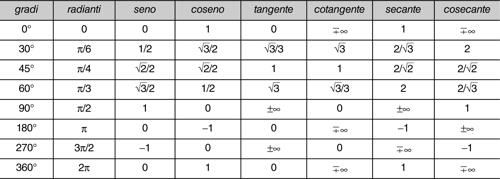
funzione goniometrica locuzione che indica una classe di funzioni reali di variabile reale, dette anche funzioni circolari o funzioni trigonometriche, il cui argomento può essere interpretato come l’ampiezza di un angolo. Esse mettono in relazione misure angolari e misure lineari e, costruttivamente, possono essere definite attraverso particolari configurazioni sulla circonferenza goniometrica. Esse sono il coseno (cos), il seno (sin o sen), la tangente (tan o tg), la cotangente (cot o cotg), la secante (sec) e la cosecante (csc o cosec).

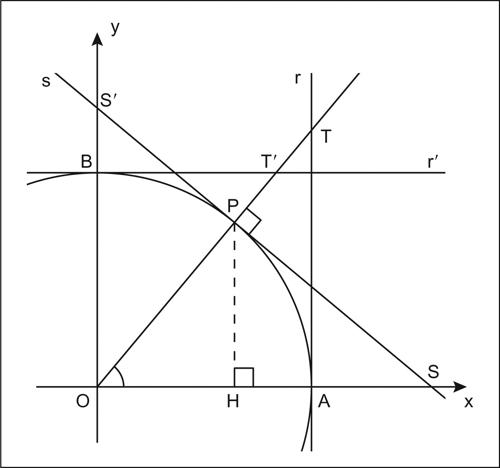
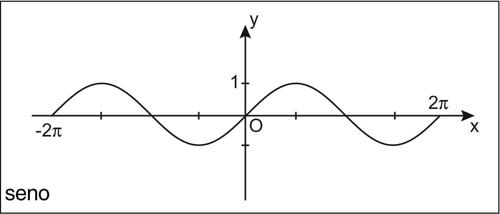
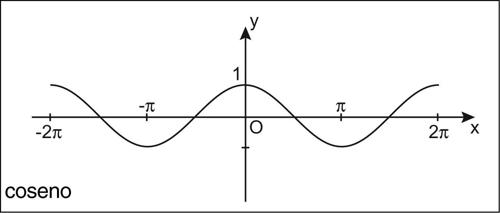
Tali funzioni possono essere tutte definite a partire dall’ampiezza di un angolo. Si consideri una circonferenza goniometrica, vale a dire una circonferenza nel piano cartesiano di centro l’origine e raggio unitario. Si fissi il punto A = (1, 0), intersezione della circonferenza con l’asse delle ascisse (detto origine degli archi) e si fissi come verso positivo delle rotazioni quello antiorario. Dato un numero reale x, si tracci a partire dall’origine degli archi un arco di lunghezza x sulla circonferenza, in senso antiorario se x è positivo, orario se invece x è negativo. Indicando con P l’estremo dell’arco tracciato, il numero x rappresenta la misura in radianti dell’angolo α sotteso all’arco tracciato, vale a dire l’area del settore circolare delimitato dai segmenti O̅A̅ e O̅P̅. Si definiscono dunque le funzioni seno e coseno della variabile x (indicate rispettivamente con i simboli sin(x) e cos(x)) rispettivamente come l’ordinata P̅H̅ e l’ascissa O̅H̅ del punto P. Segue dalla definizione che le funzioni seno e coseno sono entrambe periodiche di periodo 2π (questa è infatti la misura espressa in radianti dell’angolo giro) e che esse sono limitate, comprese tra −1 e 1; inoltre mentre il coseno soddisfa l’identità cos(x) = cos(−x), il seno soddisfa l’identità sin(x) = −sin(−x): dunque il coseno è una funzione pari, mentre il seno è una funzione dispari. Il seno e il coseno di un valore x sono legati dalla identità fondamentale della trigonometria, che riformula il teorema di Pitagora nel contesto goniometrico: sin²(x) + cos²(x) = 1.

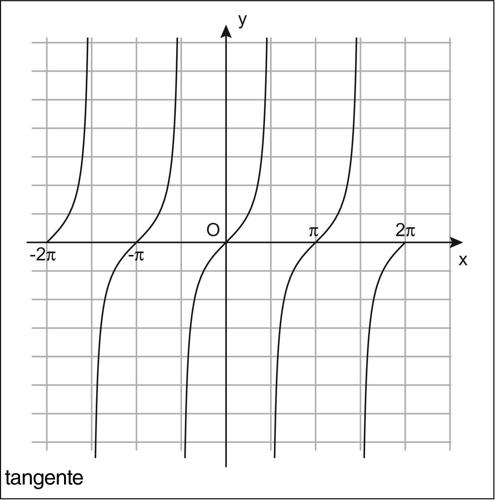
Sia r la retta tangente la circonferenza goniometrica nel punto A = (1, 0) e sia T la sua intersezione con il prolungamento del raggio della circonferenza passante per P. Si definisce allora la funzione tangente (indicata con il simbolo tan(x) o tg(x)), che associa a x l’ordinata A̅T̅ del punto T. La funzione tangente è dispari ed è periodica di periodo π. Essa è definita per ogni valore di x, eccettuati quelli per cui l’angolo sotteso all’arco AP è retto o misura 270°, vale a dire se x = (2k + 1)π/2, per ogni intero k. Ha comunque senso considerare i limiti per x che tende a tali valori: se x vi tende da sinistra (ovvero per valori minori di esso), allora il limite vale +∞, se invece x vi tende da destra (ovvero per valori maggiori di esso), allora il limite vale −∞. In corrispondenza di questi valori della variabile x, la funzione tangente ha pertanto un asintoto verticale.

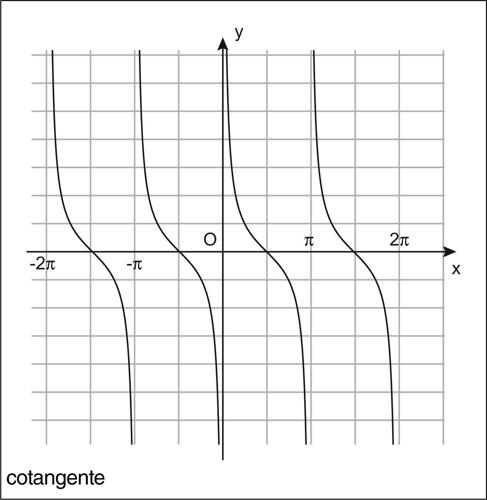
Similmente a quanto fatto per la tangente, sia r′ la retta tangente la circonferenza goniometrica nel punto B = (0, 1) e sia T′ la sua intersezione con il prolungamento del raggio della circonferenza passante per P. Si definisce allora la funzione cotangente (indicata con il simbolo cot(x) o ctg(x)), che associa a x l’ascissa B̅T̅̄′ del punto T′. Similmente al caso della tangente, la cotangente è una funzione dispari ed è periodica di periodo π. Essa è definita per ogni valore di x, eccettuati quelli per cui l’angolo sotteso all’arco AP è l’angolo piatto o l’angolo giro, vale a dire se x = kπ, per ogni intero k. Tuttavia ha senso considerare i limiti per x che tende a tali valori: se x vi tende da sinistra (ovvero per valori minori di esso), allora il limite vale −∞, se invece x vi tende da destra (ovvero per valori maggiori di esso), allora il limite vale +∞. In corrispondenza di questi valori della variabile x, la cotangente ha pertanto un asintoto verticale.

La tangente e la cotangente di un angolo sono esprimibili a partire dalle funzioni seno e coseno come segue:

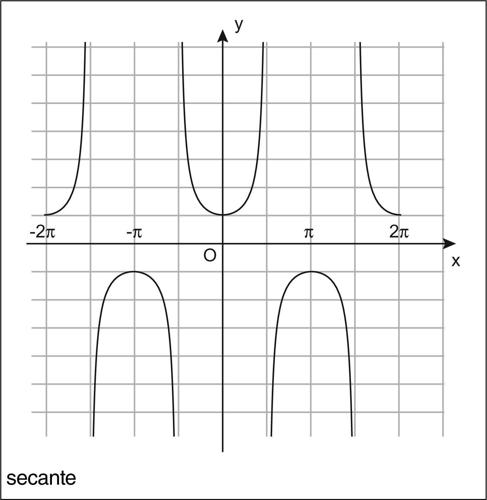
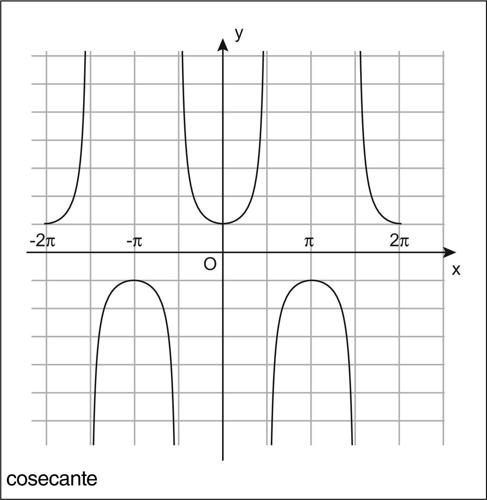
Sia s la retta tangente la circonferenza goniometrica in P e siano S e S′ le sue intersezioni rispettivamente con l’asse delle ascisse e con l’asse delle ordinate. Si definiscono allora le funzioni secante e cosecante (indicate rispettivamente con i simboli sec(x) e csc(x)), che associano a x rispettivamente l’ascissa O̅S̅ del punto S e l’ordinata O̅S̅′ del punto S′. La secante e la cosecante sono entrambe funzioni periodiche di periodo 2π; mentre la secante è una funzione pari, la cosecante è una funzione dispari. La secante è definita per ogni valore della variabile x, eccettuati quelli per cui l’angolo sotteso all’arco AP è l’angolo retto o l’angolo di 270°, vale a dire se x = (2k + 1)π/2, per ogni intero k. Considerando i limiti per x che tende a questi valori, nel primo caso si trova che, se x tende da sinistra a π/2 (o a un valore della forma x = (4k + 1)π/2), allora il limite vale +∞, se invece x vi tende da destra, allora il limite vale −∞. Nel secondo caso, se x tende da sinistra a 3π/2 (o a un valore della forma x = (4k + 3)π/2), allora il limite vale −∞, se invece x vi tende da destra, allora il limite vale +∞. In corrispondenza di questi valori della variabile x, la secante ha pertanto un asintoto verticale. Similmente alla secante, la cosecante è definita per ogni valore della variabile x, eccettuati quelli per cui l’angolo sotteso all’arco AP è l’angolo piatto o l’angolo giro, vale a dire se x = kπ, per un opportuno intero k. Considerando i limiti per x che tende a questi valori, allora nel primo caso si trova che, se x tende da sinistra a π (o a un valore della forma x = (2k + 1)π), allora il limite vale +∞, se invece x vi tende da destra, allora il limite vale −∞. Nel secondo caso, se x tende da sinistra a 2π (o a un valore della forma x = 2kπ), allora il limite vale −∞, se invece x vi tende da destra, allora il limite vale +∞. In corrispondenza di questi valori della variabile x, la secante ha pertanto un asintoto verticale.

La secante e la cosecante di un angolo sono rispettivamente i reciproci del coseno e del seno dello stesso angolo, cioè:

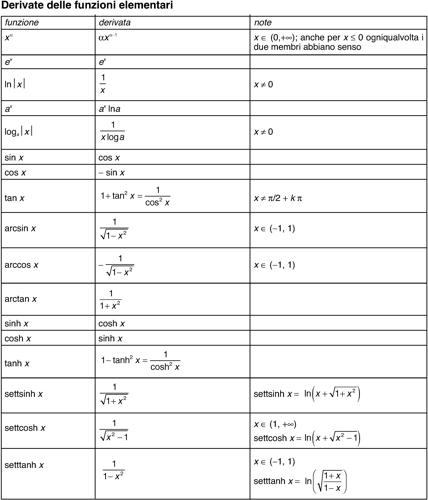
Oltre alla identità fondamentale della trigonometria, che riformula il teorema di Pitagora nel contesto goniometrico (sin²(x) + cos²(x) = 1), vi sono numerose altre formule trigonometriche, cioè relazioni che legano tra loro le funzioni goniometriche: per ognuna di esse vi sono formule di addizione e sottrazione, di duplicazione e di bisezione, e inoltre le formule di → Briggs, le → formule parametriche, le formule di prostaferesi, le formule di → Werner. Le curve piane ottenute come grafici di funzioni goniometriche sono dette curve trigonometriche piane: in particolare, si hanno la sinusoide (ottenuta come grafico del seno), la cosinusoide (ottenuta come grafico del coseno), la tangentoide (ottenuta come grafico della tangente), la cotangentoide (ottenuta come grafico della cotangente), la secantoide (ottenuta come grafico della secante), la cosecantoide (ottenuta come grafico della cosecante). Le funzioni goniometriche sono tutte funzioni periodiche, continue e differenziabili infinite volte nel loro insieme di definizione (si veda la tavola delle derivate delle funzioni elementari). Esse sono tutte sviluppabili in serie di potenze e coincidono con tale sviluppo (→ funzione analitica; per lo sviluppo in serie di seno e coseno si vedano le voci → seno e → coseno).