funzione goniometrica inversa

Enciclopedia della Matematica (2017)

funzione goniometrica inversa


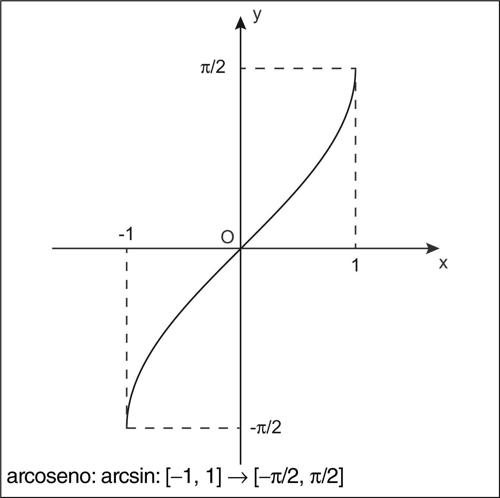
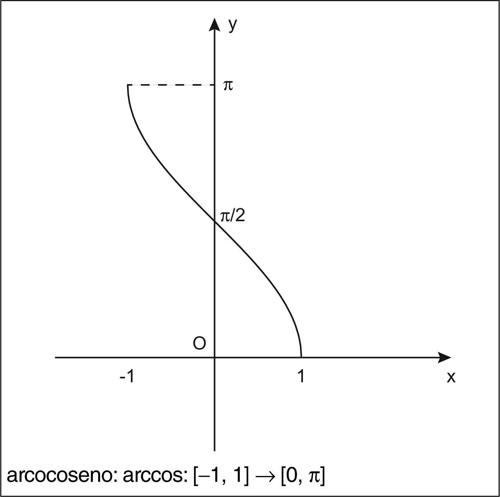
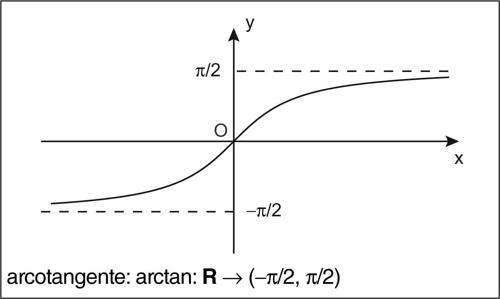
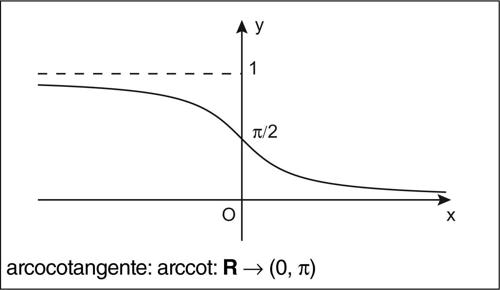
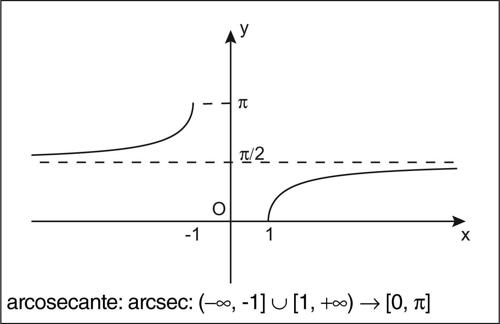
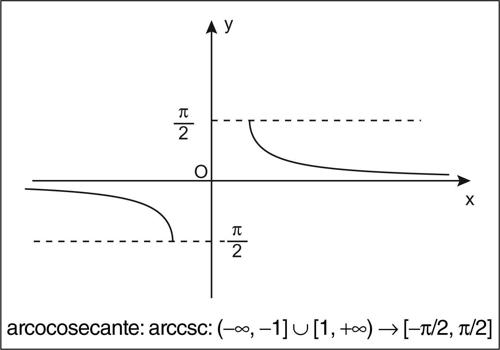
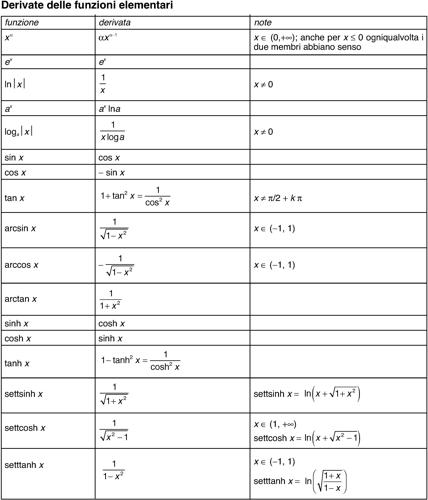
funzione goniometrica inversa ognuna delle funzioni inverse associate alle corrispondenti funzioni goniometriche. Le funzioni goniometriche sono tutte funzioni periodiche e quindi, non essendo biunivoche, non sono globalmente invertibili. Se però il dominio viene opportunamente ristretto esse diventano funzioni biunivoche e quindi invertibili. Convenzionalmente, al fine di ottenere delle funzioni monotòne, gli intervalli a cui esse sono ristrette per essere invertite sono o l’intervallo [0, π] (nel caso del coseno, della cotangente e della secante), oppure l’intervallo [−π/2, π/2] (nel caso del seno, della tangente e della cosecante). Il dominio della funzione inversa sarà pertanto dato dall’immagine di tale intervallo tramite la funzione che si desidera invertire. In questo senso, pertanto, a ogni funzione goniometrica è possibile associare una funzione inversa. Si ottengono in questo modo le funzioni goniometriche inverse: l’→ arcoseno (indicato con il simbolo arcsin o sin−1 e definito sull’intervallo [−1, 1]), l’→ arcocoseno (indicato con il simbolo arccos o cos−1 e definito sull’intervallo [−1, 1]), l’ → arcotangente (indicata con il simbolo arctan o tan−1 e definita su tutto R), l’→ arcocotangente (indicata con il simbolo arccot e cot−1 e definita su tutto R), l’arcosecante (indicata con il simbolo arcsec o sec−1 e definita per |x| ≥ 1), l’→ arcocosecante (indicata con il simbolo arccsc o csc−1 e definita per |x| ≥ 1). Le funzioni goniometriche inverse sono tutte continue e differenziabili infinite volte nel loro dominio (si veda la tavola delle derivate delle funzioni elementari).

Enciclopedia della Matematica fig lettf 04120 001.jpg
Enciclopedia della Matematica fig lettf 04120 002.jpg
Enciclopedia della Matematica fig lettf 04120 003.jpg
Enciclopedia della Matematica fig lettf 04120 004.jpg
Enciclopedia della Matematica fig lettf 04120 005.jpg
Enciclopedia della Matematica fig lettf 04120 006.jpg
Enciclopedia della Matematica tab lettf 04120 001.jpg

Vedi anche
arcocotangente In trigonometria, si dice a. di x l’arco la cui cotangente trigonometrica è x; simbolo: arccotangx (o arccotgx). La funzione y=arccotangx è quindi funzione inversa della funzione circolare ‘cotangente’. secante fig. Asecante In geometria, retta s. (o semplicemente s.) una curva piana c in un punto P è ogni retta r che passi per P e non sia tangente in P a c (fig. A); può però accadere che una retta r s. in P sia tangente alla curva c in un altro punto Q (fig. B); si chiama piano s. il piano che interseca una ... arcoseno In trigonometria, si dice a. di x l’arco il cui seno è x; simbolo: arcsen x. A un dato valore del seno non corrisponde un solo arco, ma infiniti (per es., gli archi il cui seno è 1 sono espressi, in gradi, dalla formula: 90°±k 360°, con k intero). Cioè, mentre la funzione x=seny è a un solo valore, la ... arcocoseno In trigonometria, si dice a. di x l’arco il cui coseno è x; simbolo: arccos x. La funzione y=arccosx è quindi funzione inversa della funzione circolare ‘coseno’. È una funzione a moltivalori, analoga in ciò all’arcoseno.
Tag
Vocabolario
goniomètrico
goniometrico goniomètrico agg. (pl. m. -ci). – Che si riferisce alla goniometria o al goniometro: misurazioni goniometriche.
goniometrìa
goniometria goniometrìa s. f. [comp. di gonio- e -metria]. – 1. In topografia, misurazione degli angoli zenitali e azimutali fatta col goniometro. 2. In matematica, genericam., teoria della misurazione degli angoli.