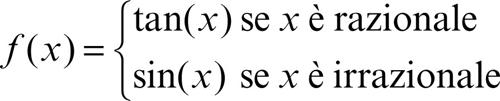funzione essenzialmente limitata

funzione essenzialmente limitata

funzione essenzialmente limitata è così detta una funzione ƒ: Ω ⊆ R → R se esiste una costante M > 0 tale che la disuguaglianza |ƒ(x)| ≤ M sia verificata per quasi ogni argomento x di Ω, cioè per tutti gli x ∈ Ω, eccettuato al più un insieme di misura nulla. Per esempio, la funzione

pur non essendo limitata è essenzialmente limitata in R, essendo |ƒ(x)| ≤ 1 tranne per x appartenente all’insieme dei numeri razionali che ha misura di Lebesgue nulla.