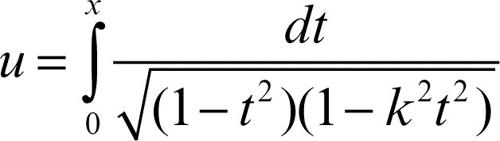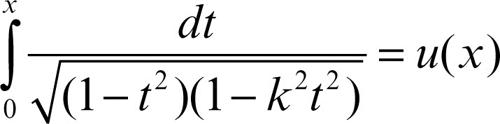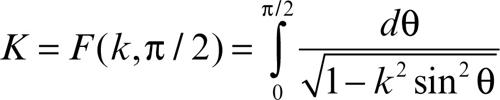funzione ellittica

funzione ellittica

funzione ellittica funzione u(x) definita a partire dall’integrale ellittico cosiddetto di prima specie

considerato quale funzione del suo estremo superiore d’integrazione:

con x ∈ [−1, 1]. Se il modulo k vale 0, questa funzione è elementare e vale u = arcsin(x). È perciò invertibile e si ottiene x = sin(u). Se k = 1 analogamente l’integrale è elementare, dunque è significativo solo il caso 0 < k < 1. Poiché u(x) è strettamente crescente, è invertibile e si può ottenere x in funzione di u: tale funzione (pure strettamente crescente) si indica con x = sn(u) (si legge «esse enne di u») e viene detta seno amplitudine. Essa è in realtà funzione anche del modulo k. Il valore x = 1 viene raggiunto in corrispondenza dell’integrale ellittico completo

Come la funzione seno, anche sn(u) è dispari, e si ha sn(−K) = −1, sn(0) = 0, sn(K) = 1. Si introducono poi le funzioni

e

entrambe pari e simili alla funzione coseno, essendo cn(0) = dn(0) = 1, cn(K) = 1,

(k′ si dice modulo complementare). Queste tre funzioni sono le funzioni ellittiche secondo Jacobi. Nei casi limite si ha:

• per k = 0, sn(u) = sin(u), cn(u) = cos(u), dn(u) = 1, K = π/2;

• per k = 1 invece è sn(u) = tanh(u), cn(u) = dn(u) = sech(u), K = ∞.

L’analogia prosegue con:

• le identità: sn²(u) + cn²(u) = 1, dn²(u) + k ²sn²(u) = 1;

• le derivate: sn′(u) = cn′(u)dn(u), cn′(u) = −sn(u)dn(u), dn′(u) = −k ²sn(u)cn(u);

• le formule di addizione e altre (si veda la tavola delle funzioni speciali).

Le formule di addizione permettono di estendere il dominio delle funzioni ellittiche a tutto R e si ha che sn(u) e cn(u) sono periodiche di periodo 4K, mentre dn(u) ha periodo 2K. Infine, è possibile estendere le funzioni ellittiche al campo complesso, ottenendo delle funzioni meromorfe, aventi un doppio periodo: oltre ai periodi reali, infatti, le funzioni seno, coseno e delta amplitudine hanno rispettivamente i periodi complessi 2iK′, 2K + 2iK′, 4iK′, essendo K′ = F(k′, π/2). Entro ciascun parallelogramma di periodicità, i cui lati sono individuati dai due periodi, ciascuna delle funzioni ellittiche ammette due zeri semplici e due poli semplici.

Nella teoria generale delle funzioni analitiche, si chiamano funzioni ellittiche le funzioni doppiamente periodiche in C, i cui periodi 2ω₁ e 2ω₂ hanno rapporto complesso: esse si riducono alle funzioni ellittiche secondo Jacobi se in ogni parallelogramma di periodicità ci sono due poli semplici, mentre se vi è un polo doppio si ottengono le funzioni ellittiche secondo Weierstrass. Ogni altra funzione ellittica è esprimibile mediante funzioni di questi due tipi.

Tra le applicazioni delle funzioni ellittiche secondo Jacobi, oltre alla determinazione della lunghezza di un arco di ellisse, si ha la soluzione dell’equazione differenziale del pendolo semplice. Se ψ(t) rappresenta l’angolo formato dal pendolo con la verticale, si ha l’equazione ψ″ + ω²sinψ = 0, con ω² = g /l, che nel caso delle piccole oscillazioni si linearizza in ψ″ + ω²ψ = 0, ma in generale, poste le condizioni ψ = 0 per t = 0, ψ′ = 0 per ψ = α < π/2 (α è quindi la massima elongazione del pendolo) ha la soluzione ψ = 2arcsin(k sn(ωt)), k = sinα/2. Il periodo delle oscillazioni risulta T = 4K /ω, ed è quindi funzione crescente di α. Mediante funzioni ellittiche è possibile ottenere delle formule esplicite per le soluzioni delle equazioni algebriche di quinto e sesto grado (secondo i lavori di C. Hermite e F. Brioschi).