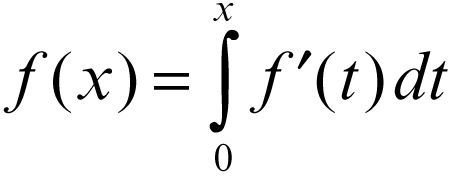Vitali, funzione di
Vitali, funzione di
Vitali, funzione di esempio di funzione uniformemente ma non assolutamente continua. Per costruirla, si segua il procedimento che conduce alla cosiddetta polvere di → Cantor. Nel terzo centrale (1/3, 2/3) dell’intervallo [0, 1] si ponga ƒ(x) = 1/2. Nei due intervalli (1/9, 2/9) e (7/9, 8/9) corrispondenti alla seconda iterazione si ponga rispettivamente ƒ(x) = 1/4 e ƒ(x) = 3/4. Nei quattro intervalli successivamente ottenuti si ponga ƒ(x) = (2k − 1)/8, e così via: in generale dunque la funzione assume valori costanti della forma (2k − 1)/2n negli intervalli aperti del complementare A dell’insieme di Cantor. Su tale insieme ƒ(x) risulta crescente, anche se su ciascun intervallo è costante, e ha quindi derivata nulla. Il codominio di ƒ(x) è, fino al livello di definizione considerato, numerabile, anche se A ha misura unitaria. La funzione limite si ottiene come prolungamento per continuità all’insieme C di Cantor. La funzione ottenuta può essere definita analiticamente nel modo qui di seguito descritto. Posto ƒ(1) = 1, si esprima ogni x < 1 in base 3: se x ∈ A, almeno una cifra della sua rappresentazione è uguale a 1 (la prima cifra per il primo intervallo; la seconda per quelli del secondo passaggio e così via). Negli estremi sono possibili due rappresentazioni, se si accettano anche quelle con periodo 2: per esempio
Dunque l’insieme C si caratterizza per il fatto che ogni x ∈ C ammette (almeno) una rappresentazione ternaria che non contiene la cifra 1. Il valore ƒ(x) è allora ottenuto sostituendo in tale rappresentazione alla cifra 2 la cifra 1, e interpretando il risultato in base 2. Per esempio,
Come si vede, i due valori coincidono tra loro e con quello assunto in tutto l’intervallo (1/3, 2/3). La funzione risulta continua e crescente e il suo codominio è tutto [0, 1]: ciò mostra che C ha la cardinalità del continuo, essendo l’immagine di A numerabile. La sua derivata esiste in A, e quindi quasi ovunque in [0, 1], e vale 0; tuttavia non si ha
perché tale integrale, che esiste nel senso di Lebesgue, è identicamente nullo.