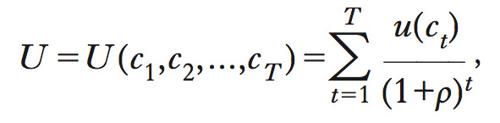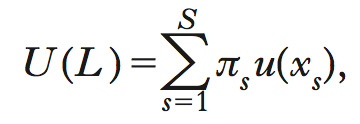utilità, funzione di
utilità, funzione di
Contesti decisionali e modellizzazioni
Se si indica con xn, (n=1,2,...N), la quantità della merce n e con x=(x1,x2,...,xN) un paniere di merci, la funzione di utilità U=U(x) offre una rappresentazione analitica delle preferenze; in altri termini, essa esprime in forma numerica il grado di soddisfazione che il consumatore attribuisce al possesso o al consumo del paniere x. Ne deriva la possibilità di stabilire una scala del gradimento per un paniere piuttosto che per un altro attraverso il confronto – in termini di maggiore, uguale o minore – dell’utilità assegnata agli stessi. La teoria economica di impostazione neoclassica individua, nella massimizzazione dell’utilità soggetta a vincoli di fattibilità e di bilancio, il criterio della razionalità di comportamento degli agenti. Di seguito si illustrano alcuni tipici contesti decisionali, in cui il consumatore potrebbe venire a trovarsi, associando al paniere di beni le possibili forme della funzione di utilità.
Scelte di consumo in contesto statico
Si adotti la convenzione di trasformare ogni merce che arreca una pena nel suo opposto, per es., l’inquinamento atmosferico in aria pulita, e si consideri quindi il paniere x costituito unicamente di beni in senso stretto, disponibili in un dato momento di tempo. Una prima ipotesi è che l’utilità dipenda separatamente dalle quantità consumate dei singoli beni e sia quindi del tipo separabile in senso additivo: U=u1(x1)+u2(x2)+...+uN(xN), con la supposizione che l’utilità marginale sia positiva e decrescente. Una forma particolare di funzione separabile in senso additivo è quella quasi lineare U=u1(x1)+m, in cui si considera che il paniere sia costituito da una merce specifica, per es., x1, e da una merce composita, espressa in termini di quantità di moneta m destinata all’acquisto di tutti gli altri beni. Una seconda e più generale ipotesi è che la funzione di utilità assuma la forma non separabile: U=U(x1,x2...,xN); ciò significa che l’utilità marginale del consumo di ciascun prodotto dipende dall’intero insieme di beni a disposizione del consumatore. Ai fini della determinazione delle funzioni individuali di domanda, l’ipotesi di decrescenza del saggio marginale di sostituzione (➔ saggio; sostituibilità) nel consumo prende ora il posto dell’ipotesi di decrescenza dell’utilità marginale. ● Nelle precedenti formulazioni si è assunto che l’utilità di un agente dipenda unicamente dai propri consumi. Ripetuti risultati empirici, che rivelano comportamenti ispirati a sentimenti di altruismo e di equità (➔ economia comportamentale), mettono in discussione la validità di tale ipotesi. Per tener conto di questi risultati, è necessario supporre che la funzione di utilità dipenda anche dai consumi di altri agenti, in grado di esercitare un’esternalità, positiva o negativa, sul benessere del singolo.
Scelte intertemporali di consumo e di risparmio
Secondo la teoria del ciclo vitale di F. Modigliani, il risparmio ha il ruolo fondamentale di consentire il livellamento dei consumi, da cui dipende il benessere del consumatore, in presenza di un andamento dei redditi disuguale nell’arco di vita di una persona. Nello studio delle scelte intertemporali è abituale l’uso di una funzione di utilità separabile in senso additivo che ha come argomenti il consumo aggregato dei diversi periodi di vita, e precisamente
dove ρ indica il tasso di preferenza intertemporale. Anche in questo caso, gli studi empirici rivelano deviazioni sistematiche dal comportamento ottimale desumibile da tale funzione di utilità; e mettono in luce, in particolare, la presenza di fenomeni di incoerenza temporale delle scelte.
Decisioni sotto incertezza
La considerazione dell’incertezza modifica profondamente il contesto decisionale degli agenti, poiché implica che le conseguenze di una scelta possano essere diverse − più o meno favorevoli − a seconda del verificarsi di condizioni da loro non controllabili. Sotto l’ipotesi che l’incertezza sia codificabile attraverso l’individuazione di un insieme S di stati di natura, mutuamente escludibili, e che sia possibile assegnare una probabilità oggettiva πs, (s=1,2...,M) al verificarsi di ciascuno di essi, J. Von Neumann e O. Morgenstern (The theory of games and economic behavior, 1944) hanno enunciato il principio dell’utilità attesa, secondo cui l’utilità di un prospetto incerto o lotteria L con esiti monetari xs è
dove u(xs) è la funzione di utilità della quantità di moneta xs. L.J. Savage (The foundations of statistics, 1954), utilizzando precedenti fondamentali risultati di B. De Finetti (La prevision: ses lois logiques, ses sources subjectives, «Annales de l’Institute Henri Poincaré», 1937, 7,1), ha esteso la teoria dell’utilità attesa a situazioni di incertezza probabilistica. Supponendo che l’insieme degli stati di natura sia infinito anziché finito e la funzione di densità di probabilità degli stati di natura sia normale, l’utilità attesa viene a dipendere unicamente dalla media μ e dalla varianza σ2 della funzione di densità: U(L)=V(μσ2). Questa particolare forma della funzione di utilità attesa trova ampia applicazione negli studi di finanza. I risultati empirici mettono seriamente in dubbio l’attendibilità della teoria dell’utilità attesa come strumento descrittivo dei comportamenti in condizioni di incertezza. La ricerca è stata particolarmente attiva in questo campo e ha portato a numerose e profonde riformulazioni della teoria (➔ anche neuroeconomia; prospect theory).