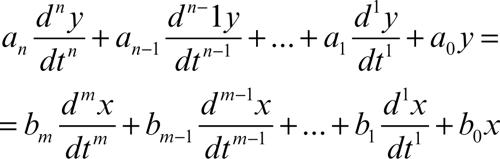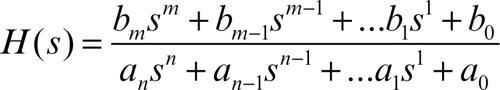trasferimento, funzione di
trasferimento, funzione di
trasferimento, funzione di rappresentazione matematica della relazione tra l’uscita e l’ingresso di un sistema fisico il cui comportamento può essere descritto da un sistema differenziale lineare invariante. Dette y(t) l’uscita del sistema e x(t) il suo ingresso e assumendo che il comportamento del sistema possa essere descritto mediante una relazione del tipo
si definisce funzione di trasferimento, indicata con H(s), il rapporto tra la trasformata di Laplace (→ Laplace, trasformazione di) della risposta forzata yƒ (t) a un segnale di ingresso causale x(t) e la trasformata di Laplace dell’ingresso stesso:
Nell’ipotesi che siano nulle le condizioni iniziali, risulta:
La funzione di trasferimento è una caratteristica intrinseca del sistema differenziale che rappresenta ed è indipendente dalla natura del segnale di ingresso x(t). Il grado del denominatore della funzione di trasferimento è sempre maggiore o uguale a quello del numeratore; infatti, affinché il sistema sia fisicamente realizzabile, deve valere n ≥ m. La funzione di trasferimento può essere interpretata come la trasformata di Laplace della risposta forzata a un impulso. Inoltre essa consente di calcolare la risposta forzata a un qualunque segnale causale di cui sia possibile calcolare la trasformata di Laplace. La funzione di trasferimento consente inoltre di dedurre le condizioni di stabilità del sistema, studiando gli zeri del denominatore, cioè i suoi poli: il sistema è stabile se e solo se nessun polo ha parte reale positiva e i poli con parte reale nulla sono semplici; il sistema è asintoticamente stabile se e solo se i poli hanno tutti parte reale negativa.