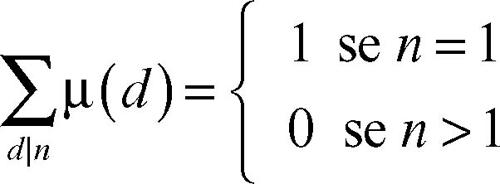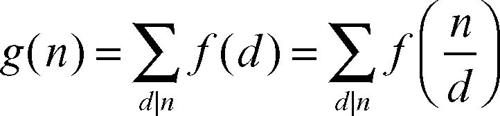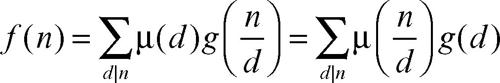Mobius, funzione di
Mobius, funzione di
Möbius, funzione di funzione aritmetica µ(n) che a un numero naturale n associa il valore (−1)k se n ha k fattori primi tutti distinti e associa il valore 0 se n ha fattori primi ripetuti. Per esempio, µ(5) = µ(30) = −1, µ(6) = 1, µ(12) = 0. Poiché 1 non deve essere considerato primo, si pone µ(1) = 1, in quanto 1 ha zero fattori primi. Risulta
dove la scrittura «d|n» che compare nella sommatoria indica che «d divide n». Questa funzione si incontra in diverse questioni di teoria dei numeri. La trasformata di Möbius di una funzione ƒ(n) è la funzione
l’inversione di tale trasformazione si ottiene dalla formula
Per esempio, n è la trasformata di Möbius della funzione toziente di → Eulero φ(n), e quindi
