funzione cubica
funzione cubica
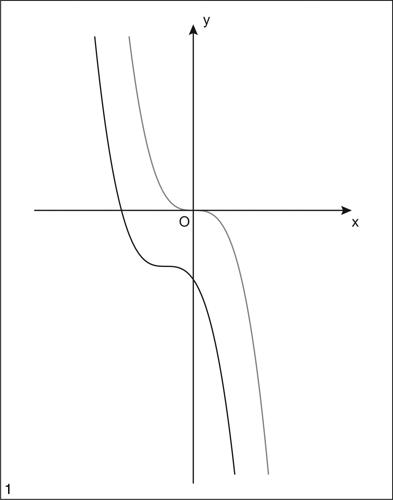
funzione cubica funzione reale di una variabile reale espressa da un polinomio di terzo grado. Una funzione cubica ƒ(x) è definita per ogni x ∈ R, è continua e derivabile. Se è del tipo y = ax 3 la funzione è crescente o decrescente a seconda del segno del coefficiente a e il suo grafico ha un punto di flesso orizzontale, ascendente in un caso, discendente nell’altro. Lo stesso andamento si mantiene se il grafico della funzione subisce una traslazione (di vettore v(u, v)) e, quindi, l’espressione della funzione è riconducibile alla forma y − v = a(x − u)3. Per esempio, il grafico della funzione
ha lo stesso andamento della funzione
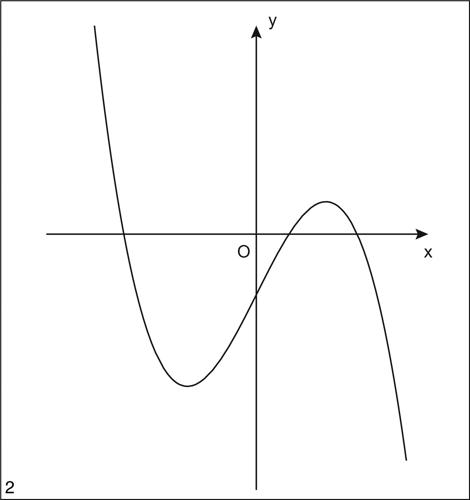
a cui corrisponde nella traslazione di vettore v(−1, −2). Nel caso più generale, invece, la funzione pur avendo un andamento “complessivamente” crescente o decrescente, ha un flesso non orizzontale e il suo grafico è caratterizzato da un punto di massimo relativo e un punto di minimo relativo; resta il fatto che il suo andamento complessivo è determinato dal segno del coefficiente del termine di terzo grado. Per esempio la funzione
si può dire “complessivamente” decrescente nel senso che il suo limite per x tendente a −∞ è +∞ e il suo limite per x tendente a +∞ è −∞.