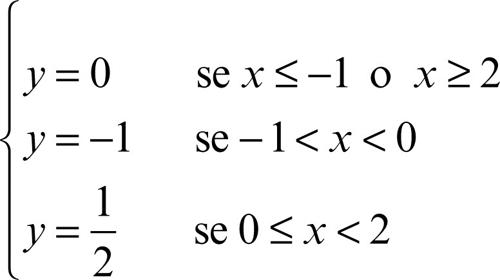funzione costante
funzione costante
funzione costante funzione ƒ che, qualunque siano i valori delle sue variabili indipendenti, assume lo stesso valore. Nel caso di funzione reale di una variabile: X → Y essa associa a ogni valore x ∈ X lo stesso valore y ∈ Y e il suo grafico è conseguentemente una retta parallela all’asse delle ascisse. Per esempio, il grafico della funzione reale y = k con k ∈ R è la retta parallela all’asse delle ascisse che interseca in (0, k) l’asse delle ordinate. Una funzione polinomiale è costante se e solo se è espressa da un polinomio di grado 0.
La composizione di una qualsiasi funzione g con la funzione costante è una funzione costante. Se ƒ è una funzione di due variabili x e y, la sua espressione è del tipo ƒ(x, y) = k e il suo grafico è un piano parallelo al piano coordinato xy e a quota k da esso.
Una funzione di una variabile è costante in un intervallo [a, b] se in tale intervallo è derivabile e la sua derivata è uniformemente nulla per ciascun punto dell’intervallo. Se è possibile ripartire un intervallo [a, b] in n sottointervalli aventi intersezione vuota e tali che la loro unione dia l’intervallo stesso, è possibile definire per casi una funzione (→ funzione definita per casi) che sia costante in ciascuno dei sottointervalli anche se i valori rispettivamente assunti in essi non sono uguali. Per esempio è possibile definire per casi in R la seguente funzione in una incognita:
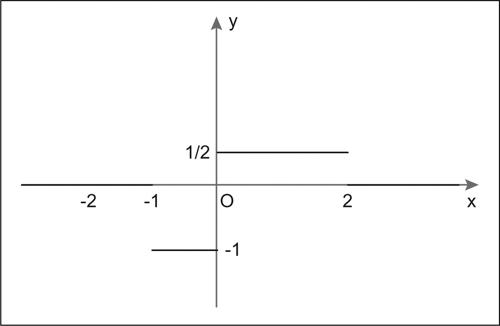
È una funzione definita per ogni x ∈ R, costante in ciascun sottointervallo anche se assume valori diversi in essi. Il suo grafico è composto da un insieme di tratti paralleli all’asse delle ascisse.
Una funzione di questo tipo è detta funzione costante a tratti o funzione a gradini. Un esempio di funzione costante a tratti è la funzione theta di → Heaviside (detta anche funzione gradino) che per x < 0 vale 0 e per x > 0 vale 1. Una funzione continua a tratti è anche detta step function.
