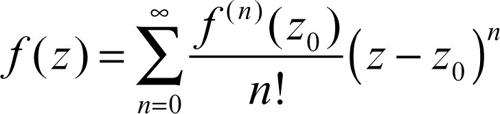funzione analitica

funzione analitica

funzione analitica in analisi, funzione complessa di variabile complessa, ƒ(z), che in un aperto Ω ⊆ C ammette derivata complessa

Una funzione analitica in Ω è anche detta funzione olomorfa in Ω. Se ƒ è differenziabile, condizione necessaria e sufficiente affinché sia analitica è la cosiddetta condizione di → Cauchy-Riemann. La derivata è data allora da

Una funzione analitica è nota quando sia data su una linea chiusa σ, essendo calcolabile mediante le formule integrali di → Cauchy; da queste si deduce che ƒ è dotata di derivata di ogni ordine e che è sviluppabile in serie di → Taylor

in un intorno di ogni suo punto di analiticità. Viceversa, ogni serie di potenze in C avente raggio di convergenza R > 0 ha come somma una funzione olomorfa nel cerchio di convergenza; essa può essere prolungata al di fuori di questo cerchio mediante sviluppi in serie, detti elementi analitici, aventi centro in altri punti del cerchio iniziale, e così procedendo per successive estensioni finché possibile (prolungamento analitico con il metodo di Weierstrass). In questo modo è però possibile che, ritornando all’elemento di partenza, il valore della funzione risulti differente da quello iniziale: si dice allora che la funzione è multiforme o che è una funzione polidroma.

I punti in cui ƒ non è continua si chiamano punti di singolarità di ƒ; le singolarità isolate si distinguono in poli e singolarità essenziali. Se z₀ è un polo, risulta

e lo sviluppo in serie di → Laurent contiene un numero finito di termini. Una funzione ammette solo singolarità polari se e solo se è una funzione razionale; una funzione che al finito ammette solo singolarità polari si dice meromorfa.

In una singolarità essenziale, invece,

non esiste; vale invece il teorema di → Picard, che afferma che in un intorno qualsiasi di z₀ la funzione ƒ assume tutti i valori complessi, eccettuato al più uno. Per esempio, la funzione e^z ammette una singolarità essenziale all’infinito, e l’equazione e^z = λ ammette infinite soluzioni, per λ ≠ 0, date da

Il più debole teorema di → Casorati-Weierstrass afferma invece che l’immagine di tale intorno è densa nella sfera complessa.

Il primo principio di identità delle funzioni analitiche afferma che due funzioni analitiche ƒ e g sono identiche se coincidono in uno stesso punto z₀, insieme con tutte le loro derivate: ƒ ⁽ⁿ⁾(z₀) = g⁽ⁿ⁾(z₀). Il secondo principio afferma che ƒ e g sono identiche se coincidono in infiniti punti dell’insieme di analiticità Ω, aventi un punto di accumulazione z₀ ∈ Ω; in particolare, se coincidono lungo un arco di linea qualsiasi. Di conseguenza, una proprietà espressa da un’identità analitica, se vera nel campo reale, continua a valere anche in C, salvo naturalmente nelle singolarità delle funzioni considerate (principio di permanenza delle proprietà analitiche). Per esempio, l’identità cos²x + sin²x = 1 rimane vera in tutto C: cos²z + sin²z = 1, ma non se ne può dedurre che |cos z| ≤ 1, in quanto la funzione |z| non è analitica.