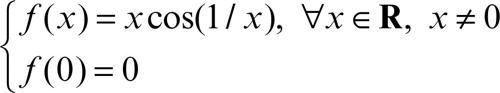funzione a variazione limitata
funzione a variazione limitata
funzione a variazione limitata in analisi, funzione ƒ(x), definita in un intervallo [a, b], che è tale in [a, b] se l’estremo superiore delle somme
al variare della sequenza a = x0 < x1 < ... < xn = b è finito. Tale estremo superiore viene detto variazione totale di ƒ(x) in [a, b] ed è indicato con Vab(f ).
Una funzione a variazione limitata è limitata ma non necessariamente continua; tuttavia può possedere al più un’infinità numerabile di discontinuità di prima specie (di salto). Viceversa, esistono funzioni continue che non sono a variazione limitata: per esempio, la funzione continua definita da
non è a variazione limitata in [0, 1]. Si dimostra che una funzione è a variazione limitata se e solo se è la differenza di due funzioni monotòne (nello stesso verso). Ogni funzione a variazione limitata possiede quasi ovunque una derivata, che risulta integrabile secondo Lebesgue. La sua derivata nel senso delle distribuzioni è una misura limitata. Lo spazio delle funzioni a variazione limitata si indica in genere con BV([a, b]) (dall’inglese bounded variation). ed è uno spazio di Banach con la norma Vab(f ).
La nozione si può generalizzare a più variabili.