Sheffer, funtori di

Sheffer, funtori di

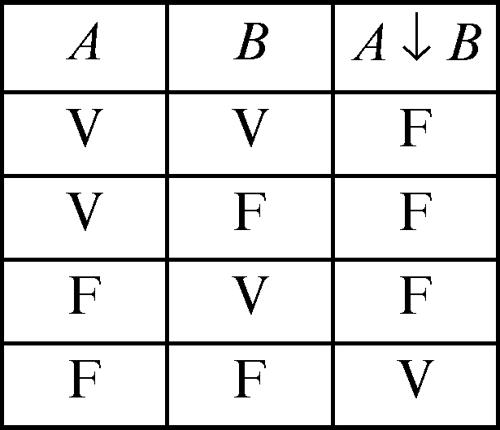
Sheffer, funtori di espressione che denota due connettivi logici, il primo indicato con il simbolo ↓, il secondo indicato con il simbolo |. Il primo operatore è utilizzato per comporre due enunciati A e B in modo da formare l’enunciato A ↓ B corrispondente nel linguaggio naturale all’espressione «né A né B». La sua tavola di verità è:

Si può verificare che l’enunciato A ↓ B è logicamente equivalente (→ equivalenza logica) all’enunciato ¬(A ∨ B) scritto con i connettivi usuali, e quindi a ¬A ∧ ¬B (per questo è anche detto negazione congiunta o, data la sua forma, funzione freccia di Sheffer).

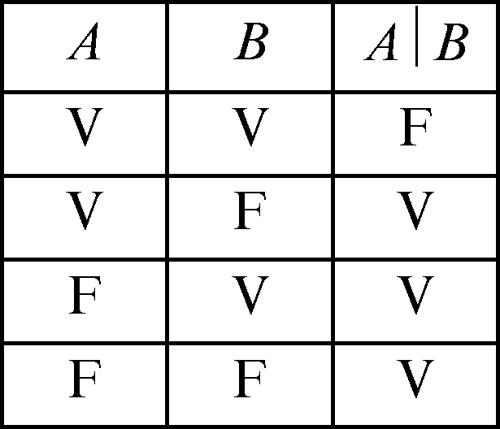
Il secondo funtore di Sheffer si applica a due enunciati A e B per formare l’enunciato A | B il cui significato è «A è incompatibile con B». La sua tavola di verità è:

L’enunciato A|B è logicamente equivalente a ¬(A ∧ B) e, quindi, a ¬A ∨ ¬B (per questo è anche detto negazione alternativa o barra di Sheffer). Utilizzando i due funtori di Sheffer è possibile ricostruire tutti gli altri connettivi; ciò significa che, dato un enunciato α scritto usando i connettivi usuali, è possibile scrivere un enunciato α′ logicamente equivalente ad α in cui compaiono solo i funtori di Sheffer: per questo si dice che i funtori di Sheffer formano una base di connettivi. I funtori di Sheffer sono gli unici due connettivi binari che formano una base: per mezzo di essi è possibile ricostruire il connettivo unario ¬ dato che ¬A è logicamente equivalente sia ad A ↓ A sia ad A |A.