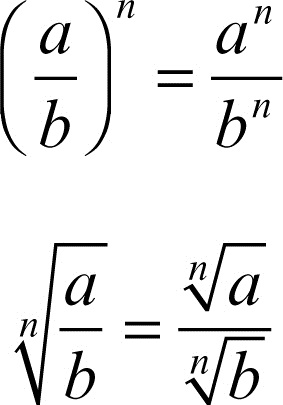frazione

frazione

frazione → rapporto tra due numeri interi, di cui il secondo diverso da 0. Per indicare il rapporto m : n = mn⁻¹ si scrive

(o anche m/n), che si legge «m ennesimi» oppure «m fratto n»: m è detto il numeratore (perché indica il numero di parti che si considerano) e n è detto il denominatore della frazione (perché denomina, cioè definisce, le parti uguali in cui si divide l’unità). Per esempio, i 3/4 («tre quarti») dell’unità si ottengono dividendo l’unità in quattro parti uguali e considerando tre di tali parti; una frazione è nulla (e quindi equivale a zero) quando il numeratore è uguale a 0. Due frazioni m/n e m′/n′ si dicono equivalenti se mn′ = m′n; due frazioni sono equivalenti se sono ottenibili l’una dall’altra moltiplicando o dividendo numeratore e denominatore per uno stesso numero intero diverso da zero. L’insieme delle classi di frazioni equivalenti costituisce l’insieme Q dei numeri razionali: ogni numero razionale può essere espresso come prodotto di un numero intero m per l’inverso di un altro numero intero n non nullo, ossia nella forma mn⁻¹.

Una frazione si dice ridotta ai minimi termini (o irriducibile) se il numeratore e il denominatore sono numeri interi primi fra loro, vale a dire se non ammettono divisori comuni. Per ridurre una frazione ai minimi termini occorre dividere numeratore e denominatore per il loro massimo comune divisore (mcd): questa operazione viene detta semplificazione della frazione; più in generale si parla di semplificazione di una frazione ogniqualvolta si dividono numeratore e denominatore per uno stesso fattore comune. Una frazione si dice apparente se il numeratore è un multiplo intero del denominatore: ciò equivale a dire che la frazione ridotta ai minimi termini ha denominatore 1 e può essere identificata con un numero intero. Per esempio, la frazione apparente 6/3 equivale al numero intero 2.

Per addizionare (rispettivamente sottrarre) due frazioni che abbiano lo stesso denominatore, si addizionano (rispettivamente, si sottraggono) i numeratori lasciando invariato il denominatore: per esempio, 1/3 + 4/3 = 5/3. Similmente, per confrontare due frazioni aventi lo stesso denominatore, si confrontano i numeratori: per esempio 9/15 è maggiore di 5/15, perché 9 è maggiore di 5. Per addizionare, sottrarre e confrontare due frazioni con diversi denominatori, ci si riconduce al caso di frazioni con lo stesso denominatore attraverso la riduzione a denominatore comune, vale a dire si determinano due forme equivalenti delle due frazioni date aventi lo stesso denominatore. L’addizione, la sottrazione o il confronto tra le due frazioni date potranno in questo modo essere effettuate sulle due forme equivalenti, che avranno lo stesso denominatore. Una possibile riduzione a denominatore comune è ottenibile moltiplicando il numeratore e il denominatore di ciascuna frazione per il denominatore dell’altra: ciò equivale a scegliere come denominatore comune il prodotto dei denominatori delle due frazioni date. Si ottiene così la seguente definizione formale della somma di due frazioni arbitrarie

e similmente per la differenza. Una migliore scelta per il denominatore comune è il minimo comune multiplo (mcm) dei denominatori delle due frazioni: questa scelta, in generale, ha l’effetto di diminuire il numero di fattori comuni tra il numeratore e il denominatore del risultato ottenuto. Per esempio, volendo sommare 1/30 e 3/50, si considera il minimo comune multiplo dei loro denominatori, che è 150, e le due frazioni, espresse in centocinquantesimi, sono 5/150 e 9/150: si ottiene dunque 1/30 + 3/50 = 5/150 + 9/150 = 14/150 = 7/75.

Il prodotto di due frazioni si ottiene moltiplicando rispettivamente i numeratori e i denominatori fra loro:

In generale, se due frazioni sono ridotte ai minimi termini, non è detto che anche il loro prodotto lo sia: per semplificarlo, è possibile operare direttamente sui fattori del prodotto, prima di operare la moltiplicazione, eliminando eventuali fattori comuni tra i numeratori e i denominatori. Per esempio, nella moltiplicazione 2/3 ⋅ 3/5 è possibile semplificare il denominatore del primo fattore con il numeratore del secondo fattore: si ottiene dunque 2/3 ⋅ 3/5 = 2 ⋅ 1/5 = 2/5. Ogni frazione diversa da zero (il cui numeratore sia cioè diverso da zero) è invertibile, esiste cioè una frazione, detta la sua inversa (indicata con l’esponente ⁻¹), che moltiplicata per essa dà come risultato 1. L’inversa di una frazione si ottiene scambiando tra loro il numeratore e il denominatore:

L’inversa di 2/3 è per esempio 3/2, mentre l’inversa di 3 è 1/3. Per dividere due frazioni, si moltiplica la prima per l’inversa della seconda:

Per esempio, 2/3 : 3/5 = 2/3 ⋅ 5/3 = 10/9. La potenza di una frazione si ottiene elevando a potenza sia il numeratore sia il denominatore; analogamente la radice di una frazione si ottiene estraendo le radici sia del numeratore sia del denominatore:

Seguendo la regola dei segni per il prodotto, una frazione è positiva se numeratore e denominatore hanno lo stesso segno; è negativa se hanno segni discordi.

Una frazione si dice decimale se il suo denominatore è una potenza di 10, si dice invece diadica se il suo denominatore è una potenza di 2. Non tutte le frazioni sono scrivibili in forma decimale: ciò equivale infatti a darne una scrittura come numero decimale finito, vale a dire con un numero finito di cifre decimali. Le uniche frazioni esprimibili in forma decimale sono quelle per cui il denominatore della relativa forma ridotta ai minimi termini non ha fattori diversi da 2 e 5: tutte le altre frazioni daranno luogo a numeri decimali periodici, con infinite cifre decimali.

Le frazioni si classificano in frazioni proprie, quando il numeratore è minore del denominatore, e frazioni improprie, quando il numeratore è maggiore del denominatore oppure è a esso uguale (e allora equivale a 1): una frazione impropria si riduce dunque alla somma di una frazione apparente (vale a dire un numero intero) e di una frazione propria. Per esempio, 3/5 è una frazione propria, mentre invece 14/3 è impropria e si riduce alla somma 12/3 + 2/3 = 4 + 2/3. Nei paesi anglosassoni, per queste frazioni, si utilizza anche la scrittura come numero misto, per cui, per esempio, 14/3 si scrive come 4²/₃. Si dice frazione complementare di una frazione propria quella che sommata a essa dà risultato 1: per esempio, la frazione complementare di 2/3 è 1/3.