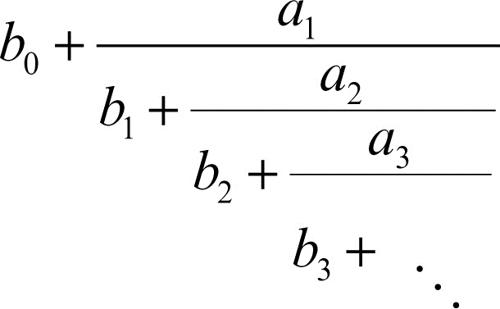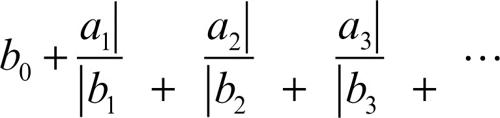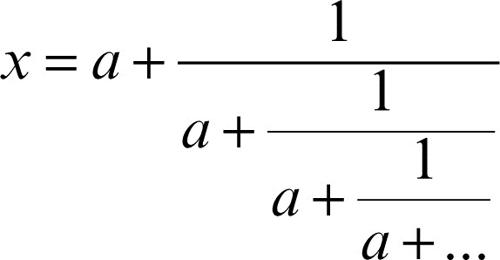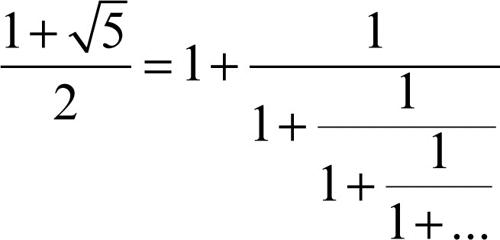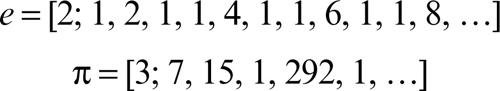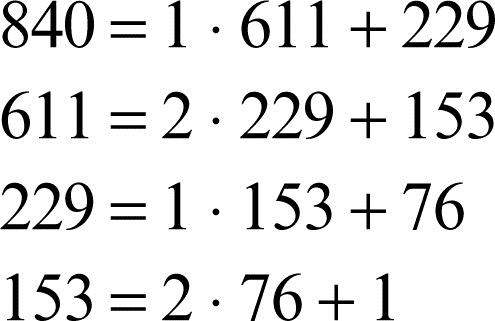frazione continua

frazione continua

frazione continua in aritmetica, espressione della forma

usualmente scritta, per motivi tipografici, in linea (ma si noti la posizione dei segni +) come

o, ancor più semplicemente, come

In forma simbolica, come per le serie e i prodotti infiniti, si scrive anche

la lettera K essendo l’iniziale della parola tedesca Kettenbruch (traducibile come frazione incatenata). I primi sviluppi di un numero reale in frazione continua sono dovuti al matematico e astronomo italiano P.A. Cataldi, che nel 1613 dà,

e al matematico irlandese W. Brouncker, che nel 1659 fornisce

cioè una formula contenente una frazione continua, per il calcolo approssimato di π. Esempi di frazioni continue sono quelle che definiscono il numero di Nepero e o quella che individua la radice positiva di una equazione di secondo grado della forma x ² = ax + 1:

che per a = 1 dà il numero aureo Φ:

Nella scrittura

i numeri, reali o complessi, a_n e b_n, con a_n ≠ 0, sono detti rispettivamente numeratore e denominatore parziale n-simo e, genericamente, elementi della frazione continua.

La approssimante o ridotta n-sima di una frazione continua è una frazione continua finita espressa dal numero

ottenuto troncando lo sviluppo al denominatore b_n. La frazione continua si dice convergente a z se

II valore di ƒ_n come rapporto del numeratore e denominatore n-simo A_n e B_n della frazione continua si può ottenere mediante le formule di ricorrenza A_n = b_nA_n−1 + a_nA_n−2, B_n = b_nB_n−1 + a_nB_n−2, a partire da A₋₁ = 1, A₀ = b₀, B₋₁ = 0, B₀ = 1.

Le frazioni continue

si dicono equivalenti se hanno le stesse ridotte n-sime; la condizione necessaria e sufficiente affinché ciò avvenga è che esista una successione {r_n} di costanti non nulle, con r₀ = 1, tali che

È sempre possibile assumere

Particolarmente importanti sono le frazioni continue regolari (o normali), in cui a_n = 1 e b_n ∈ N; la frazione continua si scrive allora nella forma [b₀; b₁ b₂, b₃, ...]. Ogni numero reale x positivo si può espandere in frazione continua regolare mediante le formule b_n = [x_n], dove x₀ = x, x_n = 1/mant(x_n − 1), dove [x] è la parte intera e mant(x) la mantissa di x. Come visto precedentemente, risulta per esempio

così come risultano:

(quest’ultima frazione continua non ammette una formula generale per i coefficienti).

Le frazioni continue regolari periodiche corrispondono a irrazionali quadratici. Le ridotte di ordine pari e quelle di ordine dispari formano una coppia di classi contigue che definisce x. Il numero x è razionale (x ∈ Q) se la frazione continua che lo esprime è finita; in tal caso lo sviluppo di x in frazione corrisponde all’algoritmo di Euclide. Per esempio dati i due numeri 840 e 611, in base all’algoritmo di Euclide, poiché si hanno le uguaglianze

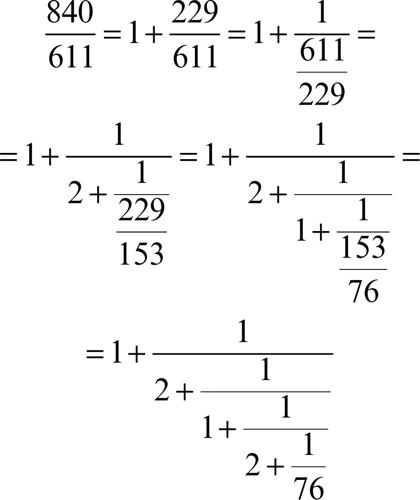
si ha che

In questo caso il numero razionale 840/611 è sviluppato in una frazione continua finita.