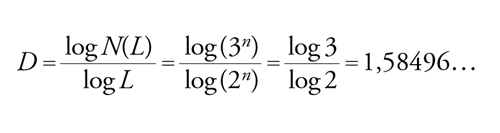Frattali
Frattali
La geometria frattale permette di caratterizzare le strutture che godono della proprietà di invarianza di scala. Il termine frattale (dal latino fractus, rotto o frammentato) è stato introdotto nel 1975 da Benoît Mandelbrot. In pochi anni questo concetto è divenuto molto popolare in diverse discipline come matematica, fisica, biologia ed economia. "La geometria frattale è uno di quei concetti che a prima vista ispira scetticismo, ma in un secondo momento diventa così naturale da domandarsi perché sia stato sviluppato solo recentemente". Queste parole di Michael V. Berry descrivono appropriatamente l'impressione che questa nuova geometria, pur non usuale rispetto ai canoni matematici, rappresenti invece un concetto naturale e inevitabile per la descrizione di un gran numero di fenomeni, sia naturali sia sociali.
Da un punto di vista strettamente matematico i concetti di dimensione non intera e di autosomiglianza sono noti da molto tempo. Fin dal 1919 essi furono discussi da Felix Hausdorff in una forma simile a quella attuale e si possono incontrare anche nei lavori di Henri Poincaré del 1885. Anche Karl Weierstrass, Niels F.H. von Koch, Pierre J.L. Fatou, Gaston M. Julia e altri autori hanno studiato oggetti matematici con queste proprietà.
Per lungo tempo però questi concetti, che descrivono strutture fortemente irregolari, sono stati relegati ai margini della matematica e quasi completamente ignorati nelle altre discipline, poiché la maggior parte dei metodi matematici e geometrici usuali sono basati sul concetto di regolarità o analiticità. Ciò significa per esempio che data una curva è possibile definire la sua tangente in modo univoco per ogni suo punto e quindi, per scale sufficientemente piccole, tale curva può essere approssimata dalla sua tangente e perde ogni altra struttura. Nelle strutture frattali o autosimili invece si ha la ripetizione della stessa struttura a tutte le scale e quindi una qualunque sottostruttura possiede ancora tutta la complessità della struttura originale.
L'autosomiglianza, o invarianza di scala, implica pertanto una grande irregolarità che non è possibile descrivere con i metodi matematici tradizionali. È facile constatare, comunque, che in natura l'irregolarità è molto comune, come dimostrano chiaramente le strutture di piante, montagne, nuvole, fulmini e così via.
Anche l'anatomia offre meravigliosi esempi di strutture frattali, come le arterie e i bronchi nei polmoni. Basti pensare che la superficie effettiva attraverso cui l'ossigeno viene assorbito nei polmoni ha un'area di circa due campi da tennis, il tutto racchiuso in un volume di estensione estremamente minore. Questa caratteristica è resa possibile dalla presenza di strutture frattali, che sono state ampiamente utilizzate attraverso la selezione evolutiva per l'ottimizzazione della fisiologia delle strutture biologiche.
Strutture frattali in natura
I casi storicamente più noti di strutture fortemente irregolari che hanno stimolato l'indagine scientifica sono il fiocco di neve e la dinamica browniana (microscopica) degli atomi in un fluido, osservata per la prima volta da Jean Perrin. Nel caso del fiocco di neve è facile osservare che il suo contorno è talmente variabile che non è possibile definire una tangente in modo univoco in ogni punto.
Lo stesso problema si ha se si cerca di definire la lunghezza di un litorale frastagliato, come per esempio la costa della Gran Bretagna. Alla scala di una carta geografica le strutture minime definibili sono dell'ordine dei chilometri. Guardando più attentamente la costa si potranno osservare anche anfrattuosità (strutture) dell'ordine di centinaia di metri, poi dei metri, dei centimetri e dei millimetri fino al livello del singolo granello di sabbia. Aumentando a mano a mano la precisione della misura, le nuove strutture che appaiono contribuiscono alla lunghezza totale del litorale. Tale lunghezza è pertanto definibile solo una volta assegnata una lunghezza minima delle strutture che si prendono in considerazione. Se si fa tendere a zero questa lunghezza minima, la lunghezza del litorale tende a divergere fino a che viene raggiunta una scala minima alla quale la proprietà di autosomiglianza si interrompe. Lo stesso avviene ovviamente al di sopra della scala dell'intera Gran Bretagna.
In generale dovremmo quindi aspettarci che nei fenomeni naturali le eventuali proprietà frattali siano definite all'interno di una scala minima e una massima. A livello matematico invece il processo si può estendere idealmente da zero all'infinito. Naturalmente l'intervallo deve essere abbastanza grande da poter definire le proprietà frattali in modo adeguato e la situazione può cambiare considerevolmente nel caso di fenomeni distinti. Si noti che lo stesso problema si presenta nell'utilizzo dei concetti geometrici usuali come il piano e la linea.
Ritornando alle traiettorie delle molecole osservate da Perrin, esse risultano tanto più irregolari a causa delle collisioni tra molecole quanto più è piccola la scala considerata. Solo a grandi scale e per tempi lunghi le traiettorie acquistano una certa regolarità e infatti lo studio del moto browniano si è tradizionalmente focalizzato sugli aspetti matematici di questo punto di vista.
L'approccio scientifico tradizionale tende alla ricerca di uniformità e armonia nelle strutture matematiche e le eventuali irregolarità vengono considerate come imperfezioni. Questo ha portato a trascurare tutta una serie di fenomeni che, seppure molto comuni e di notevole importanza, non presentano tali caratteristiche. La geometria frattale ribalta questo punto di vista e permette di trattare le irregolarità come entità intrinseche e quantificabili in modo matematico. Si deve a Mandelbrot l'aver mostrato, con numerosi esempi, che concetti considerati curiosità astratte, costituiscono invece un apparato matematico di nuovo tipo per la descrizione delle strutture intrinsecamente irregolari.
La dimensione frattale
Consideriamo come esempio elementare di struttura frattale l'intreccio (gasket) di Sierpinski, costruibile con il processo iterativo indicato nella fig. 2. Questa struttura è definita dividendo un triangolo equilatero in quattro sottotriangoli equilateri. Si lascia il triangolo centrale vuoto e si dividono gli altri tre nello stesso modo per poi procedere iterando la costruzione. A rigore, la completa invarianza di scala implicherebbe un numero infinito di iterazioni. Nella fig. 2, vediamo il risultato di sei iterazioni e i piccoli triangoli in colore (che andrebbero anch'essi divisi) rappresentano la più piccola scala che consideriamo in questa struttura. Consideriamo questa lunghezza minima come unitaria e contiamo il numero di triangoli di lato uno (in colore) contenuti in una struttura di lato L definita a partire dal vertice superiore. Il numero N(L) corrisponde a un volume generalizzato in funzione della scala L scelta.
Un modo spesso utilizzato in fisica per definire la dimensione di un oggetto è per mezzo dell'esponente che lega il volume alla lunghezza. Nei sistemi geometricamente regolari la dimensione corrisponde a un numero intero. Per esempio, nel caso di una linea abbiamo N(L)=CL dove C è una costante dipendente dall'unità di misura utilizzata, mentre per un piano abbiamo N(L)=CL2 e per un volume N(L)=CL3. La dimensione può quindi essere identificata come l'esponente che lega la massa (o volume generalizzato) alla lunghezza caratteristica del sistema.
Possiamo allora definire una dimensione frazionaria o frattale D tramite l'esponente che connette N(L) a L:
[1] N(L)=CLD.
Dalla fig. 2 possiamo osservare che, aumentando la lunghezza di un fattore 2, la massa (numero di triangolini scuri) aumenta di un fattore 3. Abbiamo quindi che a una lunghezza L=2n, corrisponde una massa pari a N(L)=3n. La dimensione frattale risulta allora
[2] formula
Concludiamo che per l'intreccio di Sierpinski volume e lunghezza sono connessi da un esponente non intero. Questa relazione corrisponde a una legge di scala in cui l'invarianza, intrinseca nella costruzione della figura, viene rappresentata matematicamente da un andamento a potenza con esponente non intero.
Questa situazione ha importanti conseguenze concettuali e pratiche, non solo sulla natura delle fluttuazioni intrinseche a ogni scala ma anche sull'assenza di una scala caratteristica, a parte quelle minima e massima, in cui si sviluppano le proprietà di autosomiglianza. Matematicamente si può pensare a un processo al limite in cui la scala minima tende a zero o la massima a infinito. In questo caso si ottiene una struttura frattale ideale con le stesse proprietà a tutte le scale.
Nelle analisi di situazioni reali si può ragionevolmente parlare di proprietà di invarianza di scala se queste sono definite su un regime abbastanza esteso da poter definire in modo chiaro e non ambiguo un comportamento a legge di potenza rispetto, per esempio, a un andamento esponenziale o gaussiano.
Da un punto di vista matematico, la dimensione frattale viene definita attraverso il più rigoroso concetto di ricoprimento. Si considera il numero di oggetti compatti di grandezza ε necessari per 'riempire' una struttura di grandezza L: per il caso euclideo l'analogia è il rivestimento di un pavimento con delle mattonelle. La dimensione frattale è quindi definita dalla relazione
[3] formula,
considerata nel limite ε→0.
Nel caso dell'intreccio di Sierpinski applicando questa procedura per la dimensione frattale si ottiene lo stesso risultato, ma per strutture più complesse i due procedimenti possono non essere coincidenti. Per esempio, la relazione fisica massa-lunghezza si riferisce al limite di grandi scale, quella definita dal ricoprimento al limite di scale infinitesime.
Questa generalizzazione del concetto di dimensione riguarda le proprietà metriche del sistema, ma non necessariamente quelle topologiche. Le prime si riferiscono essenzialmente a quanta massa è contenuta in un dato volume, le seconde sono definite dal numero di gradi di libertà necessari per identificare un punto della struttura. Se consideriamo un filo, la sua dimensione topologica è sempre uno mentre quella metrica (frattale) dipende da come è disposto nello spazio, per esempio se è esteso o compatto. In termini rigorosi si definisce frattale un sistema in cui la dimensione metrica o di Hausdorff è maggiore della sua dimensione topologica.
Proprietà delle strutture frattali
Il fatto che una struttura sia autosimile o frattale implica la sua invarianza per trasformazioni di scala: ingrandendo ogni suo dettaglio si ottiene di nuovo la struttura originale. Nei semplici esempi discussi in precedenza, questa proprietà è imposta a priori dalla costruzione geometrica. Nei processi fisici e naturali è invece la dinamica a generare le strutture e produrre spontaneamente queste proprietà. La caratterizzazione di queste strutture con strumenti matematici richiede l'uso di metodi appropriati che sono spesso diversi da quelli usuali. Se per esempio consideriamo l'intreccio di Sierpinski e cerchiamo di calcolare la densità dei punti occupati, otteniamo che, per grandi scale, questa densità tende a zero. Ciò è dovuto al fatto che la struttura è asintoticamente dominata dalle zone vuote, che prevalgono di gran lunga su quelle piene.
Consideriamo una tipica funzione di correlazione, per esempio la densità condizionale
[4] Γ(r)=〈n(r0)n(r0+r)〉0.
La funzione n(r) vale uno se il punto r appartiene alla struttura considerata, zero altrove. La funzione Γ(r) ci fornisce la probabilità condizionale che, dato un punto appartenente alla struttura, ci sia un altro punto di essa traslato di r da questo. La media si riferisce a tutte le possibili scelte del primo punto. Questa densità condizionale è proporzionale alla massa generalizzata divisa per il volume e quindi
[5] formula
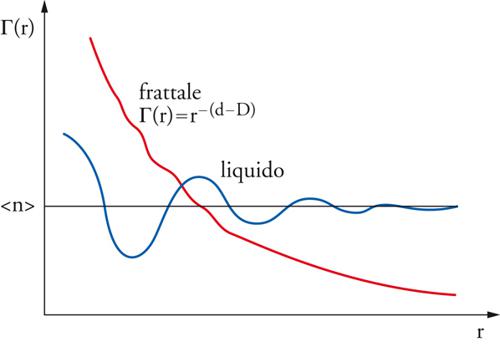
dove d è la dimensione dello spazio in cui la struttura è definita r=∣r∣. Dato che la dimensione frattale di un insieme è sempre minore di quella dello spazio in cui è definito, abbiamo il sorprendente risultato che la densità condizionale tende a zero a grandi scale e quindi non è possibile definire una densità media: una proprietà alquanto inusuale rispetto al comportamento dei sistemi tradizionali come solidi, liquidi e gas. Questo decadimento della densità condizionale è lo stesso (in media) per qualunque punto del sistema e rappresenta un'implicazione sottile e non intuitiva delle proprietà di invarianza di scala. La fig. 3 mostra la funzione di correlazione per un liquido ordinario e per una struttura frattale. Nel caso del liquido essa oscilla a piccole distanze per poi convergere a una densità media quando le distanze stesse divengono grandi, mentre nel caso del frattale la funzione decade con continuità e tende asintoticamente a zero.
Possiamo anche notare che nelle strutture geometriche artificiali l'autosimilarità è esatta per un insieme discreto di trasformazioni, mentre in genere nelle strutture reali essa è definita in senso statistico.
È bene notare che il concetto di autosomiglianza o invarianza di scala non è nuovo nella fisica. Esso è ben noto nello studio delle proprietà critiche delle transizioni di fase ed è stato di cruciale importanza nella formulazione della teoria del gruppo di rinormalizzazione. In questo caso, però, l'autosimilarità era considerata una peculiarità della competizione tra ordine e disordine alla temperatura critica per sistemi in equilibrio termodinamico. Ora possiamo invece osservare che l'invarianza di scala è una proprietà ben più generale ed è presente in molti fenomeni di non equilibrio in cui questa proprietà risulta da un processo di autoorganizzazione critica. Questa visione permette di capire anche perché le strutture con tali caratteristiche sono in realtà molto comuni e non circoscritte a situazioni peculiari come l'equilibrio critico.
Una caratteristica di questo campo di ricerca è il ruolo centrale che ha avuto il calcolatore. Per problemi di tipo tradizionale il suo uso ha permesso di ottenere soluzioni accurate di problemi complicati, ma per le strutture frattali e in genere complesse il suo ruolo è stato molto più rilevante. I modelli matematici in quest'ultimo caso sono infatti di carattere iterativo e quindi particolarmente adatti a essere studiati con simulazioni al calcolatore, un fatto che ha agevolato la scoperta che alcuni sistemi all'apparenza molto semplici possono generare strutture di grande complessità. Tali simulazioni rappresentano pertanto una sorta di esperimenti numerici per l'esplorazione e lo studio di strutture frattali e in questo senso sono molte le affinità con la teoria del caos deterministico.
La struttura frattale dell'Universo a grande scala
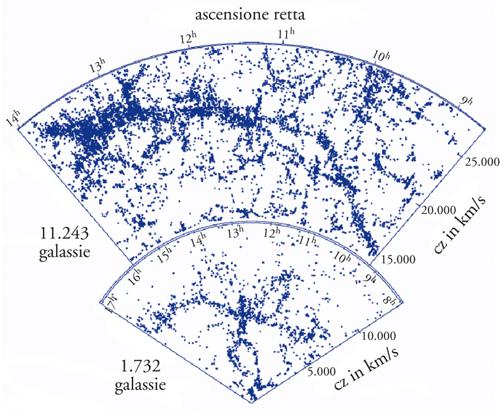
Un esempio particolarmente rilevante dell'applicazione di questi concetti è fornita dalle strutture osservate nell'Universo a grande scala. Nella fig. 4 viene riportata la distribuzione delle galassie in tre dimensioni: la parte inferiore corrisponde al progetto CfA (Center for Astrophysics) degli anni Novanta mentre quella superiore ai primi dati del nuovo progetto SDSS (Sloan digital sky survey) che sarà terminato nel 2008. La figura corrisponde alla proiezione su un piano di una porzione di volume tridimensionale. Come si può osservare, la scala delle strutture aumenta con il volume considerato e la definizione di una densità media appare problematica anche con la semplice analisi visiva.
L'analisi statistica tradizionale di questi dati è basata sull'assunzione a priori che l'Universo sia abbastanza omogeneo a scale relativamente piccole e che nelle distribuzioni osservate sia possibile definire una densità media intrinseca. In questa prospettiva, l'analisi viene fatta attraverso le funzioni di correlazione tipiche della fisica dei liquidi e dei sistemi regolari. La fig. 4 evidenzia però che la distribuzione delle galassie non è affatto regolare ma presenta grandi ammassi e regioni quasi vuote su scale dell'ordine di quelle dell'intero sistema. Si può quindi riconsiderare l'analisi statistica facendo uso di metodi più generali che tengano conto anche della possibilità di proprietà frattali e che forniscano un test per l'esistenza di una genuina omogeneità. La conseguenza è che il clustering delle galassie mostra ben definite proprietà frattali con dimensione D=2. Queste proprietà si estendono fino ai limiti delle presenti osservazioni e dimostrano anche che l'assunzione di omogeneità non appare supportata dalle proprietà intrinseche del sistema. Questi risultati hanno notevoli implicazioni e dimostrano come l'invarianza di scala sia una proprietà concettualmente sottile e non intuitiva. La nuova prospettiva, ottenuta a partire dagli stessi dati osservativi ma con una metodologia più generale, cambia infatti radicalmente le conoscenze sulle proprietà a larga scala dell'Universo.
Origine delle strutture frattali
Rendersi conto che certe strutture in natura hanno proprietà frattali non spiega perché questo accada, ma è fondamentale per formulare le domande appropriate. L'impatto dei frattali in fisica, e in generale nelle discipline scientifiche, può essere descritto a tre diversi livelli di comprensione. (a) La geometria frattale come nuova matematica che conduce a un'inedita analisi di fenomeni e di dati noti, producendo spesso un sovvertimento di punti di vista consolidati. Questo permette di includere nelle aree scientifiche molti fenomeni caratterizzati da irregolarità intrinseche, finora trascurati a causa della mancanza di metodi matematici appropriati; (b) la formulazione di modelli fisici per sistemi che mostrano proprietà frattali e di autoorganizzazione. Da un punto di vista matematico spesso questi modelli sembrano relativamente semplici e consistono in processi iterativi non lineari, che però danno luogo a strutture con caratteristiche e proprietà estremamente complesse, generate spontaneamente dalla dinamica del sistema. Le simulazioni numeriche rappresentano uno strumento essenziale per esplorare queste proprietà e la maggior parte di esse è basata su modelli fortemente idealizzati e utilizzati a volte come semplici metafore. Esempi particolarmente rilevanti di modelli fisici di crescita frattale sono il DLA (Diffusion limited aggregation) e il DBM (Dielectric breakdown model): sono basati su una probabilità di crescita definita dalle soluzioni dell'equazione di Laplace e pertanto hanno validità molto generale, anche per fenomeni apparentemente diversi. Un esempio di strutture generate da questi modelli è dato dalla fig. 5; (c) la costruzione di teorie fisiche complete che permettano di capire l'origine autoorganizzata delle strutture frattali e delle altre proprietà dei sistemi fisici complessi. Una delle principali difficoltà è rappresentata dal fatto che la dinamica temporale è intrinsecamente irreversibile, difficoltà che non può essere aggirata facendo uso di ipotesi di tipo ergodico. Nella meccanica statistica dell'equilibrio, l'ipotesi ergodica permette infatti di eliminare l'evoluzione dinamica specifica e di assegnare direttamente un peso statistico (probabilità) di Boltzmann a una data configurazione. Nel caso delle strutture frattali questo normalmente non è possibile ed è necessario conoscere la storia completa del sistema per poter definire il peso statistico di una data configurazione.
Frattali nei fenomeni caotici e turbolenti
Un ambito che ha dato luogo a una nuova visione e a nuovi concetti è quello del caos deterministico, che ha importanti connessioni con le strutture frattali.
Il problema nasce dallo studio delle proprietà asintotiche di sistemi dinamici descritti da equazioni differenziali non lineari. Data la difficoltà dello studio diretto delle equazioni si è considerato il problema semplificato di processi iterativi discretizzati, come per esempio la mappa logistica
[6] xn+1=4λxn(1−xn)
con 0〈λ〈1. Anche la variabile x è definita nell'intervallo [0,1] e l'indice n rappresenta la dinamica evolutiva discreta. Per piccoli valori di λ si può osservare una convergenza verso l'attrattore x=0, indipendentemente dal valore iniziale di x. Aumentando λ si comincia a ottenere un valore finito per il punto di attrazione finché a un certo punto il sistema cade in un'orbita periodica che consiste nell'alternarsi di due ben definiti valori di x. Questo fenomeno è detto biforcazione e aumentando ancora λ oltre un certo valore caratteristico λc l'attrattore risulterà costituito da un numero infinito di punti. David Ruelle lo ha definito attrattore strano.
Si può però notare che i punti dell'attrattore, sebbene siano infiniti, non coprono l'intero intervallo [0,1] su cui l'iterazione è definita ma solo un suo sottoinsieme e possiedono inoltre proprietà frattali. Il fenomeno che osserviamo al valore λc viene chiamato transizione verso il caos poiché, pur essendo il processo deterministico, la sua evoluzione è così complessa da perdere ogni aspetto di predicibilità rispetto alle condizioni iniziali. Lo studio di questo tipo di iterazioni porta a pensare che la natura di queste transizioni verso il caos possa avere aspetti di universalità e quindi caratterizzare anche la dinamica di equazioni molto più complesse.
Il processo iterativo si può generalizzare anche al caso del piano complesso. Considerando la variabile z=a+ib, possiamo definire l'iterazione
[7] zn+1=z2n+c.
Assumendo c=1 e studiando questa dinamica a partire da vari punti del piano complesso possiamo osservare due tipi di evoluzione. Per alcuni punti il processo diverge all'infinito, per altri converge a un valore finito. L'insieme dei punti del piano complesso a partire dai quali il processo resta limitato si chiama insieme di Mandelbrot e corrisponde all'area in nero della fig. 6. Al di fuori di questa figura i vari colori danno un'idea della velocità con la quale l'iterazione diverge all'infinito nelle altre zone. Le proprietà frattali di queste strutture sono evidenti e dimostrano come un'iterazione non lineare estremamente semplice possa dar luogo a strutture di grande complessità.
Un esempio di equazioni non lineari apparentemente elementari che danno origine a comportamenti complessi e frattali è quello delle equazioni di Navier-Stokes, che descrivono il moto turbolento dei fluidi. Un parametro importante in esse è il numero di Reynolds: per alcuni suoi valori il fluido si comporta in modo laminare mentre per altri appaiono dei vortici che possono essere interpretati come singolarità nella distribuzione delle velocità.
Nel regime di turbolenza completamente sviluppata, ogni vortice è frammentato e composto a sua volta da vortici più piccoli e così via. Lo studio delle proprietà del campo delle velocità in regime turbolento è stato iniziato da Andreij Kolmogorov nel 1941 e la questione rappresenta ancora per molti versi un problema aperto. L'idea attuale è che l'energia immessa nel fluido in modo omogeneo a grandi scale viene dissipata in uno spazio frattale o multifrattale rappresentato dalla cascata dei vortici. Questa cascata inversa fu ipotizzata per la prima volta da Lewis F. Richarson.
Un semplice esperimento
Si può pensare che per generare sperimentalmente strutture complesse o frattali sia necessario un procedimento molto complicato. È vero esattamente il contrario. Queste possono essere generate in modo estremamente semplice e l'esperimento seguente dimostra che le strutture frattali sono spesso sotto i nostri occhi in ogni momento. Consideriamo un semplice foglio di carta: la sua dimensione è D=2. A volte per gettarlo via vogliamo renderlo più compatto e lo accartocciamo fino a formare una pallottola. Questo gesto molto frequentemente produce in realtà una struttura frattale con dimensione D=2,5. Se pensiamo a ciò che avviene in questo semplice processo, ci accorgiamo che è molto complesso da descrivere matematicamente. Il punto di partenza è una superficie che mantiene le sue proprietà topologiche, poiché la carta non viene strappata. Essa viene però ripiegata su se stessa in modo casuale e si genera chiaramente una condizione di volume escluso, come avviene nel caso dei polimeri. Ebbene, questo processo casuale di tale apparente semplicità produce una struttura frattale con dimensione ben definita e riproducibile.
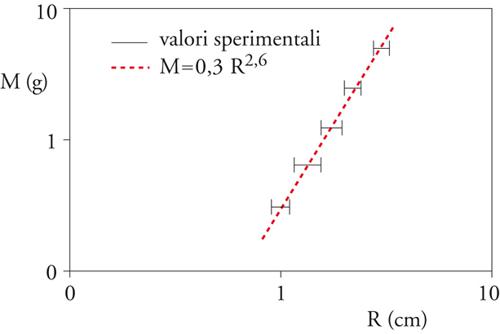
Per convincersene sperimentalmente si può utilizzare un foglio di alluminio da cucina, più stabile rispetto alla carta. Partendo da fogli di diversa area (massa), possiamo accartocciarli utilizzando la stessa forza, per esempio quella di una mano. Poi possiamo esaminare la dimensione (diametro) di queste strutture e possiamo cercare di definire una relazione massa-lunghezza del tipo
[8] M∝LD.
Nel grafico mostrato nella fig. 7 e nel relativo istogramma riportiamo in scala logaritmica i valori della massa e del diametro di queste strutture. L'andamento lineare del grafico avvalora l'esistenza di una legge di potenza del tipo della [1] e dalla sua pendenza possiamo stimare la dimensione frattale. Nel caso in questione prendiamo in considerazione solo cinque oggetti, ottenendo D=2,6 con un certo margine di errore (misure molto più accurate dimostrano che in realtà D=2,5). Il risultato è quindi che una pallottola di carta o di alluminio è in realtà una struttura frattale con dimensione ben definita e stabile rispetto a diversi materiali.
Bibliografia
Baryshev, Teerikorpi 2002: Baryshev, Yurij - Teerikorpi, Pekka, Discovery of cosmic fractals, Singapore, World Scientific, 2002.
Coleman, Pietronero 1992: Coleman, Paul H. - Pietronero, Luciano, The fractal structure of the universe, Amsterdam, North-Holland, 1992.
Cvitanovic 1984: Universality in chaos, edited by Predrag Cvitanovic, Bristol, Hilger, 1984.
Erzan 1995: Erzan, Ayse - Pietronero, Luciano - Vespignani, Alessandro, The fixed-scale transformation approach to fractal growth, "Review of modern physics", 67, 1995, pp. 545-604.
Evertsz 1996: Fractal geometry and analysis, edited by Carl J.G. Evertsz, Heinz-Otto Peitgen, Richard F. Voss, Singapore, World Scientific, 1996.
Gabrielli 2005: Gabrielli, Andrea e altri, Statistical physics for cosmic structures, Berlin, Springer, 2005.
Kadanoff 1990: Kadanoff, Leo P., Scaling and universality in statistical physics, "Physica A", 163, 1990, pp. 9-11.
Kadanoff 1993: Kadanoff, Leo P., From order to chaos, Singapore, World Scientific, 1993.
Mandelbrot 1983: Mandelbrot, Benoît, The fractal geometry of nature, New York, Freeman, 1983.
Paladin, Vulpiani 1988: Paladin, Giovanni - Vulpiani, Angelo, Anomalous scaling laws in multifractal objects, "Physics reports", 156, 1988, pp. 147-225.
Peebles 1993: Peebles, Phillip J.E., Principles of physical cosmology, Princeton, Princeton University Press, 1993.
Peitgen, Richter 1987: Peitgen, Heinz-Otto - Richter, Peter H., La bellezza dei frattali, Torino, Bollati Boringhieri, 1987.
Pietronero, Tosatti 1986: Fractals in physics, edited by Luciano Pietronero, Erio Tosatti, Amsterdam-New York, North-Holland, 1986.