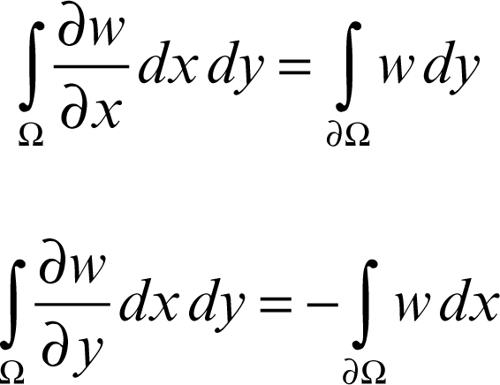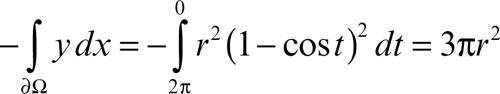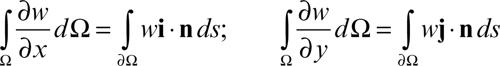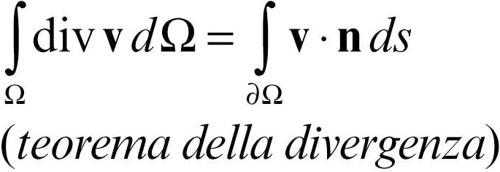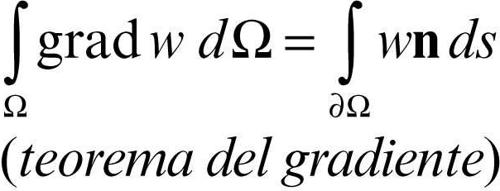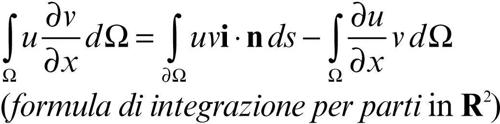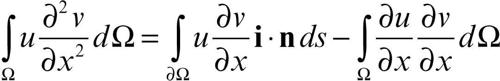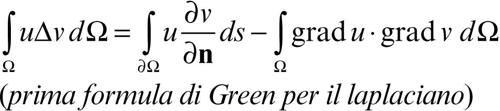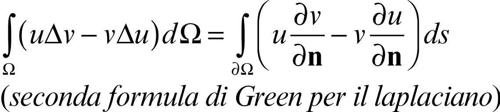Green, formule di
Green, formule di
Green, formule di o formule di Gauss o formule di Gauss-Green, in analisi, formule che trasformano un integrale esteso a un dominio nel piano o nello spazio in un integrale lungo la sua frontiera.
Nel caso bidimensionale, si consideri un dominio piano Ω, decomponibile in un numero finito di parti x- e y-convesse, la cui frontiera ∂Ω sia formata da una linea generalmente regolare percorsa in verso antiorario. Tali ipotesi possono essere indebolite e comunque sono soddisfatte da tutti i domini di uso pratico.
Se w(x, y) è una funzione di classe C1 in Ω̅, valgono allora le due formule
che consentono di calcolare gli integrali doppi a primo membro in integrali di forme differenziali lineari sulla frontiera. In particolare, se w = x o w = y si ottengono le formule per il calcolo dell’area
Ciò è molto utile quando ∂Ω è scritta in forma parametrica, per cui è difficile utilizzare le formule di riduzione per gli integrali doppi.
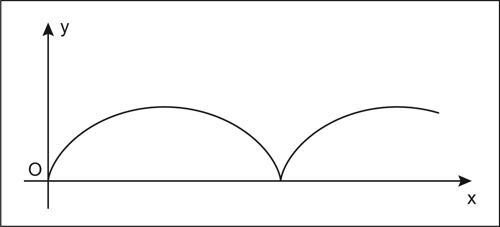
Per esempio, l’area del dominio Ω sotteso da un arco di cicloide, generata da un cerchio di raggio r e di equazioni parametriche x = r(t − sint), y = r(1 − cost), con 0 ≤ t ≤ 2π, è data dall’integrale
Il contributo all’integrale del segmento [0, 2π] dell’asse x, che delimita Ω dal basso, è nullo, mentre il verso di percorrenza dell’arco di cicloide è tale che la frontiera sia percorsa in senso antiorario.
Le formule di Green possono essere scritte anche nella forma seguente:
o anche in un’unica formula:
in cui compare la derivata direzionale di w rispetto a un generico versore r. In queste scritture n è la normale a ∂Ω uscente da Ω e s è l’ascissa curvilinea lungo ∂Ω.
Le formule continuano a valere se Ω è molteplicemente convesso e ∂Ω è formata da più linee, che devono essere percorse in modo da lasciare il dominio Ω alla sinistra. Corollari di queste formule sono per esempio:
Se Ω ⊆ R3, si possono scrivere le stesse formule, interpretando n come la normale alla superficie ∂Ω che forma la frontiera di Ω e sostituendo all’arco ds di linea l’area elementare dS.
